Применение тепловой теоремы Нернста к газовым системам

Как было отмечено выше, тепловая теорема относится к кон­денсированным системам. Непосредственно к газам она неприме­нима. В термодинамике принято считать, что газы подчиняются за­конам идеальных газов, а соотношения идеальных газов не удов­летворяют тепловой теореме. Так, например, для идеального газа

производная (dp/dT)_v = R/V при Т = 0 не обращается в нуль, в то время как по теореме Нернста она должна стремиться к нулю. Разность μс_р — μc_v = R при T = 0 для газов также не обращается в нуль, как это вытекает из тепловой теоремы.

Однако, как показал Нернст, выводы тепловой теоремы можно использовать для расчета констант равновесия газовых реакций, если проводить их условно та­ким образом, чтобы конечный результат был получен на базе взаимодействия промежуточных конденсированных состояний системы, к которым тепловую теорему применять можно.

Рассмотрим простейшую реакцию превращения газообразного вещества В в газообразное вещество Д при температуре Т = const. Начальные парциальные давления газов (рис. 46) будут Р_B и P_D, теплота реакции Q и максимальная работа газа А'_max.Проведем эту реакцию в три приема. Превратим газ В при Т = const и дав­лении Р_B в жидкое состояние В_ж. При этом выделится скрытая теплота испарения λ_B, на процесс конденсации затрачена работа А'_maxB Затем жидкое вещество В_ж превратим в жидкое вещество Д_ж, здесь выделится теплота Q_ж и будет произведена работа А'_maxж. После этого жидкое вещество Д_ж превратим в газообразное Д_г при Т = const и давление его доведем до начального P_D. При этом будет затрачена теплота λ_D на испарение и произведена работа А'_max д

Согласно первому и второму законам термодинамики теплота и максимальная работа реакции при изотермическом процессе не зависят от характера реакции. Поэтому для кругового изотерми­ческого процесса сумма работ и теплоты должна быть равна 0. Для суммарного процесса превращения вещества В_Г в вещество Д_г теп­лота Q_г и максимальная полезная работа могут быть определены как алгебраическая сумма теплоты и работ трех промежуточных стадий:

—Q_г= λB — Q_ж + λ_D; (256)

 

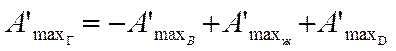(257)

Для нахождения работ А'_{max B} и А'_{max D} рассмотрим приведен­ные выше процессы в pVμ-координатах (рис. 47). При изотерми­ческом сжатии, соответствующем линии 1 — K, газ сжимается до состояния сухого насыщенного пара от объема и давление меняется от Р_в до р_в. В результате сжатия при изобар­ном процессе, соответствующем линии К — 2 газ В превращается

Рис. 47. Изменение пара­метров вещества при его конденсации (а) и испаре­нии (б) в рVμ- координатах

 

 

в жидкое вещество В_ж с объемом . Таким образом, если объемом жидкости пренебречь, то вся работа

.

Заменив из характеристического уравнения p_B V_μk на RT, по­лучим

.

Аналогично найдем работу испарения вещества D_ж и превраще­ния его в газообразное состояние р_г:

.

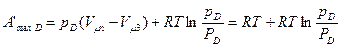Подставляя в уравнение максимальной работы (257) А'_B и A'_D, по­лучим

.

Согласно уравнению изотермы реакции (209) работу А'_{max г} можно представить в виде

.

Приравняем правые части полученных относительно А' _г уравне­ний:

Следовательно,

(258)

где А max _ж —максимальная работа, совершаемая при превращении жидкого вещества В_ж в жидкое вещество D_ж, а 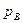и p_D — давле­ния насыщенных паров над жидкими веществами В_ж и D_ж, кото­рые определяются по уравнению упругости пара. Таким образом, исходя из положений тепловой теоремы получено уравнение, кото­рое можно применить для любых реакций между газами.

При нахождении К_р работа А'_maxж формуле определяется из соотношения (248), выведенного с учетом тепловой теоремы, а дав­ления р_в и p_D — из уравнения упругости пара в соответствии с уравнением (177)

где λ — теплота испарения; J' — константа интегрирования.

Константа интегрирования является величиной, характери­зующей данный газ и не зависящей от вида реакции. Ее обычно называют истинной химической константой.

20