При переходах индивидуального вещества из одного агрегатного состояния в другое каждому давлению соответствует определенная температура, при которой фазы находятся в состоянии термодинамического равновесия. Зависимость давления фазового перехода от температуры описывается уравнением Клапейрона—Клаузиуса, выведенном на основе второго закона термодинамики. Для вывода этого уравнения рассмотрим в р— vμ -координатах элементарный цикл, соответствующий площади 1-2-3-4 (рис. 30).
Предположим, что в точке f находится 1 кмоль рабочего тела, например жидкости. В процессе, соответствующем линии 1-2, при постоянном давлении подводится теплота и при постоянной




температуре происходит превращение жидкости в пар. Следовательно, процесс, соответствующий линии 1—2, является изобарно-изотермическим. Жидкость, превращаясь в пар, увеличивается в объеме от V'μ, в точке 1 до V''μ, в точке 2. В точке 2 вся жидкость превратится в пар. Парообразование происходит за счет подведенной теплоты Q1 , равной теплоте парообразования (r).
Пусть из точки 2 пар расширяется по адиабате до объема, соответствующего объему в точке 3, при незначительном изменении давления от р до (р—dp).. Температура при этом уменьшится от Т до (Т—dT). Затем при постоянных температуре (Т —dT) и давлении (р — dp) осуществим сжатие пара до объема, соответствующего точке 4. В точке 4 весь пар сконденсируется —превратится в жидкость.
Отводимая теплота в процессе, соответствующем линии 3—4, равна Q2 = Q1 — δQ.
Заменим процесс 4—1 адиабатным процессом 4'—1 перехода жидкости в состояние, соответствующее точке 1. Из-за малой величины dp изменением разности объемов (V"μ — V'μ) и (V3μ — V4μ,) можно пренебречь. Тогда цикл 1-2-3-4 превращается в элементарный цикл Карно 1-2-3-4', для которого справедливы равенства
δL = (V"μ — V'μ) dp
ηt = [Т — (T — dT)]/T = dT/T.
Так как термический КПД цикла Карно можно записать также в виде ηt = δL/Ql то, заменив в этом равенстве Q1 нa r и приравняв правые части полученных для ηt соотношений, можно записать
δL/r = dT/T
. Подставив вместо δL полученное значение, получим
[(V"μ — V'μ) dp]/r = dt/T
откуда
dp/dT = r/[T(V"μ — V'μ)]. (173)
Уравнение (173) называется уравнением Клапейрона—Клаузиуса. С помощью этого уравнения определяют давление или температуру при переходе индивидуального вещества из жидкого состояния в газообразное, а также объем (применительно к пару) и теплоту парообразования. Для любого другого фазового перехода вещества из одного состояния в другое в уравнении (173) следует заменить r на λ — теплоту фазового перехода (из различных фаз) в условиях равновесия. Тогда
dp/dT = λ/[T(V"μ — V'μ)] (174)
Уравнение Клапейрона—Клаузиуса (174) можно вывести и другим путем, исходя из равенства химических потенциалов при равновесии.
Как было показано ранее, условием равновесия двухфазной системы (при одинаковых давлении и температуре обеих фаз) является равенство их химических потенциалов (см. рис. 25), т. е. μ' = μ", где μ' и μ" — химические потенциалы индивидуального вещества соответственно в первой и во второй фазах.
Так как для однокомпонентной системы химический потенциал равен киломольной энергии Гиббса μ = G/n, то условие равновесия можно записать в виде dG'/dn' = dG"/dn".
Учитывая что уменьшение количества вещества в одной фазе должно равняться увеличению его в другой фазе, условие равновесия можно также записать в виде равенства энергий Гиббса в первой и во второй фазах, т. е. dG' = dG". Выразив dG' и dG" через соответствующие параметры (110), получим
V'μdp - S'dT = V''μdp - S"dT.
Откуда
dp/dT = (S'' - S')/ (V"μ — V'μ)
Учитывая, что приращение энтропии равно ΔS = ΔQ/T, и заменяя в полученном уравнении теплоту, подводимую на участке процесса перехода вещества из одной фазы в другую через λ, получим уравнение Клапейрона—Клаузиуса (174):
dp/dT = λ/[T(V"μ — V'μ)].
При рассмотрении процесса парообразования объемом жидкости V'μ можно пренебречь вследствие малости его по сравнению с объемом пара V"μ. Тогда уравнение (174) можно записать в виде
dp/dT=λp/T V"μ (175)
Если при этом заменить объем пара из уравнения Менделеева— Клапейрона (2) на RT/p, то уравнение Клапейрона—Клаузиуса будет иметь вид
dp/dT = λp/RT2
или, перенеся р в левую часть равенства и заменив dp/p на d (ln p), получим
d (In p)/dT = λ/RT2. (176)
Откуда
 (177)
(177)
где С = const.
Если сделать еще одно допущение, т. е. принять, что λ не зависит от температуры (λ = const) и проинтегрировать уравнение (177), то для небольшого интервала температур приближенная зависимость давления от температуры имеет вид
lg р = — λ/2,303RТ + С
или
 (178)
(178)
где С = const.
Таким образом, по формуле (178) с достаточной для практики точностью можно определить теплоту парообразования (или другого фазового перехода) по известным р1 и р2, соответствующим им температурам T1 и Т2 при небольшом их перепаде.
Уравнение (173) Клапейрона—Клаузиуса характеризует фазовые переходы, сопровождающиеся поглощением или выделением теплоты. Такие переходы обусловлены равенством энергии Гиббса двух находящихся в равновесии фаз и скачкообразным изменением первых ее производных, т. е. объема V = (дG/дp)T и энтропии S = - (дG/дp)р.
Эти переходы называются фазовыми переходами первого рода (к ним относятся испарение и конденсация, плавление и кристаллизация) и, следовательно, уравнение Клапейрона—Клаузиуса отражает особенности перехода первого рода.
12
Кроме фазовых переходов первого рода существуют также фазовые переходы второго рода. Впервые представления о переходах второго рода высказал Эренфест, объясняя явления перехода гелия из одного состояния в другое.
Для переходов второго рода характерным является отсутствие выделения и поглощения теплоты и, как следствие, равенство объема и энтропии сосуществующих в равновесии фаз. Для этих переходов характерно также скачкообразное изменение вторых производных энергии Гиббса, которыми являются такие физические величины, как теплоемкость
μcp = - T(д2G/дT2)p
коэффициент термического расширения

и коэффициент сжимаемости
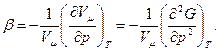
Фазовые превращения второго рода происходят при переходе обычных металлов с сверхпроводники, при превращении жидкого гелия из НеI в НеII (рис. 31). Тройная точка у гелия отсутствует.

ХИМИЧЕСКОЕ РАВНОВЕСИЕ






