Зависимость химического потенциала от давления и температуры

Выразим энергию Гиббса в функции от Т и р. Подставим в урав­нение G = H —TS вместо величин H и S их значения, выраженные через Т и р. Из уравнения (16) находим

Определим dS из уравнения (88):

dS = 1fT (dU + pdV) (140)

Здесь dU = μc_VdT, a pdV найдем из характеристического уравне­ния, предварительно продифференцировав его:

pdV_μ + V_μdp=R dT,

откуда

pdV_μ = RdT – V_μ = RdT – V_μdp = RdT – RTfp dp.

Подставляя полученные выражения в уравнение (140), имеем

После интегрирования

где 5°—энтропия вещества в состоянии, принимаемом за стан­дартное. Окончательно получим

(141)

Для отдельного компонента газовой смеси

G_i⁰ = G_i(T) + RTlnp (142)

а так как (135) G_i⁰ = μ_i, то химический потенциал i-го компонента смеси идеальных газов можно представить в виде

μ_i = μ_i(T) + RTlnp_i, (143)

где p_i — парциональное давление i-гo газа; μ_i (T) — часть хими­ческого потенциала, зависящая от температуры (и от природы газа).

Можно химический потенциал выразить также через концен­трацию i-гo компонента; для этого нужно заменить р_i на его зна­чение, выраженное через концентрацию. Из характеристического

уравнения p_iV = n_iRT находим p_i = n_ifV_i RT = C_iRT,

где C_i = n_ifV_i — киломольно-объемная концентрация; n_i V_i — соответственно число киломолей и объем компонента смеси. Тогда

μ_i = μ_i(Т) + RT In С + RT In (RT)

или, включив величину RT In (RT), представляющую собой функ­цию от температуры, в состав величины μ_i(T) и обозначив μ_i(Т) + RT In (RT) через 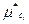(T), получим

(144)

 

Если в уравнение (143) подставить значение парциального давления, выраженное через объемную долю p_i =r_iр, то уравнение будет иметь вид

μ_i= μ_i^*(T) + RT In r_i + RT In p. (145)

 

Объединив в уравнении (145) члены, зависящие от температуры и давления, и обозначив сумму через μr_i (T, р), получим зависи­мость химического потенциала i-го газа, выраженную через объемные доли в виде

μ_i = μ_r (Т,р) + RTlnr_i. (146)

Аналогично, заменив p_i на n_ipfn (так как V_ifV = n_ifn), имеем

Объединив в этом выражении члены, зависящие от температуры и от объема

μ_i(Т) + RT ln RTfV= (T, F), получаем

μ_i = (T,V) + RT ln n_i. (147)

 

ФУГИТИВНОСТЬ И АКТИВНОСТЬ

Приведенные уравнения, как было обусловлено выше, спра­ведливы для идеальных газов. Для реальных же газов они не при­годны.

Однако, по предложению Льюиса (1901 г.) распространился метод использования этих уравнений для реальных газов при вве­дении в них термодинамических величин: фугитивности (или лету­чести) f и активности а, первая из которых характеризует давле­ние, а вторая — концентрацию. Под фугитивностью (или лету­честью) подразумевают термодинамическую величину данного газа, взятого отдельно, или в составе газовой смеси, являющуюся функцией температуры, давления и состава газовой смеси и обла­дающую тем свойством, что отношение значений ее для различных состояний этого газа при Т = const связано с соответствующими значениями его химического потенциала соотношением

(148)

 

а абсолютное ее значение определяется равенством

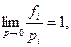
где р —общее давление; p_i —парциальное давление газа i, определяемое через киломольную его долю:

p_i = r_iр.

Размерность фугитивности совпадает с размерностью давления. Фугитивность идеального газа равна его давлению (f = p).

Таким образом, для реальных газов и их смесей будут спра­ведливы термодинамические соотношения идеального газа для изотермических процессов при замене в них давлений соответствую­щими значениями фугитивности.

Например, химический потенциал i-гo компонента смеси ре­альных газов можно представить в виде

μ_i = μ_i(T) + RT ln f_i

или максимальную полезную работу расширения реального газа в виде

(149)

Следовательно,

ΔG = G_i – G_i⁰ = (150)

 

Применение фугитивностей оказалось удобным в связи с тем, что были найдены способы определения их через параметры, ко­торые сравнительно легко измерить. Например, для случая, когда можно считать, что реальный газ отличается от идеального незначительно, фугитивность может быть определена по соотно­шению

f/p = p/p_ид

 

где р —давление газа; р_ид —давление газа, принятого за иде­альный, р_ид = RT/V_μ при заданных Т и V_μ.

Отношение фугитивности к давлению идеального газа назы­вается коэффициентом фугитивности γ, показывающим степень отличия газа от идеального:

γ = f/p_ид.

При исследовании термодинамических свойств реальных га­зов с помощью фугитивностей принято пользоваться их значе­ниями для газов в стандартном состоянии. Стандартным состоя­нием принято считать такое состояние идеального газа, фугитив­ность которого при данной температуре равна единице, а энталь­пия равна энтальпии реального газа при той же температуре и давлении, равном нулю. Изменение энергии Гиббса можно пред­ставить в виде

ΔG = G – G⁰ = =RT ln f, (151)

так как для стандартного состояния f ⁰ = 1.

Другой термодинамической величиной, которую принято под­ставлять в уравнения, связывающие свойства реального газа яв­ляется активность. Различают абсолютную и относительную тер­модинамические активности (последнюю принято называть просто активностью).

Абсолютная активность является безразмерной величиной, определяемой для вещества i в данной фазе (растворе) равенством

In λ_i = μ_i/RT, (152)

 

где μ_i — химический потенциал i-гo вещества при данной темпера­туре.

Относительная термодинамическая активность является без­размерной величиной, определяемой для i-гo вещества в данной фазе равенством

a_i = λ_i/λ_i⁰ (153)

или

In a_i = (μ_i — μ_i⁰)/RT. (154)

Относительная активность также зависит от концентрации каж­дого из веществ, содержащихся в фазе, от температуры и давле­ния. Для стандартного состояния а_i⁰ = 1. При подстановке зна­чений активности вместо значений концентрации в уравнения, выражающие связь различных термодинамических свойств идеаль­ного газа с его концентрацией, возможно применение этих уравне­ний к реальному газу.

Из уравнения (148) активность можно выразить через фугитивности:

a_i = f_i/f_i⁰. (155)

Так как для газов f_i⁰ = 1, то, следовательно,

a_i = f_i.

Подставляя в уравнение (144) значение активность вместо значе­ния концентрации, получим соотношение для химического потен­циала в виде

μ_i = μ_ia_i (T) + RT ln a_i (156)

или, подставляя значение активности вместо значения фугитивности в уравнение (150), получим уравнение энергии Гиббса

G_i – G_i⁰ = RT ln a_i. (157)

Отношение величины активности компонента к величине, характе­ризующей концентрацию компонента в данной газовой смеси, называют коэффициентом активности

φ_i = a_i/r_i, (158)

где r_i — объемная или мольная доля.