Термодинамические потенциалы

Термодинамическим потенциалом называется характеристиче­ская функция, убыло которой в равновесном процессе, протекаю­щем при постоянном значении соответствующих параметров, равна максимальной полезной работе, произведенной системой. Макси­мальная полезная работа А'_mах равна максимальной работе A_mах за вычетом работы против сил внешнего давления.

Рассмотрим эти потенциалы. Воспользуемся объединенным уравнением первого и второго законов термодинамики в общем виде для обратимого процесса, в котором полная работа будет максимальной:

TdS = dU + δA_max = dU + pdV + δA’_max. (114)

Если за независимые переменные принять S и V, то уравнение (114) примет вид

-dU = δA'_max

или

-ΔU= А'_mах, (115)

т. ё. уменьшение внутренней энергии в обратимом процессе при S и V — const равно максимальной полезной работе δA_mах = δA’_max, следовательно, внутренняя энергия является термодина­мическим потенциалом.

Приняв за независимые переменные S и р, из уравнения (114) получим

— (dU + pdV) = δA’_max или —d (U + pV) = δA'_max.

Заменив (U + pV) на H, после интегрирования имеем

-ΔH= А'_{max p} (116)

т. е. уменьшение энтальпии в обратимом процессе при S = const и р = const равно максимальной полезной работе процесса. Следо­вательно, энтальпия является также термодинамическим по­тенциалом.

Определим работу при независимых переменных V и Т. За­пишем объединенное уравнение первого и второго законов термо­динамики для обратимого процесса в виде

TdS =dU + δА_max,

откуда

-(dU - TdS)= ;

-d(U-TS)= .

После замены (U—TS) на E и интегрирования получим

-ΔF = , (117)

откуда следует, что уменьшение энергии Гельмгольца в обратимом

изохорно-изотермическом процессе равно максимальной работе.

Приняв за независимые переменные р и Т из объединенного

уравнения первого и второго законов термодинамики, получим

— (dU + pdV — T dS) =

или

-d(U + pV-TS) = .

Заменив (U + pV) на H, а (H — TS) на G, имеем

—dG =

или

-ΔH = , (118)

откуда следует, что уменьшение энергии Гиббса в обратимом изобарно-изотермическом процессе равно максимальной полезной ра­боте .

Из уравнений (102) и (110) следует, что в обратном изотермиче­ском процессе изменения энергии Гельмгольца в энергии Гиббса для 1 кмоль газа

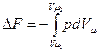
и

Заменив в этих выражениях р и V_μ из характеристического урав­нения Менделеева—Клапейрона

pV_μ = RT на соответствующие значения, получим изменение энергий Гельмгольца и Гиббса, а следовательно, и максимальной полезной работы в зависимости от давления и объема для изотермического процесса:

Из уравнений (119) и (120) следует, что при изотермическом про­цессе для идеального газа изменения энергии Гельмгольца и энергии Гиббса одинаковы, т. е. ΔF = ΔG.

 

§ 7. УРАВНЕНИЯ ГИББСА—ГЕЛЬМГОЛЬЦА

Заменив в уравнениях (101) и (109) значение 5 через производ­ные характеристических функций F и G для двух состояний газа и вычитая одно уравнение из другого, получим приращение энер­гии Гельмгольца и энергии Гиббса в виде

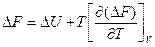(121)

и

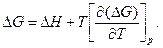(122)

 

 

Уравнения (121), (122), связывающие энергию Гельмгольца и энергию Гиббса с их производными по температуре для процес­сов при V и Т = const и р и Т = const, называются уравнениями Гиббса—Гельмгольца.

заменив ΔF и ΔG на и , на Q_v и ΔH на Q_p и поменяв у всех членов знаки на обратные, уравнения Гиббса Гельмгольца можно записать в следующем виде:

В табл. 3 приведены характеристические функции и их про­изводные.

 

Таблица 3 Характеристические функции и их производные

Независи­мые пере­менные	Характери­стические функции	Выражения для работы через харак­теристические функции	Частные производные х ар актеристических функций	Соотношения между частными производными параметров
V, S	Внутренняя энергия U
p,S	Энтальпия H = U + pV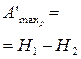
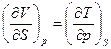
Т, V	Энергия Гельмгольца (изохорно-изотермический потенциал) F = U — TS
p, Т	Энергия Гиббса (изобарно-изо-термический потенциал) G = H — TS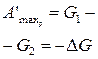

 

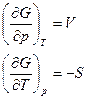
ХИМИЧЕСКИЙ ПОТЕНЦИАЛ

При рассмотрении взаимосвязи между термодинамическими потенциалами и параметрами системы предполагалось, что масса системы неизменна. И тогда для определения состояния системы достаточно было принять две независимые переменные величины. Если же в системе изменяется состав компонентов или вещество переходит из одной части системы в другую (что имеет место при химических реакциях или при изменении агрегатного состояния), то для определения состояния всей системы необходимо рассматри­вать каждую ее часть в отдельности, а в число независимых пере­менных включать еще состав смеси.

Термодинамические потенциалы каждой части такой системыf могут быть представлены как функции двух переменных и числа киломолей всех веществ, входящих в систему. Например, энер­гия U =f (S, V, n_l, n₂,..., n_k) или G = f (p, Т, n₁, n₂,..., n_k). Предположим, что при изменении числа киломолей какого-ни­будь вещества на dn₁ значение энергии Гиббса изменится на беско-

нечно малую величину 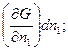изменение числа киломолей других компонентов также повлечет за собой изменение энергии Гиббса на соответствующие величины.

Тогда полный дифференциал dG, согласно уравнению (110)

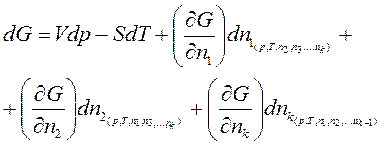(125)

 

Частные производные, входящие в уравнение (125), Гиббс (1875 г.) назвал химическими потенциалами. Гиббс химический потенциал относил не к одному киломолю, а к единице массы.

Химическим потенциалом каждого компонента называется частная производная энергии Гиббса по изменению числа киломолей, этого компонента (n_t) при неизменном числе киломолей всех остальных компонентов и при,р и Т = const.

Обозначим частные производные через μ_h тогда соответственно для первого, второго и i-го веществ

(126)

Тогда алгебраическая сумма произведений химического потен­циала каждого данного вещества на изменение числа киломолей этого вещества μ₁dn₁ + μ₂dn₂ +… μ_kdn_k

Следовательно, полный дифференциал энергии Гиббса (125) можно записать в виде

или

При условии протекания процесса (реакции) при р = const и Т = const получим

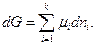(129)

Аналогичным образом можно выразить согласно (88), (95), и (102) полные дифференциалы других термодинамических потен­циалов, представляющих собой функции двух определенных не­зависимых переменных и числа киломолей веществ, входящих в систему.

Так, при V = const, 5 = const и n_l, n₂,..., n_k = const имеем

(130)

при р = const, 5 = const, n₂, n₃,..., n_k = const

(131)

при V = const, T = const и n₂, n₃,..., n_k = const

(132)

Нетрудно убедиться, что μ_i для каждого из веществ, входя­щих в термодинамическую систему, будет представлять собой частную производную от соответствующего термодинамического по­тенциала по изменению числа киломолей этого вещества при по­стоянных значениях определенных параметров системы и по­стоянных числах киломолей остальных веществ, т. е.

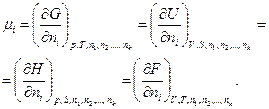(133)

Таким образом, из (133) следует, что химический потенциал мо­жет быть выражен через частную производную от любого термоди­намического потенциала (G, F, U, Н) при постоянных значениях соответствующих независимых переменных и числах киломолей всех веществ (кроме одного) по числу киломолей изменяющегося вещества, т. е. через парциальные значения этих потенциалов (отнесенные к киломолю вещества). Например:

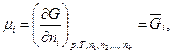(134)

 

где G_i — парциальное киломольное значение энергии Гиббса. Определить физический смысл химического потенциала можно, если проанализировать уравнения изменения термодинамиче­ского потенциала в общем виде, например изменение внутренней энергии из (114) и (125):

dU = TdS – pdV - δA'_max;

t=i

Здесь максимальную полезную работу δA'_max, если ее рассматривать как результат изменения состава смеси в процессе химиче­ского превращения, можно представить аналогично тому, как принято представлять количество энергии — в виде произведения двух физических величин — интенсивной и экстенсивной (9). Количество энергии, получаемое в форме механической работы, например, представляют как δL == pdV, а количество энергии, получаемое в форме теплоты, как

δQ = TdS, а в форме элект­рической энергии δA_ЭЛ = Ede.

В приведенных соотношениях р, Т и Е —интенсивные вели­чины — потенциалы механической работы, теплоты, электриче­ской работы соответственно, а V, S и е — экстенсивные величины.

В соответствии с уравнениями (114). и (125)

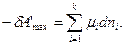
Здесь по аналогии μ_i — интенсивная величина — представляет собой потенциал химической работы, а n_i —экстенсивная вели­чина, количество кмоль превращающейся массы вещества.

Если системы (или части одной системы) с различными потен­циалами взаимодействуют между собой, то потенциалы выравни­ваются при изменении экстенсивных величин. Потенциалы, та­ким образом, являются движущей силой соответствующих про­цессов. Химический потенциал является движущей силой при хи­мических или фазовых превращениях — при перераспределении массы системы.

Потенциалы во взаимодействующих системах (частях системы) стремятся к выравниванию, приводящему систему к равновесию. Химический потенциал также по мере протекания химического процесса (или фазового превращения) выравнивается и становится одинаковым во всех частях термодинамической системы.

В общ м случае химический потенциал любого t-ro компонента является функцией состава системы и условий существования системы, например μ_i = f (p, T, n₁ n₂,..., n_k).

Для идеального газа или для смеси идеальных газов прини­мается, что химические потенциалы компонентов не зависят от их содержания в системе и для каждого компонента смеси идеаль­ных газов, находящихся при р — const и Т = const, химический потенциал равен значению энергии Гиббса, приходящейся на 1 кмоль компонента, взятого в стандартном состоянии, т. е.

μ_i = G_i⁰ = const. (135)

Для всей смеси идеальных газов энергия Гиббса

(136)

Продифференцировав полученное выражение, получаем

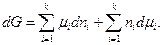(137)

Подставим в уравнение (137) вместо dG равное ему выражение из (110). После преобразований получим

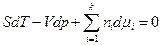(138)

 

Это уравнение называется уравнением Гиббса—Дюгема. При усло­вии протекания процесса при р и Т = const оно имеет вид

(139)