Направление реакции и мера химического средства

Из анализа выведенных уравнений изотермы химической реакции следует, что если значения начальных концентраций или парциальных давлений веществ соответственно равны равно­весным их значениям, то максимальные полезные работы A'_maxV или A'_maxp равны нулю. Это значит, что при равновесном состоянии не будет осуществляться в явном виде ни прямая, ни обратная реакция, т. е. система будет находиться в динамическом равно­весии.

Общее выражение зависимости константы равновесия от тем­пературы:

d In K/dT = Q/RT². (217)

Заменив натуральные логарифмы на десятичные и подставив значение универсальной газовой постоянной R, получим

d lg K/dT = Q /19,147 · 10³ T².

Из анализа полученных уравнений зависимости константы равновесия от температуры следует, что с повышением темпера­туры константа равновесия увеличивается в процессах, сопро­вождающихся поглощением теплоты (Q > 0), т. е. в эндотерми­ческих процессах. В экзотермических реакциях (т. е. когда Q < 0) константа равновесия при понижении температуры увеличи­вается.

В общем случае влияние на изменение химического равнове­сия различных факторов (главным образом температуры и давле­ния) подчиняется принципу смещения равновесия (принцип «Ле Шателье—Брауна»), рассмотренному выше.

§ 10. ВЫВОД УРАВНЕНИЙ ВИДА ln K = f(T) и А'_max = φ(T)

Уравнения изохоры и изобары химической реакции, получен­ные в дифференциальной форме, могут быть проинтегрированы, что позволяет получить зависимость вида ln К = f (Т), которая позволит определить константу равновесия при любых заданных температурах. В уравнении d In K/dT = Q/RT² для упрощения расчетов принимаем Q = const. Тогда после интегрирования

ln К = —Q/RT + С,

где С — константа интегрирования. Для небольшого темпера­турного интервала, где можно предположить, что Q не зависит (или мало зависит) от температуры, это уравнение может быть использовано для решения конкретных задач с точностью, при­емлемой для практических расчетов:

.

Заменяя натуральные логарифмы на десятичные и подставляя зна­чение R, получим

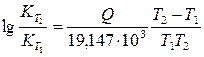(218)

 

Уравнение (218) дает возможность вычислить по данным значениям констант 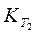, и 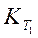в определенном температурном интервале значение теплоты реакции Q и, наоборот, рассчитать для этого интервала константу равновесия К₂, если известна теплота реакции и константа равновесия K₁.

Однако, как известно, теплота реакции также зависит от тем­пературы. Тогда в общем случае при подстановке вместо Q зна­чения Q = f (Т) уравнение константы равновесия как функции температуры К = f (T) принимает вид

d ln K/dT = Q/RT² = (Q₀ + αT + βT² + γT³)/RT²

или

d ln К = Q₀ dT/RT² + αdT/RT + βdT/R + γT dT/R.

Интегрируя, получим

(219)

 

где С — константа интегрирования.

Подставив в уравнение (219) значение R и переведя натураль­ные логарифмы в десятичные, получим

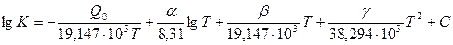. (220)

Уравнения (219) и (220) позволяют определить константу равно­весия, если известны Q₀ и константа интегрирования С. Однако определить константы интегрирования теоретическим путем, используя первый и второй законы термодинамики, невозможно, поэтому уравнение в таком виде решить не удается.

Для вывода уравнения A'_mах = φ(Т) воспользуемся уравне­нием константы равновесия (219) и работы в функции от темпе­ратуры (214).

Подставив в уравнение (214) значение ln К, получим урав­нение вида A'_max = φ(Т), т. е.

(221)

или, заменив A'_mах на ΔF⁰ или на ΔG⁰, a Q₀ на ΔU₀ или на ΔH₀,

(222)

и

. (223)

Уравнения (221)—(223), так же как и уравнение (219), дают воз­можность определить при данной температуре максимальную полезную работу реакции, изменение энергии Гельмгольца и энер­гии Гиббса (или меру химического сродства). При этом нужно знать также ΔU₀ и ΔH₀ и константу интегрирования С.

 

 

18