При термодинамических исследованиях, ориентированных на решение различных практических задач, определение направления и пределов течения процессов, может быть применен второй закон термодинамики и использована функция энтропия. Однако положения второго закона термодинамики и поведение функции 5 обычно рассматриваются в применении к изолированным системам. На практике приходится иметь дело с системами, взаимодействующими с окружающей средой и в этом случае для характеристики системы и выявления характера процессов, протекающих в ней, требуются другие функции. Такие функции и соответствующий метод исследования получены благодаря работам Гиббса, Максвелла, Масье, Гельмгольца и др. Эти функции называются характеристическими функциями (у Гиббса они называются фундаментальными).
Характеристической функцией называется функция состояния независимых параметров, характеризующаяся тем, что посредством этой функции и ее производных по этим параметрам могут быть выражены все термодинамические свойства системы.
К характеристическим функциям относятся: внутренняя энергия U, энтальпия Н, энергия Гельмгольца (изохорно-изотермический потенциал) F, энергия Гиббса (изобарно-изотермический потенциал) G и энтропия S.
Дифференциалы этих функций являются полными, функции аддитивны. Каждой функции соответствует вполне определенная пара постоянных параметров (если за независимые параметры принимать другие параметры, то данная функция от этих переменных не будет характеристической).
Метод исследования с помощью характеристических функций базируется на применении объединенного уравнения первого и второго законов термодинамики для обратимых процессов.
Из уравнений первого и второго законов термодинамики δQ = = dU + δА и dS = δQ/T можно получить следующие:
dS = (dU + δA)/T
или
 (86)
(86)
Если в системе совершается работа только против сил внешнего давления, то уравнения (86) примут вид
dS =(dU + pdV)/T (87)
или
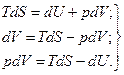 (88)
(88)
Уравнения (88) являются объединенными уравнениями первого и второго законов термодинамики. Каждое из этих уравнений связывает между собой пять переменных величин (Т, S, U, р и V), характеризующих состояние системы.
Если две из указанных величин принять за независимые переменные (например, Т и р или T и V), то в уравнении останется три неизвестных величины. Для решения вопроса о состоянии системы необходимо к написанному уравнению добавить еще два. Одно из этих уравнений может быть уравнением состояния f(р, V, Т) для идеальных газов —это pVμ = RT, а второе —какое-либо калорическое уравнение.






