Третий закон термодинамики

ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА

Полученные ранее уравнения Q = f (Т), ln К = f (T) и А'_max = φ (Т), являющиеся основными уравнениями химической тер­модинамики, позволяют рассчитывать тепловые эффекты реакции, определять условия химического равновесия и меру химического сродства. Однако для этого в зависимостях кроме теплового эффекта и теплоемкостей (Q₀ и μ c) необходимо знать постоянную интегрирования С. Эту величину теоретически с помощью первых двух законов термодинамики определить не представляется возможным.

Константа интегрирования может быть вычислена только в том случае, если экспериментально для соответствующей тем­пературы можно определить константу равновесия данной реак­ции. Необходимость предварительного нахождения константы равновесия для заданной температуры (что часто связано с боль­шими затруднениями) осложняло изучение равновесия химиче­ских реакций. Поэтому естественным было стремление исследова­телей найти способ определения константы интегрирования тео­ретическим путем.

Если графически построить в координатах Q_p—A^'_maxp = AG₀ и Т кривые функций

Q = f (Т) и —A'_maxp = ΔG = φ(T) по ранее приведенным уравнениям (56) и (223), получим

Q_p = Q₀ + αT + βT² + γT³

и

-A'_maxp = ΔG = Q₀ - αT ln Т - βT² - γТ³/2 - RTC,

то легко заметить, что при Т = 0 Q_p и —А_{mах р} = ΔG равны между собой, т. е. обе кривые будут выходить из одной точки К (рис. 45). Зависимость Q_p = f (T) изображается определенной кривой, начало которой расположено в точке К Отрезок на оси Q_p от нуля до точки К соответствует Q₀. Зависимость

—A'_{max р} — ΔG = φ(T) на графике, из-за неопределенности постоянной интегрирования С, не может быть изображена определенной кривой.

Соответственно различным значе­ниям С имеется целое семейство l кривых, берущих свое начало также из точки К

Вальтером Нернстом (1906 г.) была высказана гипотеза о том, что для конденсированных систем не только при абсолютном нуле, но и вблизи него значения энергии Гиббса и теплоты реакции Q_p

равны между собой, т. е. Q_p = f (Т) и ΔG = φ (T) при Т = 0, и не только выходят из одной точки К, но и вблизи абсолютного нуля имеют общую касательную. Следовательно, первые производные в точках касания, представляющие собой тангенсы углов наклона касательных к осям координат, должны быть равны между собой:

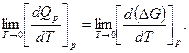
Экспериментально установлено, что при очень низких температу­рах свойства, конденсированных тел перестают зависеть от темпе­ратуры. Поэтому общая касательная кривых функций Q_p = f (T) и ΔG = φ (Т) должна идти параллельно оси температур:

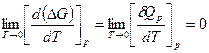
Для проверки этого предположения найдем из уравнений Гиббса— Гельмгольца (122) [ д (ΔG) д T]_p при Т → 0:

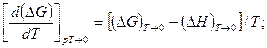(246)

при T = 0

ΔG=ΔG₀=ΔH_0.

Следовательно, в правой части данного уравнения получили не­определенность.

Для раскрытия неопределенности продифференцируем по Т в правой части уравнения (246) в соответствии с правилом Лопи-таля числитель и знаменатель дроби, тогда

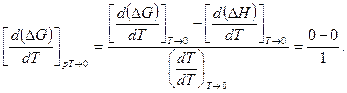
Таким образом,

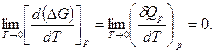(247)

Из большого семейства кривых, представляющих функцию ΔG =φ (T), искомой кривой будет кривая, касательная к которой проведенная через точку K, параллельна оси Т.

Тепловая теорема Нернста позволяет решать уравнения для конденсированных систем вида lg К_р = f (Т) и ΔG = φ (T) по тепловым эффектам реакций и теплоемкостям веществ, участвую­щих в реакции. С помощью теоремы Нернста можно определить константы интегрирования, неизвестные в указанных уравнениях.

Дифференцируя уравнение зависимости теплового эффекта Qp = f{T) от температуры (56) по температуре и учитывая, что Q₀ — const, получим

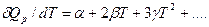
При T = 0 К α = δQ_p/dT. Так как {δQ/dT)_T=o = 0, то и α=0, следовательно,

δQ_p/dT = 2βT + ЗγТ² +….

Дифференцируя уравнение зависимости энергии Гиббса от температуры

ΔG == 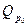— αT ln T — βT² — О,5γТ³ — RTC по температуре Т с учетом Q_P0 = const

и α=0, получим

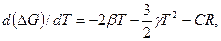
при Т=0

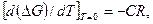
но так как 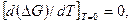то при Т=0 и CR=0. Однако R не может быть равно нулю, поэтому С = 0. Следовательно, в урав­нениях для конденсированных систем вида ΔG = φ (T) и In K_p = f (T) константы интегрирования равны нулю. Учитывая это, можно записать

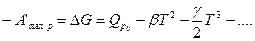(248)

 

Из (248) следует, что максимальная полезная работа и энергия Гиббса могут быть вычислены при любой температуре по тепло­вому эффекту и теплоемкостям реагирующих веществ.

Если принять, что теплоемкость зависит от температуры по линейному закону, то уравнения зависимости энергии Гиббса и энергии Гельмгольца от температуры будет иметь вид при V = const ΔF = -RT ln K_c = Q_Vo — βT²; при р = const ΔG = — RT ln и Kp = Q_Po — βT². Так как для кон- дейсйрованных систем различие между A'_maxp и A'_maxv невелико _То в общем виде

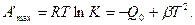(249)

Уравнение (249) можно получить также в другом виде для этого умножим обе части уравнения работы 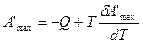на dT и разделим на —Т². Тогда

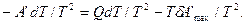
Перенесем в левую часть равенства член, содержащий ;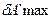

.

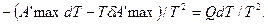Проинтегрируем и умножим на Т обе части равенства:

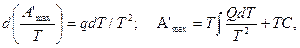
где С = 0 (согласно теореме Нернста) для конденсированной си­стемы. Следовательно,

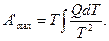
Имея в виду, что С = 0, и согласно закону Кирхгоффа,

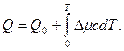
Подставив эти значения, получим

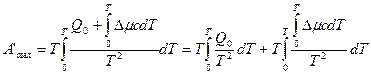
или

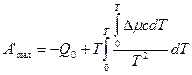. (250)

В такой форме удобно выражать работу, так как для многих реак­ций при разных температурах в таблицах приведены численные значения интегралов, входящих в уравнение (250).

ОСНОВНЫЕ СЛЕДСТВИЯ ТЕПЛОВОЙ ТЕОРЕМЫ НЕРНСТА

Из тепловой теоремы Нернста можно получить ряд важнейших следствий, имеющих большое практическое значение. Так, напри­мер, из уравнения Кирхгоффа (54) известно, что

δQ/dT = μс₂ — μс₁ = Δμс.

Согласно теореме Нернста (δQ/dT)_T→0 = 0. Следовательно, можно сказать, что при абсолютном нуле алгебраическая сумма теплоемкостей конденсированных систем равна нулю, т. е.

(251)

Это положение распространил Нернст и на значение самих теплоемкостей конденсированных систем. Это положение в настоя­щее время, как известно, подтвердилось в экспериментах: тепло­емкости твердых тел при температуре, близкой к 0 К, резко падают и стремятся к нулю.

Из тепловой теоремы Нернста можно получить еще одно важ­ное следствие, касающееся вычисления абсолютного значения энтропии.

Запишем уравнения максимальной работы (119) и (120) в диф­ференциальной форме:

 

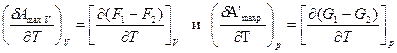
Учитывая, что 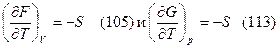, можно записать

В общем случае имеем

;

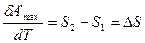при T=0

.

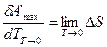Так как

,

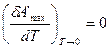то и

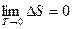. (252)

Следовательно, можно сказать, что при абсолютном нуле темпе­ратуры изменение энтропии конденсированных тел равно нулю.

В дальнейшем это следствие из теоремы Нернста было допол­нено Планком (1912 г.). Он предположил, что при температуре Т = 0 К значение энтропии конденсированных тел также можно считать, равным нулю, т. е.

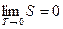. (253)

 

Это допущение носит название постулата Планка. Учитывая урав­нение (253), можно вычислять абсолютные значения энтропии S конденсированных тел в зависимости от температуры.

Допустим, например, что при данной температуре необходимо определить энтропию тела, изменяющего свое состояние при р = const. Запишем известное уравнение для приращения энтро­пии

dS = δQ/T.

Заменив δQ = μс_рdT, получим

.

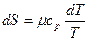Проинтегрировав полученное уравнение, определяем приращение энтропии:

.

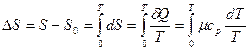Так как согласно постулату Планка S₀ = 0, то энтропия тела для данной температуры

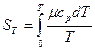. (254)

Таким образом, если известен закон изменения теплоемкости от температуры μс_р = f(T), то может быть найдено и истинное значение энтропии конденсированного тела для любой темпера­туры.