Внутренняя энергия и ее частные производные

Примем за независимые переменные V и S. Тогда внутренняя энергия будет функцией этих переменных V =f(V, S). Так как дифференциал внутренней энергии является полным дифференциалом, то

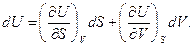(89)

Сравнив уравнения (88) и (89), можем записать

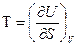(90)

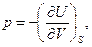(91)

т. е. через первые производные характеристической функции U (по переменным V и S) определяются недостающие параметры системы (90) и (91).

Вторая производная от V (S, V) дает следующее:

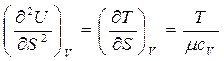
(так как 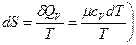, откуда теплоемкость при постоянном объеме

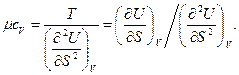(92)

Если уравнения (90) и (91) продифференцировать вторично по другой переменной, то

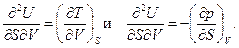
Поэтому

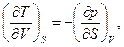(93)

Уравнение (93) связывает термические и калорические соотношения системы.

ЭНТАЛЬПИЯ И ЕЕ ЧАСТНЫЕ ПРОИЗВОДНЫЕ

Примем за независимые переменные р и S, тогда энтальпия будет функцией переменных

Н = f (p, S). Полный дифференциал этой функции

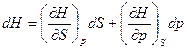(94)

Преобразуем объединенное уравнение (88). Прибавив к обеим частям равенства Vdp, получим

dU + Vdp = TdS —pdV + Vdp

или

dU + Vdp + pdV = TdS + Vdp.

Откуда

d (U + pV) = T dS + Vdp.

Так как U + pV = H, то уравнение можно записать в виде

dH = TdS + Vdp. (95)

Сравнивая уравнения (94) и (95), находим

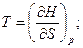(96)

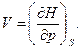(97)

Вторая производная от Н (S, р)

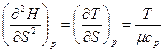
(так как dS = δQ_pfT = μc_pdTfT) откуда теплоемкость при постоянном давлении

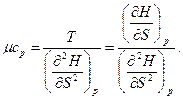(98)

Продифференцировав вторично уравнения (96) и (97) по другой переменной, получим

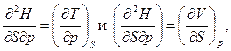
откуда получаем уравнение, связывающее термические и калорические соотношения

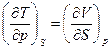(99)

или

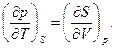(100)

Следовательно, через первые производные характеристической функции Н (S, р) определяются термические параметры системы по независимым переменным р и S, а через вторые — калорическая величина μc_p.

ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА

(ИЗОХОРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛ)

Примем за независимые переменные V и Т из обеих частей равенства объединенного уравнения первого и второго законов термодинамики, записанного в виде dU —TdS = —pdV. Вычтем из обеих частей равенства SdT:

—SdT + dU —TdS = —pdV —SdT,

откуда

d(U — TS) = —pdV — SdT.

Величина (U—TS) зависит от функций состояния U и S и, следовательно, она является также функцией состояния. Ее называют энергией Гельмгольца или изохорно-изотермическим потенциалом. Эта функция в переменных V и Т является характеристической функцией и обозначается буквой F:

F = U —TS. (101) (101)

Подставив F в полученное выше уравнение, можно записать

dF = —pdV —SdT. (102)

Так как эта функция обладает свойствами полного дифференциала, запишем его значение в частных производных по независимым переменным V и Т:

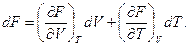(103)

Сравнивая уравнения (102) и (103), получаем термические параметры, выраженные через первые производные функции F по независимым переменным V и Т

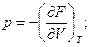(104)

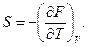(105)

Через вторую производную можно получить калорическую величину — теплоемкость μc_v, т. е.

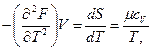
откуда

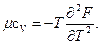(106)

Вторые производные по второй переменной

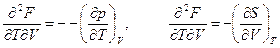
позволяют получить соотношение между термическими и калорическими величинами

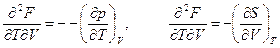
Если в уравнении (102) вместо члена — pdV (работы против сил внешнего давления) подставить внешнюю работу А, то получим

dF = — δА —SdT.

Потому для изотермического процесса (Т = const)

dF = —δА, (107)

а для изохорно-изотермического (V = const и Т — const)

dF == — δА’ = — δA, (108)

так как δA =δA' + pdV.

Таким образом, энергия Гельмгольца (F) является той частью внутренней энергии (F = U — Ts), которая может быть превращена во внешнюю работу А при обратимом изотермическом процессе или в работу против немеханических сил при изохорно--изотермическом процессе, взятых с обратным знаком.

Величина TS = U — F называется связанной энергией. При Т = const связанная энергия не может быть превращена в работу, а превращается только в теплоту.

ЭНЕРГИЯ ГЙББСА (ИЗОБАРНО-ИЗОТЕРМИЧЁСКИЙ ПОТЕНЦИАЛ)

Примем за независимые переменные р и Т. В объединенном уравнении вида

dU + pdV —TdS =0

прибавим к обеим частям равенства величину Vdp — S dT. Тогда

dU + pdV — TdS + Vdp — SdT = Vdp — S dT.

После преобразований имеем

d (U — TS + pV) = Vdp — SdT.

Заменив выражение в скобках на Н — TS, получаем

d (H — TS) = Vdp — SdT.

Величина Н—TS является функцией состояния; а переменные р и Т — характеристическими функциями. Функция состояния обозначается буквой G и называется энергией Гиббса или изобарно-изотермическим потенциалом:

G = H — TS. (109)

Заменив (H — TS) на G, можно записать

dG = Vdp —SdT. (110)

Дифференциал dG также будет полным. Представим его в частных производных по независимым переменным р и Т:

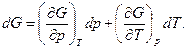(111)

Из уравнений (110) и (111) получим

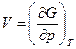, (112)

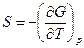(113)

Следовательно, по функции G через ее первые частные производные при независимых переменных Т и р можно определить недостающий параметр системы V и функцию S.