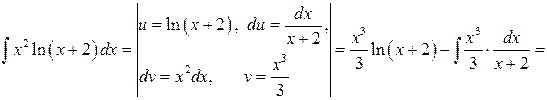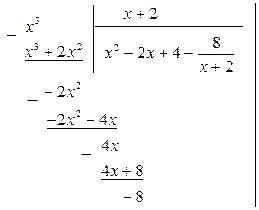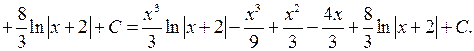Поняття невизначеного інтеграла
При диференціюванні задано функцію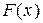 
і потрібно знайти її похідну 
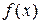, тобто в рівності
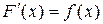(3.1)
функція 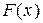відома, а 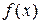треба знайти.
При інтегруванні невідома функція 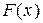, але відома її похідна 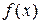. Таким чином, інтегрування – дія, обернена диференціюванню.
Якщо має місце рівність (3.1), то функція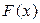 
називається первісною функції 
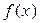. Ясно, що 
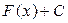, де 
- стала інтегрування, також буде первісною від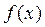 
. Можна довести, що інших первісних від 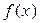немає, тобто 
є сукупність усіх первісних від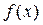 
.
Означення. Невизначеним інтегралом для неперервної функції 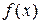називають множину всіх первісних функцій 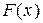і позначають
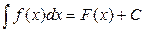. (3.2)
Основні властивості невизначеного інтеграла:
1) 
;
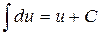2) 
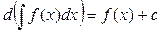
2) 
;
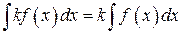3) 
.
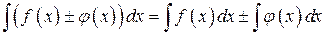Зауваження:
1) якщо 
, то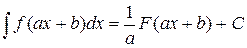 
.
2) якщо в чисельнику стоїть диференціал знаменника, то первісна такої функції дорівнює натуральному логарифму модуля знаменника
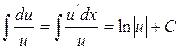(3.3)
Таблиця основних інтегралів
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
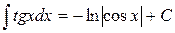
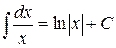
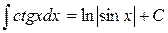
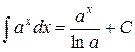
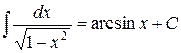
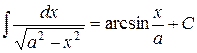
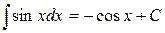
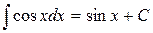
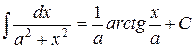
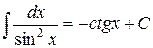
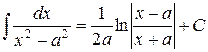
Частина цих формул (наприклад, 2, 4, 5, 6, 7, 11) є оберненими до формул таблиці похідних, інші отримані за допомогою певних прийомів інтегрування, частину з яких ми розглянемо нижче.
При інтегруванні застосовуються часто дві такі властивості невизначеного інтеграла, безпосередньо пов'язаних з його обчисленням
Безпосереднє інтегрування
Суть його складається в тому, що іноді вдається складну функцію або добуток функцій за допомогою деяких операцій або формул зводити до суми табличних інтегралів. Безпосереднє інтегрування виконується з використанням таблиці інтегралів і наведених властивостей.
Приклад 3.1. Знайти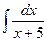 
 |
Розв’язання.
Приклад 3.2. Знайти інтеграл 
Розв’язання.
Тут почленним діленням інтеграл звівся до табличних 4 і 6.
Приклад 3.3. Знайти інтеграл 
.
Розв’язання.
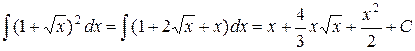
Звернемо увагу на те, що 
, 
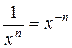, тому інтеграли від цих функцій обчислюються за формулою 1 таблиці інтегралів.
Приклад 3.4. Знайти інтеграл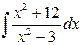 
.
Розв’язання. Виділимо цілу частину підінтегральної функції. Для цього поділимо чисельник на знаменник способом діленням многочлена на многочлен, або припишемо в чисельнику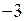 
та 
і розглянемо суму дробів. Одержимо
.
.
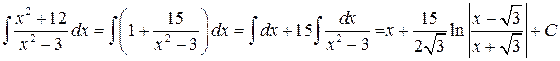9.4. Метод заміни змінної (метод підстановки)
Метод інтегрування підстановкою полягає у введенні нової змінної інтегрування (тобто підстановки). При цьому заданий інтеграл приводиться до нового інтеграла, що є табличним або до такого, що до нього зводиться (у випадку «вдалої» підстановки). Загальних методів підбора підстановок не існує. Уміння правильно визначити підстановку здобувається практикою.
Нехай потрібно обчислити інтеграл 
Зробимо підстановку х = φ (t), де φ (t) — функція, що має неперервну похідну.
Тоді dx = φ′ (t) dt і на підставі властивості інваріантності формули інтегрування невизначеного інтеграла отримуємо формулу інтегрування підстановкою
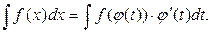(3.4)
Формула (3.4) також називається формулою заміни змінних у невизначеному інтегралі. Після знаходження інтеграла правої частини цієї рівності варто перейти від нової змінної інтегрування t назад до змінної х.
Іноді доцільно підбирати підстановку у вигляді t = φ (x), тоді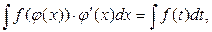 
де t = φ (x). Інакше кажучи, формулу (3.4) можна застосовувати праворуч і ліворуч.
Приклад 3.5. Знайти інтеграл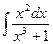 
Розв’язання
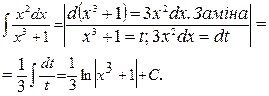
Приклад 3.6. Знайти інтеграл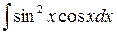 
.
Розв’язання
.
Можна також використовувати і такий запис:
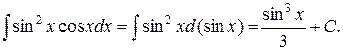
Приклад 3.7. Знайти інтеграл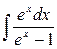 
.
Розв’язання. 
Приклад 3.8. Знайти інтеграл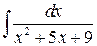 
.
Розв’язання. Виділивши повний квадрат у знаменнику підінтегральної функції, зможемо застосувати відповідну формулу із таблиці інтегралів. Одержимо
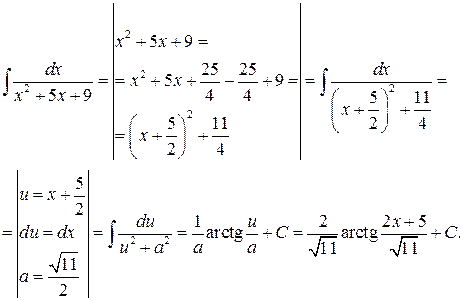
Приклад 3.9. Знайти інтеграл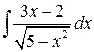 
.
Розв’язання. Розглянемо різницю двох інтегралів і до кожного із них застосуємо відповідну формулу із таблиці інтегралів. Одержимо 
,
.
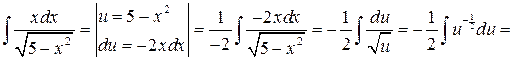
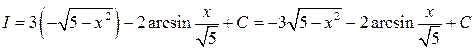Приклад 3.10. Знайти інтеграл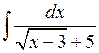 
.
Розв’язання. Часто доводиться вводити заміну для спрощення обчислення інтегралу. Замінимо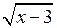 
на нову змінну. Одержимо
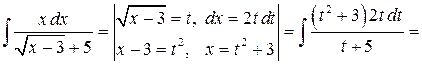
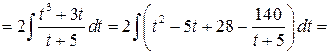
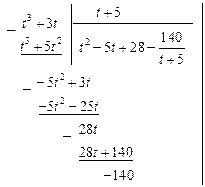
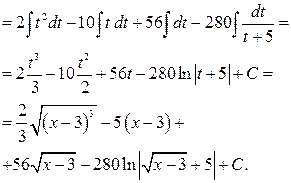
Зауваження. Метод заміни змінної можна використовувати й у деяких інших випадках. Вони будуть розглянуті далі.
Інтегрування частинами
Цим методом у деяких випадках вдається про інтегрувати добуток або частку функцій.
Формула інтегрування частинами має вигляд:
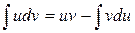(3.5)
Корисні такі рекомендації.
1. Якщо підінтегральна функція представляє собою добуток алгебраїчної функції на показникову або тригонометричну функцію, то проміжною змінною u треба позначати алгебраїчну частину.
2. Якщо підінтегральна функція представляє собою добуток алгебраїчної функції на логарифмічну або обернену тригонометричну функцію, то змінною u треба позначати неалгебраїчну частину.
Приклад 3.11. Знайти інтеграл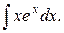 
Розв’язання. Відповідно до рекомендації 1 зазначимо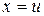 
. Щоб інтеграл прийняв вид 
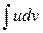, зазначимо 
.
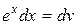Щоб скористатися формулою (3.5) треба знайти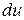 
і 
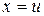, тому рівняння продиференціюємо, а в рівнянні 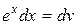знайдемо первісну. Будемо мати: 
, 
.
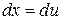За формулою (3.5) одержимо: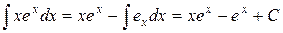 
Приклад 3.12. Знайти інтеграл 
Розв’язання. Рекомендація 1 нічого не дасть. Дійсно, якщо позначати ,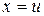 
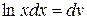, то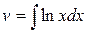 
. Цей інтеграл ми знайти не зможемо.
Скористаємося рекомендацією 2. Розв’язання можна оформити у такий спосіб:
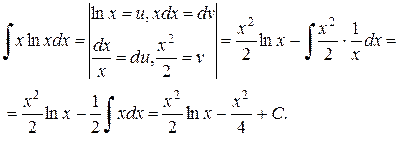
Зауваження. Іноді інтегрування частинами доводиться застосовувати в одному прикладі декілька разів.
Приклад 3.13. Знайти інтеграл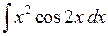 
.
Розв’язання.
Приклад 3.14. Знайти інтеграл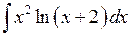 
.
Розв’язання. Для знаходження інтеграла застосуємо формулу (3.5). Одержимо
