К структурным характеристикам ряда распределения относят медиану и моду. Они не зависят от крайних значений вариантов, поэтому применяются для характеристики центра в ряду распределения с неопределенными границами.
4.2.1. Медиана (Me) - это значение признака, приходящееся на середину упорядоченной совокупности.
Её используют как наиболее надежный показатель типичного значения признака в неоднородной совокупности (включающей резкие отклонения от 
).
Медиана находит широкое практическое применение также вследствие особого математического свойства: сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:
Медиана (Ме) соответствует варианту, стоящему в середине ранжированного ряда.
Положение медианы определяется ее номером по формуле:
N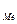 
= 
,
где:
n – число единиц в совокупности.
Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.
Численное значение медианы для интервального ряда определяется по формуле:
, где:
— нижняя граница интервала, в котором находится медиана;
— величина интервала;
— сумма накопленных частот интервалов, предшествующих интервалу, в котором находится медиана;
— частота интервала, в котором находится медиана.
4.2.2. Мода (Мо) – это варианта, соответствующая наибольшей частоте или варианте, которая встречается наибольшее количество раз.
В дискретном ряду мода определяется визуально по максимальной частоте (f) или частости.
В интервальном ряду модальный интервал определяется по наибольшей частоте, т.е. это тот интервал, который имеет наибольшую частоту, а конкретное значение моды в интервале вычисляется по формуле:
Мо = х0 + i 
, где:
Х0 –нижняя граница модального интервала,
i - величина модального интервала,
fM 
, fM 
, fM 
- частоты (частости) модального, предмодального и послемодального интервалов.
Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды.
Если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариант больше двух, то ряд – полимодальный.
Мода так же, как и медиана, не требует знания всех индивидуальных значений признака и поэтому может быть использована в качестве наиболее типичного значения признака в неоднородной совокупности.
На практике мода и медиана часто используются вместо средней арифметической или наряду с ней. Так, фиксируя средние цены на оптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т.е. определяют моду цены. Тем не менее, наилучшей характеристикой величины варианта служит средняя арифметическая, которая имеет ряд существенных преимуществ, главное из которых – точное отражение суммы всех значений признака, использующихся для решения соответствующих практических задач.
Решение типовых задач
4.3.1. За январь имеются следующие данные о заработной плате продавцов по четырем секциям торгового дома:
| секции | заработная плата, рублей x | количество продавцов f | фонд оплаты труда, рублей xi fi |
| Итого |
Вычислитесреднюю месячную заработную плату по четырем секциям в целом.
Решение:
Обозначим заработную плату через x, а количество продавцов через f. Логическая формула средней величины имеет следующий вид:
Средняя заработная плата = 
Фонд оплаты труда (ФОТ) каждой секции представляет собой произведение заработной платы на количество продавцов этой секции,
т.е. 
.
Чтобы определить ФОТ по всему торговому предприятию, необходимо исчислить фонды по каждой секции, затем их суммировать.
Средняя заработная плата одного продавца в целом по торговому предприятию за месяц будет равна отношению этой суммы и численности продавцов всех секций.
Так как ФОТ равен произведению варианты на частоту, то, в этом случае, для определения средней величины применяется формула средней арифметической взвешенной. Обоснованную логическую формулу выразим алгебраически через соответствующие обозначения:
= 
= 
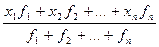, где:
x 
- ФОТ первой секции,
f1 - численность продавцов первой секции,
x2f2 - ФОТ второй секции,
f2 - численность продавцов второй секции и т.д.
Теперь произведем расчет средней заработной платы одного продавца по формуле средней арифметической взвешенной:
= = 
= 
= 25115 руб.
Средняя заработная плата одного продавца, рассчитанная по формуле средней арифметической взвешенной, за январь равна 25115 руб.
Какой экономический смысл заключается в формуле средней арифметической взвешенной?
В числителе вполне определенная величина: ФОТ; в знаменателе – численность всех продавцов. Отношение числителя и знаменателя дает среднюю величину. Важно подчеркнуть это обстоятельство для того, чтобы уяснить экономическую связь между реальными показателями и средней взвешенной величиной. Она связана с общим размером ФОТ: если среднюю величину 25115 руб. умножить на число продавцов 16, то должны получить общий размер фонда оплаты труда (25115*16=401840 руб.).
ФОТ – величина, которая является определяющим показателем и от которой зависят форма и величина средней величины.
4.3.2. По данным таблицы требуется определить средний процент студентов университета, направленных на обучение организациями:
| отделение университета | всего студентов, чел. | из них, направленные на обучение организациями, % |
| заочное | ||
| очное | ||
| Итого |
Решение:
Вариантами (х) в данном случае являются проценты направленных студентов на обучение организациями потребительской кооперации, а весами или частотами (f) – количество студентов на каждом отделении.
Средний процент направленных студентов на обучение кооперативными организациями в целом по университету равен:
= 
= 
= 
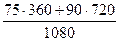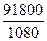= 85%
4.3.3. За два месяца по предприятиям района имеются следующие данные:
| № предприятия | сентябрь | октябрь | ||
| численность работников | средняя месячная заработная плата, руб. | средняя месячная заработная плата, руб. | фонд заработной платы, руб. | |
Определите, за какой месяц и на сколько процентов была выше средняя месячная заработная плата работников предприятия.
Решение:
Введем условные обозначения для сентября:
f - численность работников по каждому предприятию;
x - средняя месячная заработная плата работников каждого предприятия.
Определяющий показатель – общий фонд заработной платы - 
.
Средняя месячная заработная плата работников предприятия за сентябрь составила:
= = 
= 
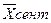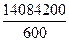= 23473,7 руб.
Условные обозначения для октября следующие:
w - фонд заработной платы по каждому предприятию;
x – средняя месячная заработная плата работников каждого предприятия.
Определяющий показатель - 
.
Средняя заработная плата в октябре исчисляется по формуле средней гармонической взвешенной:
где: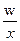 
- численность работников каждого предприятия в октябре.
Динамика средней месячной заработной платы работников предприятий:
или 100,3%.
Следовательно, средняя месячная заработная плата работников предприятий в октябре повысилась на 0,3% по сравнению с сентябрем (100,3% - 100%).
4.3.4. В таблице имеются данные о дневной выработке деталей рабочими цеха (графы 1-2):
| дневная выработка, шт. (х) | число рабочих (f) | среднее значение интервала (x  ) 
| произведение середины интервала на число рабочих (x  f)
|
| до 100 | 
| ||
| 100-120 |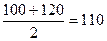 
| ||
| 120-160 | 
| ||
| 160 и более | 
| ||
| Итого: | - |
(в графах 3-4 данной таблицы уже выполнены предварительные расчеты для решения задачи).
Определите среднедневную выработку рабочих цеха.
Решение:
Так как предварительные расчеты уже сделаны в таблице, то среднедневную выработку рабочими цеха, находим по формуле средней арифметической взвешенной:
= = 
деталей
Следовательно, рабочие цеха делают в среднем 125 деталей в день.
4.3.5. Определитемоду по данным таблицы:
Распределение размеров женской обуви,
проданных в обувном отделе торгового объединения, в ноябре 2010 г.
| размер женской обуви (х) | число проданных пар, % к итогу (f) |
| А | |
| Итого |
Решение:
По данным таблицы видно, что наибольшая частость (f =26) приходится на 36-й размер обуви.
Следовательно, мода (Мо) равна 36-му размеру, т.е. в данной совокупности именно этот размер обуви в ноябре 2010 года пользовался наибольшим спросом у женского населения.
4.3.6. По данным о содержании влаги в поступившей партии товара в магазин, определите моду:
| влажность, % (х) | число образцов (f) | накопленная частота S | середина интервала x
| x f
|
| А | ||||
| до 14 | ||||
| 14-16 | ||||
| 16-18 | ||||
| 18-20 | ||||
| 20 и более | ||||
| Итого | - | - |
Решение:
По данным таблицы, наибольшей влажностью обладают товары в интервале 14 - 16% (графа 1). Это и есть модальный интервал, величина интервала i = 2 (16 - 14), нижняя граница х = 14, частота fМо = 30, предмодальная частота fМо-1 = 20, а послемодальная частота f Мо+1 = 25.
Модальный процент влажности в партии товара составляет:
Мо = х0 + i = 14 + 2 
=15,3%
Таким образом, в данной совокупности поступившей партии товаров наибольший процент влажности приходится на 15,3%.
4.3.7. Определите медиану интервального ряда по данным о содержании влаги в поступившей партии товара в магазин:
| влажность, % (х) | число образцов (f) | накопленная частота S |
| А | ||
| до 14 | ||
| 14-16 | ||
| 16-18 | ||
| 18-20 | ||
| 20 и более | ||
| Итого | - |
Решение:
Для определения медианы в интервальном ряду сначала находим номер медианы:
N =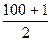 
= 50,5%
Накапливаем частоты (графа 2 таблицы) и определяем, что 50,5 образцов товара приходится на интервал (16 – 18).
Точное нахождение медианы на данном интервале определим по формуле:
= 16+2 
= 16%
Таким образом, половина (50%) партии товара имеет влажность менее 16%, и половина (50%) имеет содержание влаги в партии товара выше 16%.
