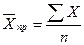Средняя величина в статистике представляет собой обобщенную количественную характеристику признака в совокупности в конкретных условиях места и времени.
Она показывает уровень признака, который относится ко всей совокупности. В зависимости от характера статистических данных применяют различные виды средних величин. В рядах распределения наиболее распространенными из них являются средняя арифметическая и средняя гармоническая простая и взвешенная.
|
|
|
Рис.3. Наиболее распространенные средние величины
в рядах распределения
4.1.1. Средняя арифметическая простая ранжированного ряда показателей соответствует простой совокупности объектов, в которой нет составных частей или групп, деленной на численность объектов исследования:
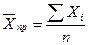, где
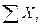- сумма показателей объектов исследования,
n - количество объектов исследования;
4.1.2. Средняя арифметическая взвешенная учитывает распространенность, повторяемость каждой варианты, т.е. удельный вес отдельных групп в общей совокупности и определяется по формуле:
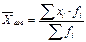, где:
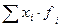- сумма произведений вариант (показателей) на их частоты,
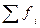- сумма численности (частот).
Для того, чтобы исчислить среднюю арифметическую интервального ряда, надо сначала определить среднюю для каждого интервала, а затем – среднюю для всего ряда.
Средняя для каждого интервала определяется по средней арифметической простой:
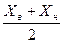
Для определения средней арифметической интервального ряда с открытыми интервалами необходимо, прежде всего, определить неизвестные границы интервалов первой и последней групп.
Если нижняя граница интервала отсутствует в первой группе, то его величина принимается равной интервалу последующей группы, а если верхняя граница отсутствует в последней группе, то его величина принимается равной интервалу предыдущей группы.
4.1.3. Средняя гармоническая величина представляет собой величину, обратную средней арифметической, исчисленную из обратных значений признака и применяется в том случае, когда в расчетах нет значений частот, а есть только варианты и произведение вариант и частот:
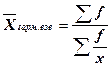, где:
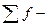сумма частот или повторяемости каждой варианты,
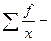сумма отношений частот к соответствующим вариантам.
Если частоты (веса) каждой варианты отсутствуют или равны между собой (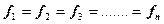
), то применяется средняя гармоническая простая:
.
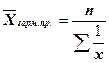4.1.4. Средняя геометрическая:
невзвешенная:
;
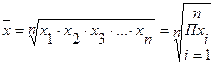взвешенная:
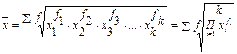, где:
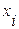- i-й вариант осредняемого признака;
n - объем совокупности;
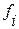- вес i-го варианта;
k - число вариантов осредняемого признака.
Пхi – произведение значений признака хi.
Основная область применения - осреднение индивидуальных показателей в динамике.
4.1.5. Средняя квадратическая:
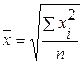- невзвешенная 
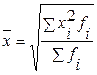- взвешенная
4.1.6. Средняя кубическая:
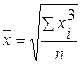- невзвешенная 
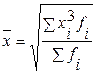- взвешенная,
где: 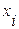- i -й вариант осредняемого признака;
n - объем совокупности;
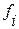- вес i -го варианта.
Основная область применения - расчет показателей вариации, взаимосвязи, структурных изменений, асимметрии.
4.1.7. Общий вид степенной средней величины:
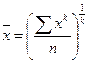, где:
k – показатель степени.
Данной степенной системой показателей могут быть представлены средние арифметическая, гармоническая, геометрическая, квадратическая и другие средние.
С изменением показателя степени «k» выражение данной функции меняется, и, в каждом отдельном случае, приходим к определенному виду средней:
при к =1 -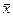 
= 
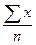- средняя арифметическая,
при к =-1 -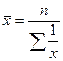 
- средняя гармоническая. 
при к = 0 -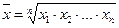 
- средняя геометрическая,
при к =2 -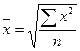 
- средняя квадратическая
и т.д. для любой степени.
Степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем больше показатель степени «К», тем больше и величина соответствующей средней:
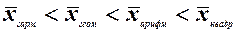
Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.
