Симметричное распределение (нормальное распределение)
Mo=Me
При симметричной форме распределении частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой: Аs = 0
Правосторонняя асимметрия
Mo Me 
Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии:
As > 0
Левосторонняя асимметрия
Me Mo
Отрицательная величина показателя асимметрии указывает на наличие левосторонней асимметрии:
As < 0
Решение типовых задач
5.7.1. По данным распределения возраста студентов одного из факультетов ВУЗа определимразмах распределения, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение.
| группы студентов по возрасту х, лет | число студентов fi | 
| 
| 
| 
| 
|
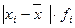
| A | ||||||
| 3,7 | 13,69 | 136,9 | ||||
| 2,7 | 7,29 | 510,3 | ||||
| 1,7 | 2,89 | 231,2 | ||||
| 0,7 | 0,49 | 49,0 | ||||
| 0,3 | 0,09 | 10,8 | ||||
| 1,3 | 1,69 | 270,4 | ||||
| 2,3 | 5,29 | 476,1 | ||||
| Итого | - | - | 1684,7 |
Решение:
Прежде всего находим самое маленькое значение возраста студентов
Xmin = 17 лет и самое большое Хmax = 23 года (графа А таблицы).
Находим разницу между максимальным и минимальным значением признака и получаем величину размаха, которая составляет:
R = 23 – 17 = 6 лет.
Для проведения дальнейших вычислений показателей вариации проведем дополнительные расчеты и запишем их в имеющуюся таблицу:
- определяем произведение значений признака(x 
) на соответствующие веса (fi) (графа 6). В итоге получаем сумму, равную 13060.
- рассчитаем среднюю величину по формуле средней арифметической взвешенной:
= 
= 
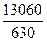= 20,7 года.
Для расчета среднего линейного отклонения находим абсолютное отклонение значений признака (x ) от средней величины (
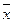) по модулю 
(графа 2).
Вычисляем произведения отклонений на их веса (fi) и подсчитываем сумму их произведений. Эта сумма равна 883 (графа 3).
Делим эту сумму (
) на сумму весов (fi), чтобы получить искомую величину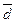 
:
= 
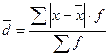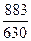= 1,4 года.
Таково в среднем отклонение вариантов признака от их средней величины.
Возведем в квадрат отклонения индивидуальных значений признака от их средней 
и запишем результат в графу 4 таблицы.
Затем квадрат отклонений умножим на веса (fi) и подсчитаем сумму, которая равна 1684,7 (графа 5).
Разделим эту сумму 
(x - ) 
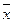f на сумму весов f , чтобы получить величину дисперсии:
= 
= 2,67
Извлечем корень квадратный из дисперсии и получим величину среднего квадратического отклонения:
= 
= 
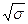= 1,63 года
Таким образом, каждое индивидуальное значение возраста студентов отклоняется от их средней величины на 1,63 года.
5.7.2. Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250.
Найдитесреднюю величину совокупности.
Решение:
Для нахождения средней величины воспользуемся методом отсчета от условного нуля или методом моментов:
= 
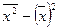, где
- средняя арифметическая из квадратов индивидуальных значений признака;
- квадрат среднего значения признака.
Тогда: = 
= 
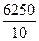= 625.
Средняя величина признака:
.
5.7.3. Для характеристики однородности совокупности следует вычислить показатели вариации: дисперсию, среднее квадратическое отклонение, коэффициент вариации (вычисления выполнить в таблице).
