2.4.1. Статистические таблицы оформляются врезультате сводки и группировки имеющихся данных проведенного наблюдения. Статистические таблицы обязательно содержат итоговые показатели и состоят из подлежащего и сказуемого.
Подлежащее таблицы показывает, о чем идет речь в таблице, оно расположено слева и представляет собой содержание строк.
Сказуемое таблицы расположено сверху и представляет собой содержание граф. Сказуемое показывает, какими признаками характеризуется подлежащее.
2.4.2. Построение статистических графиков является итоговым этапом сводки и группировки статистических данных. Графическое изображение – это самая эффективная форма представления статистических данных с точки зрения их восприятия.
Графиком называют условное, наглядное изображение статистических величин и их соотношений при помощи геометрических линий и фигур.
Каждый график должен включать следующие элементы: графический образ, поле графика, масштабные ориентиры и систему координат.
Графический образ – геометрические знаки, совокупность точек, линии, фигуры, с помощью которых изображаются статистические величины.
Поле графика представляет собой пространство, в котором размещаются геометрические знаки.
Масштабные ориентиры статистического графика определяются масштабом и масштабной шкалой.
Масштаб статистического графика – это мера перевода числовой величины в графическую,
Масштабная шкала – линия, определенные точки которой могут быть прочитаны как определенные числа. Шкала состоит из линии (носителя шкалы) и ряда намеченных на ней точек, расположенных в определенном порядке.
Масштабом равномерной шкалы называется длина отрезка, принятого за единицу и измеренного в каких-либо мерах.
Для размещения геометрических знаков в поле графика необходима система координат. Наиболее распространенной является система прямоугольных координат.
По способу построения графики делятся на линейные графики, диаграммы, картограммы, картодиаграммы.
К классу линейных графиков относятся: полигон, кумулята и кривая Лоренца.
Полигоном называют ломаную линию, отрезки которой соединяют точки Х i и fi,
где: Хi – значение признака
fi – частота.
Полигон применяют для дискретного ряда распределения.
Кумулята – ломаная, составленная по накопленным частотам или частостям, координатами точек которой являются Хi и fi,
где: Хi – значение признака, для интервального ряда – верхняя граница значений (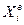 );
);
fi – накопленная частота.
Начальная точка ломаной интервального ряда распределения - нижняя граница значения ( ) в первой группе.
) в первой группе.
Кривой Лоренца или кривой концентрации называют кривую относительной концентрации суммарного значения признака. Она представляет собой ломаную, координатами точек которой на оси абсцисс являются накопленные относительные частоты, а на оси ординат – накопленное (нарастающим итогом) значение признака Хi.
Чем ближе кривая Лоренца к прямой линии, тем распределение признака более равномерное, т.е. концентрация меньше. Чем кривизна кривой больше, тем распределение более неравномерное, т.е. концентрация больше.
К классу диаграмм, прежде всего, относят гистограмму (столбиковую диаграмму), а также диаграммы полосовые, ленточные, круговые, линейные, квадратные, секторные, фигурные и др.
Гистограмма – это ступенчатая фигура, состоящая из прямоугольников, основания которых равны величине интервала в группе, а высоты, которых равны плотности в группе (абсолютной или относительной).
При построении столбиковых диаграмм данные изображаются в виде столбиков одинаковой ширины, но различной высоты, в зависимости от числовых значений изображаемых величин по определенному масштабу.
Разновидностью столбиковых диаграмм являются ленточные и полосовые диаграммы. Они изображают размеры признака в виде расположенных по горизонтали прямоугольников одинаковой ширины, но различной длины, пропорционально изображаемым величинам. Начало полос должно находиться на одной и той же вертикальной линии.
Секторные диаграммы удобно использовать для изображения структуры явления, в этом случае круг делится на секторы, пропорциональные долям частей явлений. Круг принимается за целое (100%) и разбивается на секторы, дуги которых пропорциональны значениям отдельных частей изображаемых величин. Дуга каждого сектора (или величина цетрального угла) определяется по формуле:

 , где:
, где: 
360◦ – площадь круга;
d – удельный вес изображаемого явления в процентах.
Если статистические данные представлены в абсолютных величинах, то формула для определения дуги приобретает вид:
 , где:
, где:
b – величина изображаемого явления в абсолютных величинах.
Для построения круговых и квадратных диаграмм надо провести предварительные расчеты, так как имеющиеся статистические данные (Di) соответствуют площадям геометрических фигур (кругов или квадратов).
Чтобы построить круг, необходимо найти радиус круга по формуле:
S =  R
R 
R  =
=  =
= 

Чтобы построить квадрат, необходимо найти сторону квадрата, исходя из формулы площади квадрата:
S = a 
a  =
=  =
= 
З нак Варзара применяют для наглядной характеристики трех взаимосвязанных величин - это прямоугольник, в котором основанием является один показатель, высотой - другой, а произведение основания на высоту характеризует величину производного третьего показателя.
Фигурные диаграммы строятся двумя способами: сравниваемые статистические величины (Di) изображаются фигурами – символами разных размеров пропорционально объемам этих совокупностей, либо разной численностью одинаковых знаков-символов, каждому из которых придается определенное числовое значение.
Для графического изображения пространственного распределения какого-либо статистического показателя применяют картограммы, которые бывают фоновые и точечные.
Картограмма – это сочетание диаграммы с географической картой.
На фоновых картограммах распределение изучаемого явления по территории изображается различными раскрасками территориальных единиц с разной густотой цвета или штриховкой различной интенсивности.
На точечной картограмме символами графического изображения статистических данных являются точки, размещенные в пределах определенных территориальных единиц. Каждой точке придается конкретное числовое значение.
Картограмма применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака в совокупности для выявления закономерности распределения этого признака.
Решение типовых задач
2.5.1. Имеются данные о товарообороте промышленных предприятий за отчетный период:
| № магазина | товарооборот, млн. руб. | |
| по договору | фактический | |
| 10,0 | 10,1 | |
| 12,0 | 12,2 | |
| 8,0 | 7,6 | |
| 50,0 | 52,0 | |
| 40,0 | 40,4 | |
| 12,0 | 12,6 | |
| 10,0 | 9,5 | |
| 30,0 | 32,6 | |
| 20,0 | 20,2 | |
| 25,0 | 25,6 | |
| 15,0 | 15,3 | |
| 20,0 | 20,6 | |
| 35,0 | 35,7 | |
| 12,0 | 11,0 | |
| 50,0 | 52,0 | |
| 40,0 | 40,8 | |
| 60,0 | 63,0 | |
| 30,0 | 30,9 | |
| 80,0 | 83,2 | |
| 70,0 | 72,1 | |
| Итого: | 647,4 |
1. Сгруппируйте предприятия по размеру фактического товарооборота, выделив следующие группы: предприятия с товарооборотом до 20 млн. рублей включительно; от 20 до 50 млн. рублей включительно; от 50 млн. рублей и выше и составьте простую перечневую групповую таблицу.
2. Определите в сказуемом таблицы товарооборот по договору, фактический и уровень выполнения товарооборота по договору по каждой группе.
Решение:
Составим и заполним разработочную таблицу, в которую запишем предприятия с товарооборотом до 20 млн.рублей включительно:
| № предприятия | товарооборот, млн.рублей | |
| по договору | фактический | |
| 10,0 12,0 8,0 12,0 10,0 15,0 12,0 | 10,1 12,2 7,6 12,6 9,5 15,3 11,0 | |
| итого | 79,0 | 78,3 |
Далее построим две аналогичные таблицы по предприятиям с товарооборотом от 20 до 50 млн. рублей и с товарооборотом от 50 млн. рублей и выше.
В полученных таблицах предприятия будут сгруппированы по заданному группировочному признаку «размеру фактического товарооборота».
Следующим этапом составим сводную группировку промышленных предприятий по размеру фактического товарооборота, определим итоговое сказуемое в каждом столбце таблицы и уровень выполнения товарооборота по договору по каждой группе, для чего добавим ещё одну дополнительную графу «абсолютное отклонение»:
| группы предприятий по размеру товарооборота, млн. руб. | количество промышленных предприятий | товарооборот, млн. руб. | абсолютное отклонение, млн. руб. | |
| по договору | фактический | |||
| А | ||||
| до 20 | 78,3 | - 0,7 | ||
| 20-50 | 246,8 | + 6,8 | ||
| 50 и выше | 322,3 | +12,3 | ||
| Итого: | 647,4 | + 18,4 |
Вывод:
В целом сумма превышения фактического товарооборота по 20 предприятиям составила 18,4 млн. руб. В первой группе предприятий с товарооборотом до 20 млн. рублей договорные обязательства не были выполнены, поэтому размер потерь составил 0,7 млн. рублей. Во второй группе предприятий с товарооборотом от 20 до 50 млн. руб. договорные обязательства были перевыполнены на 6,8 млн. руб. В третьей группе предприятий с товарооборотом от 50 млн. рублей и выше договорные обязательства перевыполнены на 12,3 млн. рублей.
2.5.2. Необходимо провести перегруппировку данных, образовав новые группы с интервалами до 500, 500-1000, 1000-2000, 2000-3000, свыше 3000 тыс. рублей по данным о распределении контрактов акционерного общества по величине прибыли:
Распределение контрактов акционерного общества «Звезда»
По величине прибыли
| № группы | группы контрактов по величине прибыли, тыс. руб. | число контрактов, единиц |
| до 400 | ||
| 400-1000 | ||
| 1000-1800 | ||
| 1800-3000 | ||
| 3000-4000 | ||
| 4000 и более | ||
| итого: |
Решение:
В первую новую группу войдет полностью 1-я группа контрактов и часть
2-й группы. Чтобы образовать группу до 500 тыс. руб., необходимо от интервала 2-й группы взять 100 тыс. руб., для чего определим величину интервала второй группы, которая составляет 600 тыс. рублей (1000-400). Следовательно, необходимо взять от нее 1/6 (100:600) часть и перенести ее в новый первый интервал. Аналогичную же часть (1/6) во вновь образуемую новую группу надо взять и от числа контрактов, т.е. от 20 (20 х 1/6 = 3 контракта). Тогда в новой группировке в 1-й группе будет 19 контрактов
(16 + 3).
Вторую новую группу по величине прибыли от 500 до 1000 тыс.рублей образуют оставшиеся контракты 2-й группы за вычетом отнесенных к 1-й, т.е. 20 – 3 = 17 ед.
Во вновь образованную третью группу войдут все контракты 3-й группы и часть контрактов 4-й группы. Для определения этой части контрактов от интервала 1800-3000 (величина интервала равна 3000-1800=1200 тыс. руб.) нужно добавить к предыдущему 200 тыс. руб. (чтобы верхняя граница интервала была равна 2000 тыс. руб.). Следовательно, необходимо взять часть интервала, равную 200:1200, т.е. также 1/6. В этой группе 74 контракта, значит, надо взять 12 единиц (74 х 1/ 6 = 12). В третью новую группу по величине прибыли от 1000 до 2000 тыс.рублей войдет: 44 + 12 = 56 контрактов.
Во вновь образованную четвертую группу войдет: 74 – 12 = 62 контракта, оставшихся от прежней 4-й группы.
Пятую, вновь образованную группу по величине прибыли свыше 3000 тыс. рублей, составят контракты 5-й и 6-й прежних групп: 37 + 9 = 46 контрактов.
Вторичная группировка распределения контрактов акционерного общества «Звезда» по величине прибыли показана в таблице:
| № группы | группы контрактов по величине прибыли, тыс. руб. | число контрактов, единиц |
| до 500 | ||
| 500-1000 | ||
| 1000-2000 | ||
| 2000-3000 | ||
| 3000 и более | ||
| Итого: |
2.5.3. Приизучении покупательного спроса в универсальном торговом доме в течение дня зарегистрирована продажа следующих размеров женских брючных костюмов:
46 52 52 48 48
48 48 46 52 52
44 50 48 48 50
46 54 54 52 48
50 50 50 50 46
46 48 48 52 48
46 52 44 48 48
50 50 48 54 50
46 50 50 48 48
54 48 48 48 48
Постройте ряд распределения и полученные результаты сравните с типовой шкалой пошива брючных костюмов фабрикой, поставляющей их в торговый дом.
Типовая шкала пошива женских брючных костюмов:
| Размер | Всего | ||||||
| Число изделий, % к итогу |
Данные ряда распределения реализованного спроса и типовой шкалы пошива платьев изобразите в виде полигона распределения. Укажите модальную величину ряда распределения. Сделайте выводы о соответствии спроса и предложения.
Решение:
Данные наблюдения реализованного спроса, т.е. исходную информацию об изучении покупательного спроса, запишем в порядке возрастания от наименьшего значения к наибольшему, в результате получим ранжированный ряд распределения, на основании которого легче построить прерывный дискретный ряд распределения.
Запишем в таблицу результаты построения прерывного ряда распределения, где в качестве вариант X будут выступать размеры женских брючных костюмов, а в качестве частот f - количество костюмов (частоты, пересчитанные в проценты к итогу, называются частостями).
Всего была зарегистрирована продажа 50 различных размеров женских брючных костюмов.
По условию задачи определим, сколько раз спрашивается 44-й размер –
2 раза, 46-й - 7 раз, 48-й - 19 раз и т.д. Затем частоты (f – количество раз или количество костюмов) – пересчитаем в проценты к итогу.
Затем результаты покупательного спроса необходимо сопоставить с данными типовой шкалы пошива женских брючных костюмов. Так как типовая шкала дается в процентах к итогу (значения частот f 2), то реализованный спрос пересчитываем в процентах к итогу (значения частот f 1 ).






