Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается относительный показатель асимметрии (А s).
Существует несколько видов расчетов коэффициента асимметрии, например по формуле:
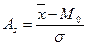, где:
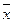- средняя величина ряда распределения,
М0 - центральный момент распределения,
σ - среднее квадратическое отклонение.
Величина показателя асимметрии (Аs)может быть положительной иотрицательной.
Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии (более длинная ветвь вправо).
Отрицательный знак показателя асимметрии говорит о наличии левосторонней асимметрии (более длинная ветвь влево).
Величина асимметрии может изменяться от -1 до +1 (для одновершинных распределений).
Чем больше абсолютная величина коэффициента асимметрии, тем больше степень скошенности вправо или влево.
Принято считать, что если коэффициент асимметрии Аs меньше 0,25. то асимметрия незначительная, а если Аs свыше 0,5, то асимметрия значительная.
При симметричном распределении Аs = 0, т.к. варианты равноудалены
от 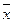и имеют одинаковую частоту.
Заостренность или крутизна графика распределения вычисляется с использованием центрального момента четвертого порядка по формуле:
, где:
M4 – центральный момент четвертого порядка,
среднее квадратическое отклонение в четвертой степени.
При измерении асимметрии эталоном служит симметричное распределение, для которого А3 = 0.
Для нормального распределения показатель асимметрии четвертого порядка равен 3 (А 4 = 3).
Для сравнения островершинности распределений в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и рассчитывается показатель эксцесса по формуле:
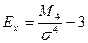
Эксцесс также может быть положительным и отрицательным.
У высоковершинных (островершинных) распределений показатель эксцесса (Ех) имеет положительный знак (+), а у низковершинных (плосковершинных) – отрицательный знак (-).
Предельным значением отрицательного эксцесса является значение
Ех = - 2, величина положительного эксцесса является величиной бесконечной.
Так как в нормальном распределении 
, следовательно, для нормального распределения показатель эксцесса равен нулю (Ех = 0).
Средняя квадратическая ошибка эксцесса исчисляется по формуле:
, где:
n - число наблюдений.
Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное распределение к типу нормального распределения.
Распределения, близкие к нормальному распределению, встречаются при изучении самых различных явлений развития природы и общества.
