Измеренным (отслеженным) па-
раметром является оценка X (г) — информационный параметр опорного
радиосигнала у \t, X (г)], вырабатываемого в процессе слежения с помощью генератора, управляемого напряжением (ГУН), управляемого (по параметру X) управляющим напряжением иу (г). Последний формируется с помощью дискриминатора (Д) и сглаживающей цепи (СЦ).
Дискриминатор вырабатывает напряжение г (е, t) = Ft {х (t, X),
у (/, X)} = LH4 (е), соответствующее нечетной функции от сигнала ошибки:

(17.59)
Выходом следящей схемы рис. 17.17 может служить либо опорный радиосигнал у (/, X), либо изме-
репный параметр X (t).
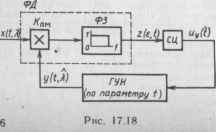
Примером следящего РПУ рис. 17.17 служит схема фазовой автопостройки (ФАП) рис. 17.18, в которой в качестве дискриминатора применяется простейший фазовый детектор (коррелятор), состоящий из перемножителя (коэффициент перемножения Ком) и формирующего звена (ФЗ), пропускающего без искажений с единичным усилением полосу биений сигнального х (t, X) и опорного у (t,X) напряжений.
Другим примером следящего РТУ рис. 17.17 может служить оптимальный демодулятор рис. 11.18 с оптимальным дискриминатором (ОД) в виде схемы рис. 11.14, работающей от двух опорных сигналов:

(17.60)
В рамках метода фильтрации информационного параметра схему рис. 17.17 стремятся свести к модели в виде петли автоматического регулирования (рис. 17.19) с входным воздействием X (t). Модель дискриминатора
г,„ (е,0 = F, {г = V— X} на-
 зывается статистическим эквивалентом на основе метода фильтрации информационного параметра.
зывается статистическим эквивалентом на основе метода фильтрации информационного параметра.
Обобщенные статистические эквиваленты дискриминаторов. Достаточно общую теорию построения статистических эквивалентов дискриминаторов разработали И. А. Большаков и В. Г. Репин [121. Суть ее сводится к следующему.
Запишем выходное напряжение произвольного дискриминатора в схеме рис. 17. 17 в общем виде z (е,г) =
=* F, {х (/, к), у (г, к)} = тг (г, 0 + 1(0.'где/и. (е, 0=<г(еД)>— математическое ожидание случайного процесса z (е, 0. a l(t) = = z°(e, 0 — его флуктуация. Если найдена (путем статистического анализа) корреляционная функция R. X X (т, е, 0 = < 2° (е, 02° (е, t + + т) >, то можно определить нестационарную спектральную плотность этого процесса:

В частном случае, когда про z (е,0 — стационарный, имеем

Это соответствует статистическ эквиваленту рис. 17.20, б. Здесь четная функция а (е) = тг (е) и; вается дискриминационной харш ристикой (ДХ), а четная функ b (е) = Y ~N (е) — флуктуацион характеристикой (ФХ). Ли1 ный участок ДХ в области |е|-
•s da(e) / имеет крутизну Ка = ^- \
При этом параметр е считают постоянным. Тогда процесс £ (0 аппроксимируют белым шумом со статистическими характеристиками R2 (т,е, 0 = N(e, 0 б (т), N(e,t) = = Nz (0, е, 0- Сделанное допущение позволяет переписать напряжение z (г, 0 в виде

(17.61)
где 1\ (0 — белый шум с единичной спектральной плотностью.
Алгоритму (17.61) соответствует статистический эквивалент (рис. 17.20, а), от которого требуется статистическая адекватность процессов z (е, 0 й гэк (е, 0- Чаще всего ограничиваются равенством математических ожиданий и корреляционных функций.
В линейном режиме слежения (|е| С 1) математическую модель СЭ (рис. 17.20, б) линеаризуют:

Если теперь белый шум £ (спектральная плотность Л/| = Л/0 + Л/2е2) разбить на сумму двух независимых шумов |j (спектральная плотность A/ji = N0) и 12 (спектральная плотность Nit = Л^е2), то гэк (е,0 можно представить в виде линейного статистического эквивалента рис. 17.20, в с алгоритмом

Здесь Чэк (г) — мультипликативный (параметрический) белый шум со спектральной плотностью Л\,эК = = N2IК\, а |эк — аддитивный белый шум со спектральной плотностью NUk - NJKI
Примеры нахождения статистических эквивалентов дискриминаторов в присутствии неинформативных шумовых помех. Рассмотрим примеры нахождения СЭ дискриминаторов, когда во входной смеси ыг = ис + + иш присутствует лишь шумовая помеха иш (t), не имеющая информативного параметра.
Примеры 17.7. Статистический эквивалент фазового дискриминатора рис. 17.18. Определим входную смесь

где Фс (/, X) — шс / — X, Фш (t) = ш01 — — 0 — полные фазы, а X = фс (/) — фазо-.вый информационный параметр.
Опорное напряжение от ГУН постулируем в виде

Введем коэффициент усиления К (/) = = 0,5/(пм-£г (t) и расстройки несущих частот сигнала, шума и генератора: Дсос — ■
— шс — ш„. А<ог = сог — 1лщ< Дш = <ог -
— Фс- Тогда получим решение для искомого статистического эквивалента:

(17.64)
Здесь введен сигнал ошибки (разность полных фаз сигнального и опорного напряжений на входах дискриминатора):

(17.65)
где Хс (t) = фс (/), Хг (/) - k (t) - Д«о< + + фго (/) - л/2.
Флу ктуационная шумовая составляющая" £ (г) = R (t) sin [6 (0 + ф (01 = = В (t) cos ф (/)-+- A (t) sin ф (t) зависит от компонент А (/), В (/) входного шума и фазы ф (0 = Д<ог / — МО + (я /2) —
- Ч>го (0-
Алгоритмам (17.64), (17.65) соответствует статистический эквивалент рис. 17.21,а. Как показывает статистический анализ, при широкополосном входном шуме (спектральная плотность Gm (/)) процесс £ (0 в СЭ (17.64) можно аппроксимировать белым шумом со спектральной плотностью Gt (/) = 2GU, (/г), где fx — частота ГУН, изменяющаяся в процессе слежения.
На рис. 17.21,6 представлен другой вариант СЭ [5], который получается из предыдущего, если шум £ (/) переписать в виде I (0 = I (е, /) = ls (0 sin t (t) +
+ |e (0 cos e (0, где g, (t) = В (t) * J X
С
x [Xc (0 -До >с/1 ± A (0 ^ IXC (0 -ДМ-
Статистический анализ показывает, что белые шумы £в, £с статистически независимы и имеют одинаковую спектральную плотность 2Gm (/с). Так как частота /с = = const, эта спектральная плотность в процессе слежения не меняется и может быть вычислена заранее. Статистический эквивалент рис. 17.21,6 линеаризуется (|е| < <С 1) и сводится к схеме рис. 17.20, в, где Кщ = К (f)Ec (0, чэк = Ь/Ес =
УЕС.
Пример 17.8. Статистический эквивалент оптимального дискриминатора в оптимальном демодуляторе. Найдем СЭ оптимального дискриминатора рис. 11.14, когда на его входе действует смесь произвольно-модулированного сигнала и белого нестационарного гауссова шума: х (t, X) = ис (I, иш (0 = Re X
X £Q (/, X) е/0>с j - п (0 со спектраль-
ной плотностью N„ (/). Запишем опорные сигналы через комплексные огибающие:

Тогда для низкочастотного выходного эффекта ОД г (г, t) = |2/V0 (г)]-1 у2 (t Д) X
X \х (/, А.) — у, (/, X)] в полосе ФЗ можно получить решение г (е, /) = гс (е, г) -f Н £ (/). где гс (е, 0 = К U) Re {(<Э£С(/.
к )1д ~к) |£* (/, X) — £с (/, Здесь» —
индекс комплексного сопряжения и введены сигнал ошибки (17.59) и коэффици-ет передачи К (О \2N0 (0l_1- Эквивалентный белый шум в СЭ J (г) имеет спектральную плотность /Vg (/) = К (01
|<Э£0 (/, Х)/дк\*.
Дальнейшая конкретизация решений зависит от вида модуляции. Так, при амплитудной модуляции, когда £с (/, X) =. = £с0 (I + >.) е-/*с0; дЕс (/, Т)/<ЭХ = £со е /1*'с», имеем линейный СЭ вида рис. 18.20, в: г (г, 1) - /Сд (/) [е (/) +
С (01. где /Сд (0 = £c2o/2/V0 (0 = — P cnfNa (/), £.= |//Сд — белый шум со спектральной плотностью (t) = /Сд 1 (/).
В случае фазовой модуляции имеем СЭ в виде z (f, 0 = /Сд (/) [sin е (/) -[ £ (/)].
§ 17.7. Математическое моделирование РПУ методом информационного параметра
Основные особенности метода информационного параметра. Сущность метода информационного параметра, применяемого, как правило, для моделирования следящих радиоустройств типа рис. 17.17, заключается в замене такого устройства петлей автоматического регулирования типа рис. 17.19 с низкочастотным входом в виде отслеживаемого информационного параметра X (t).
Для решения подобной задачи необходимо выполнить следующие операции:
заменить входную смесь х (t, X) информационным параметром X (г);
заменить дискриминатор его статистическим эквивалентом, как описано в § 17.6;
заменить ГУН его низкочастотной моделью;
сглаживающую цепь оставить неизменной.
После получения модели типа рис. 17.19 ее дальнейшее моделирование осуществляется различными способами:
1) с помощью математического описания схемы системой интеграль-
i ных (интегродифференциальных) урав-1 нений;
2) с помощью математического
• описания схемы нелинейным диффе-I ренциальным уравнением высокого. порядка;
3) с помощью других способов,: применяемых в теории автомат ическо-: го регулирования, например путем i предварительного упрощения схемы i методом статистической линеаризации.
Степень адекватности реальной
• схемы рис. 17.17 и ее модели I (рис. 17.19) проверяют по идентично-
• сти дифференциальных (интегродиф-» ференциальных) уравнений для сиг-i нала ошибки е (/).
Математические модели ГУН. В | реальных следящих РТУ, обеспечива-i ющнх в РПУ синхронизацию (ФАП,
ЧАП), в качестве ГУН в схеме рис. 17.18 обычно применяют генератор с самовозбуждением, частота которого (под воздействием управляемой емкости с(иу)) управляется напряжением иу (t).
В простейшей модели ГУН регулировочная характеристика — линейная:
ft>r(0 = «rK) = wrU— suy. (17.66)
Тогда можно получить математическую модель ГУН [51, показанную на рис. 17.22. Здесь выходной величиной модели является (как этого требует СЭ фазового дискриминатора рис. 17.21, а, б) фаза:

w = suy=X', Aco0 = col0 — сос. (17.67)
В простейшей модели ГУН амплитуда считается постоянной: £,.(/) — = const, а начальной фазой ipre (t) (в отсутствие управляющего напряжения) можно пренебречь.
В усложненной модели ГУН учитывают амплитудные £г (t) и фазовые фго (j) флуктуации за счет собственных шумов генератора и шумов, заложенных в управляющее напряжение 15].
Примеры математического моделирования методом информационного параметра. Рассмотрим три примера.
Пример 17.9. Математическая модель ФАП в присутствии неинформативных шумовых помех. Возьмем схему ФАП рис. 17.18 со статистическим эквивалентом ФД рис. 17.21, б. В качестве модели ГУН используем упрощенную модель
рис. 17.22. Тогда придем к математической модели ФАП, показанной на рис. 17.23. Здесь введены: Л"ФЛ11 = 0,5/Спм/Сф S — коэффициент передачи ФАП; S — крутизна регулирования в ГУН; /Сф — коэффициент передачи СЦ ни постоянном токе; h\ U, т) = *ф xh (г, т) — нормированная импульсная характеристика СЦ. Здесь же показаны модели дополнительных каналов ГУН |5]: амплитудного (формирует напряжение Ег (/)) и фазового (формирует фазу фг0 (0 — л/2).
Полученная модель является достаточно строгой и учитывает нестационарные влияния сигнала ошибки е (/) на статистические характеристики эквивалентных шумов в петле слежения. Существующие модели обычно приводятся без учета этого важного влияния.
В математической модели ФАП рис. 17.23 имеется три выхода: «фазовый»
выход (А): кг (0 = Т(/) + [фго U) —
— л/2 — Аю0/|; «частотный» выход (Б):
w (t) = Suy V) — d к (Л/d/, выход «по ошибке слежения» (В): 8 (/) = X (0 —
— Г(/) — Kv. V) - л/2 — До)0/|.
Составим систему интегродифференци-альных уравнений, описывающих математическую модель ФАП рис. 17.23. Используя временной метод анализа, находим


В качестве исходных данных моделирования приходится использовать: амплитудную модуляцию радиосигнала £с(/): начальную расстройку Дм,— сого— шс; коэффициент передачи петли ФАП КФАП; статистические параметры эквивалентных шумов |, (г), 1С (О (спектральную плотность °-£s= °V = 2Сш (/с)); параметры модели ГУН:, импульсную характеристику сглаживающей цепи hN (t. т)
Иногда при моделировании переходят от системы (17.68) к дифференциальныи уравнениям.
Пусть сглаживающая цепь с места ционарной импульсной характеристикой hN (t, т) описывается дифференциальныи линейным уравнением с переменными коэф фициентами

(17.09
По определению импульсной харакге ристики, если на вход сглаживающей цст подать сигнал в виде 6-функции Дирак v (t) = b(t — т), то выходной реакцией бу дет w (I)— hK (i, t — т), так что
 (17.70
(17.70
где производные взяты по времени t.
Используем первое из уравнени] (17.68) и составим высшие производные сиг нала ошибки к С), считая для общност Дсо0= Д(о„ (/) функцией времени (ест
Где

Используя свойство 6-функции Дирака  юлучаем
юлучаем

Подставляя (17.74) в (17.73), находим

Используя формулы (17.68), получаем окончательное дифференциальное уравнение 1етли ФАП рис. 17.23:

Здесь «внешними возмущениями» следует считать величины Аш„ (/)', А (/), £го(').!.,(/), >f(0. амплитуду сигнала Ее (О и гетеродина Ег (I). Под эти возму-Цения и отрабатывается сигнал слежения ■(')•
Ш
ишшшшшшшшшшшшшшлшшшттшшшшлшшшшшшшшшшшвшшлшшЪЪЪЪЪЪЪЪЪЪш
■
Если, например, сглаживающий цепь— безынерционное звено с усилением Кф, то в (17.76) следует положить a0~b0=. 1, о; = 0, i I, 6ц = 0, I. Это дает дифференциальное уравнение первого порядка

Сделав допущения о постоянстве ампли-туд Er(t)=-F.r--Ur. Ec(t) = Ee=Uc. Дсо0 (/) - Д(оп = Д„. iro (<) = г|го = const, сменив обозначения е = n/2 + <p,d/d/ = р. A(r)=f (/), £,= аш. jc = *m. получим
РфСН -КфАП^сЮ +вш/(/с) СОБф —
— (fem/t/c)sin9|- До -i pi|-(/).
Полученное дифференциальное уравнение совпадает с (10.13) при допущениях
Н (Р) = Кф- Л'фдп — 5у *фдАф, что свидетельствует о полном соответствии модели ФАП рис. 17.23 оригиналу.
Пример 17.10. Математическая модель ФАП в присутствии информативных помех. Пусть на вход фазового дискриминатора рис. 17.18 подана аддитивная смесь радиосигнала uc(t, Ас) = Ес (t) cos \u>ct — **.(/)], имитационной помехи ип (/, Ап) и гауссова у.ткополосного шумапш(<).
Формирование имитационной помехи из полезного радиосигнала представим в виде эквивалентной модели по комплексной огибающей, согласно которой комплексная огибающая помехи E„(t) формируется из комплексной огибаюшей сигнала Ес (/) = Ес (/) х Хехр |—/Яс (/)] путем ее задержки на времо т„ и умножения на помеховую функцию
£ц(0 — n + S (0JwPf~/Ч(01 с Дополнительным усилением k„ [5]. Это позволяет записать


При этом подразумевается, что входная и выходная несущие частоты модели имитационной помехи одинаковы и равны wc.
Как и в примере 17.7, запишем полное напряжение смеси на входе фазового дискриминатора:
ращенной форме обозначены амплитуды Fo-= £г(7). /•„=-£„(/) - fe„£c(/-T„)[l + !?(/)]. R:-R(f).
Опорное напряжение {/(/, Х) в схеме рис. 17.18 постулируем, как в примере 17.7. Тогда выходное напряжение фазового дискриминатора можно представить в виде
z(t) -г (ев, е„. t)^K(t) [гс(ес, /) + + гп(Еп, 0+£«(')]■ (17-77>
Здесь Л' (0 = 0,5 (|ш£Г(1)н введены сигнальная и помеховая составляющие:
гс(ег., 0 <=£«:(0 sin ес (/■), (17 78)
2П («п. ') (0 sin е„ (/),
а также шумовое напряжение
|В«(г) = Л (0 sin [л/2-;-Ф г(0 -Фш (01.
(17.79)
где Фг(/) <,),./--ф,.„(п - Г (0-
Под сигналами ошибок подразумеваем

(17.80)
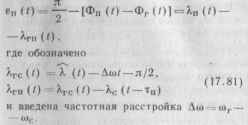
Полученные решения приводят к статистическому эквиваленту фазового дискриминатора рис. 17. 18 в присутствии информативных помех, отличающемуся от эквивалента рис. 17.21, а типичной двухцеле-вой ситуацией, когда на входе имеются два информативных параметра Хс(/), kn(t).
Соединив полученный статистический эквивалент с моделью ГУН (см. пример 17.9), можно получить полную модель ФАП в присутствии информативной и шумовой помех и описать ее с помощью либо инте-гродифференциальных уравнений, либо дифференциального уравнения высокого порядка.
Пример 17.11. Математическая модель оптимального демодулятора. Пусть на вход оптимального демодулятора рис. 11.18 подается смесь фазомодулированного сигнала ис ('• к) — Есо cos (<ос/ — X) и белого гауссова шума п (v) со спектральной плотностью Ый (/). Тогда, используя СЭ оптимального дискриминатора из формулы (17.8). сведем схему рис. 11.8 к математической модели рис. 17.24, являющейся частным случаем модели рис. 17.19.
ЗАКЛЮЧЕНИЕ
В данном учебном пособии курс «Радиоприемные устройства» излагался по схеме «от частного к общему» в соответствии с программой.
Вначале рассматривались общие структуры приемников, а также воздействующие на них сигналы и помехи. При этом было показано, что входные сигналы приемника, прошедшие тот или иной радиоканал, как правило, становятся случайными процессами с флуктуирующими амплитудой и фазой.
Далее достаточно детально исследовались отдельные узлы и блоки, из которых состоят современные приемники: входные цепи, усилители радиочастоты, в том числе малошумя-щие усилители СВЧ, преобразователи частоты и усилители промежуточной частоты, детекторы, автоматические регулировки усиления, частоты, фазы. Отдельные типовые узлы и блоки приемников рассмотрены в основном на базе интегральных микросхем, сложные (крупноблочные) функционально законченные изделия с заданными параметрами — на основе интегральных приемных СВЧ-модулей.
Учитывая разнообразие помехо-вой обстановки, в которой работают приемники, была обоснована главная их задача — наилучшее восстановление полезной информации при воздействии помех. В этой связи излагались основы статистической теории радиоприема. Отметим, что при изложении материала использован единый статистический подход к решению задач обнаружения сигнала и оценки его параметров применительно к радиолокационным, радионавигационным, ра-.
диотелеметрическим, радиосвязным и другим приемникам радиосистем извлечения и передачи информации. Для синтеза приемников измерения случайных процессов излагались основы оптимальной нелинейной фильтрации.
Единая методология синтеза оптимальных структур приемников разных радиосистем извлечения и передачи информации позволила далее исследовать типовые структуры приемников не по их назначению и принадлежности к той или иной радиосистеме, а по типам сигналов при заданных видах модуляции. Выбрано четыре основных вида сигнала, которые в той или иной мере используются в радиосистемах извлечения и передачи информации: импульсные (простые и сложные), импульсные аналоговые (КИМ, АИМ и др.), дискретные (АМн, ЧМн, ФМн), непрерывные (AM, ЧМ, ФМ). Такой широкий набор сигналов позволил охватить большинство современных приемников как специального назначения, так и общего пользования.
Для любого типа сигнала была предпринята попытка единого подхода к рассмотрению функциональных структур соответствующих приемников. Вначале, на основе теории оптимального приема, рассматривалась оптимальная структура приемника, которая обычно сводится к когерентному или квазикогерентному приему. Затем приводились структуры приемников, полученных из инженерного синтеза. Далее производилось сравнение помехоустойчивости оптимального и неоптимального приемников
при различных соотношениях сигналу помеха на их входе. Отмечались особенности структур и выходных характеристик приемников.
В связи с освоением все более коротких волн рассматривались приемные устройства оптических сигналов, особенности их структуры, специфические вопросы приема сигналов.
В конце учебного пособия представлен материал по математическому моделированию радиоприемного устройства.
Естественно, что ограниченный объем книги не позволил глубже рассмотреть ряд вопросов, а некоторые проблемы вообще не затрагивались. Так, вопросы помехоустойчивости, а также соответствующая теория и техника оптимального приема даны в основном для аддитивной помехи в виде белого нормального шума. Воз-
действие более сложных помех и ш мов рассматривается обычно в сг циальных дисциплинах.
Успехи в области микроэлектр ники непрерывно повышают урове интеграции изделий, сводя узлы блоки приемников в большие инт тральные схемы (БИС). Эта совреме ная элементная база наряду с цифр вой обработкой сигнала (цифров] синтезаторы частот, АРУ, ФАПЧ, л модуляторы и другие узлы) образу новое поколение приемников, обл дающих высокой надежностью, м лыми массой и габаритами, высою помехоустойчивостью.
После освоения этого основно курса рекомендуется самостоятелы изучать литературу по различным в просам теории, техники и проектир вания приемников различного назн чения.
СПИСОК ЛИТЕРАТУРЫ
1. Аналоговые и цифровые интегральные схемы /Под ред. С. В. Якубовского. —
М.: Советское радио, 1979.






