Приклад 1. Коливальний контур має індуктивність 1,6 мГн, електричну ємність 0,04 мкФ і максимальну напругу Umax на клемах рівну 200 В. Визначити максимальну силу струму в контурі. Опором контуру знехтувати.
Дано:
L = 1,6 мГн
C = 0,04 мкФ
Umax = 200 В
____________
Іmax –?
Розв’язування. Згідно з законом збереження енергії, максимальна енергія електричного поля конденсатора дорівнює максимальній енергії магнітного поля котушки індуктивності. Тому
 .
.
Звідки
Imax = Umax  .
.
Підставимо числові значення
Imax = 200 ×  = 1 A.
= 1 A.
Відповідь: Іmax = 1 А.
Приклад 2. Індуктивність коливального контуру дорівнює 0,5 мГн. Контур резонує на довжину хвилі 300 м. Визначити електроємність такого контуру. Опором контуру знехтувати.
Дано:
L = 0,5 мГн
l = 300 м
__________
С –?
Розв’язування. Виразимо довжину електромагнітної хвилі через швидкість поширення і період коливань контуру
l = с Т,
де с = 3 × 108 м/с – швидкість електромагнітних хвиль у вакуумі.
Період коливань контуру дорівнює
Т = 2p  .
.
Тому
l = 2p с  .
.
Звідки знаходимо ємність конденсатора
С =  .
.
Підставимо числові значення
С =  = 5,1 × 10-11 Ф.
= 5,1 × 10-11 Ф.
Відповідь: С = 51 пФ.
Приклад 3. В середовищі, для якого e = 4,00 і m = 1,00, поширюється плоска електромагнітна хвиля. Амплітуда електричного вектора хвилі Еmax = 200 В/м. На шляху хвилі розміщена поглинаюча поверхня, яка має форму диска радіусом r = 300 мм. Яку енергію поглинає ця поверхня за t = 1,00 хв? Період хвилі Т << t.
Дано:
e = 4,00; m = 1,00
Еmax = 200 В/м
r = 300 мм
t = 1,00 хв
_______________
W –?
Розв’язування. Енергія, яка переноситься електромагнітною хвилею за одиницю часу через одиницю поверхні, перпендикулярно до напрямку поширення хвилі, визначається вектором Пойнтінга
 , (1)
, (1)
де  – вектор густини потоку енергії.
– вектор густини потоку енергії.
В електромагнітній хвилі вектори  і
і 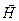 взаємно перпендикулярні, тому модуль вектора Пойнтінга дорівнює
взаємно перпендикулярні, тому модуль вектора Пойнтінга дорівнює
 . (2)
. (2)
Оскільки обидві величини Е і Н, які характеризують електромагнітну хвилю, в кожній її точці змінюються в часі за законом синуса або косинуса і знаходяться в однакових фазах, співвідношення (2) можна записати так:
R = E0 sin wt H0 sin wt = E0 H0 sin2 wt. (3)
Таким чином, величина R є функцією часу, а формули (2) і (3) дають лише миттєві значення цієї величини.
Нехай через площадку S в напрямі перпендикулярному до напряму поширення хвилі переноситься за час t енергія W. Тоді густина потоку
R =  (4)
(4)
Через площадку S буде перенесена за час t енергія W, яка міститься в об’ємі циліндра з основою S і висотою υt, тобто
W = R S t. (5)
З урахуванням (3) маємо
W = E0 H0 S t sin2 wt. (6)
Згідно з теорією електромагнітних хвиль, густини енергії електричного і магнітного полів хвилі в будь-який момент часу однакові як для Е і Н, так і для Е0 і Н0. Тому
 . (7)
. (7)
З формули (7) знаходимо Н0 і підставляємо в (6)
W =  S t sin2 wt. (8)
S t sin2 wt. (8)
Оскільки за умовою задачі Т << t, то величину sin2wt можна усереднити в часі, тобто
 .
.
Остаточно одержуємо
W =  .
.
Підставимо числові значення
W =  × 4 × 104 × 9 × 10-2 × 3,14 × 60 = 1800 Дж.
× 4 × 104 × 9 × 10-2 × 3,14 × 60 = 1800 Дж.
Відповідь: 1800 Дж.
Задачі
303. Точка виконує гармонічні коливання. Найбільше зміщення хmax дорівнює 10 см, найбільша швидкість υмах = 20 см/с. Знайти циклічну частоту ω коливань і максимальне прискорення amax.
Відповідь: 2 с-1; 40 см/с2.
304. Точка виконує коливання за законом х = Asinωt. У деякий момент часу зміщення х1 точки виявилося рівним 5 см. Коли фаза коливань збільшилася вдвічі, зміщення х2 стало дорівнювати 8см. Знайти амплітуду А коливань.
Відповідь:  .
.
305. Рівняння коливань точки має вигляд х = A cosω (t+ τ), де ω= πс -1; τ = 0,2 с. Визначити період Т і початкову фазу φ коливань.
Відповідь: 2 с; 36о.
306. Точка виконує коливання за законом х = А cos (ωt+ φ), де А = 4 см. Визначити початкову фазу φ, якщо: а)  і
і  б)
б)  см і
см і  в) х(0) =
в) х(0) =  см і
см і  г) х(0)=
г) х(0)=  см і
см і  . Побудувати векторну діаграму для моменту часу t = 0.
. Побудувати векторну діаграму для моменту часу t = 0.
Відповідь:;  ;
; 
 ;
;  .
.
307. Точка виконує коливання з амплітудою A = 4 см і періодом Т = 2 с. Написати рівняння цих коливань, вважаючи, що в момент часу t = 0 зміщення х(0) = 0 і υ(0)< 0. Визначити фазу (ωt + φ) для двох моментів часу: а) коли зміщення х = 1 см і υ > 0; б) коли швидкість υ = – 6 см/с і х < 0.
Відповідь:  , де А = 4см,
, де А = 4см,  рад/с,
рад/с,  ;
;
 ;
;  .
.
308. Точка виконує коливання за законом х = A cosωt, де А = 5 см;  = 2 с-1. Визначити прискорення а точки в момент часу, коли її швидкість υ = 8 см/с.
= 2 с-1. Визначити прискорення а точки в момент часу, коли її швидкість υ = 8 см/с.
Відповідь:  .
.
309. Максимальна швидкість υmах точки, що виконує гармонічні коливання, дорівнює 10 см/с, максимальне прискорення amах = 100 см/с2. Знайти циклічну частоту ω коливань, їх період Т і амплітуду А. Написати рівняння коливань, прийнявши, що початкова фаза дорівнює нулю.
Відповідь:  ; 0,628 с; 1 см;
; 0,628 с; 1 см;  .
.
310. Коливання точки відбуваються за законом х = A cos (ωt + φ). У деякий момент часу зміщення х точки дорівнює 5 см, її швидкість υ = 20 см/с і прискорення a = – 80 см/с2. Знайти амплітуду А, циклічну частоту ω, період T коливань і фазу (ωt + φ) у розглянутий момент часу.
Відповідь:  ;
;  ;
;  ;
;  рад.
рад.
311. Точка бере участь у двох однаково направлених коливаннях х1 = А1 sin ωt і х2 = А2 cos ωt, де А1 = 1 см; А2 = 2 см; ω =1с-1. Визначити амплітуду А результуючого коливання, його частоту v і початкову фазу φ. Знайти рівняння цього руху.
Відповідь: А = 2,24 см;  ;
;  рад;
рад;  , де
, де  .
.
312. Матеріальна точка виконує гармонічні коливання уздовж осі х за законом:  , де t – час у секундах, х – у сантиметрах. Визначити амплітуду зміщення А и період коливань Т. Знайти зміщення х, швидкість
, де t – час у секундах, х – у сантиметрах. Визначити амплітуду зміщення А и період коливань Т. Знайти зміщення х, швидкість  і прискорення а матеріальна точки в момент часу t = 4,0 с.
і прискорення а матеріальна точки в момент часу t = 4,0 с.
Відповідь: А = 6,0 см; Т = 2 с; х = 4,85 см; υ = 11,07 см/с;
а = 47,6 см/с2.
313. Частинка виконує прямолінійні гармонічні коливання. Амплітуда швидкості частинки  = 22 см/с, амплітуда її прискорення
= 22 см/с, амплітуда її прискорення  = 77 см/c². Визначити амплітуду зміщення А і циклічну частоту ω коливань частинки.
= 77 см/c². Визначити амплітуду зміщення А і циклічну частоту ω коливань частинки.
Відповідь: А = 6,28 см; ω = 3,5 с-1.
314. Матеріальна точка виконує коливання уздовж деякого напрямку за законом  , де ω = 1,57 c-1. Амплітуда швидкості
, де ω = 1,57 c-1. Амплітуда швидкості 
 . Знайти для моментів часу
. Знайти для моментів часу  ,
,  ,
,  значення координати х, швидкості
значення координати х, швидкості  і прискорення а точки.
і прискорення а точки.
Відповідь: х1 = 0; х2 = 0,042м; х3 = 0,06 м; υ1 = 0,094 м/с; υ2 = 0,066 м/с; υ3 = 0; а1 = 0; а2 = 0,1 м/с2; а 3 = 0,15 м/с2.
315. Матеріальна точка виконує гармонічні коливання. Найбільше зміщення точки дорівнює 0,1 м, найбільша швидкість 0,2 м/с. Знайти циклічну частоту коливань і максимальне прискорення точки.
Відповідь: ω = 2 с-1; амах. = 0,4м/с2.
316. Коливання матеріальної точки масою 0,1 г відбуваються за законом:  (см). Визначити максимальні значення кінетичної енергії і сили, яка повертає матеріальну точку до положення рівноваги.
(см). Визначити максимальні значення кінетичної енергії і сили, яка повертає матеріальну точку до положення рівноваги.
Відповідь: Kмах = 4,9.10-6 Дж; Fмах = 1,97.10-4 Н.
317. До спіральної пружини підвісили тягарець, у результаті чого пружина розтяглася на 9 см. Який буде період коливань тягарця, якщо його трохи відтягнути від положення рівноваги, а потім відпустити?
Відповідь: Т = 0,6 с.
318. Матеріальна точка виконує прямолінійні гармонічні коливання. Період коливань Т = 2 с, а амплітуда А = 4 см. Знайти швидкість  точки у момент часу, коли її зміщення від положення рівноваги х = 2 см.
точки у момент часу, коли її зміщення від положення рівноваги х = 2 см.
Відповідь: υ = 0,108 м/с.
319. Матеріальна точка виконує прямолінійні гармонічні коливання. Циклічна частота ω = 4 c-1, амплітуда прискорення  = 72 см/c². Визначити швидкість
= 72 см/c². Визначити швидкість  точки у момент часу, коли її зміщення від положення рівноваги х = 2,2 см.
точки у момент часу, коли її зміщення від положення рівноваги х = 2,2 см.
Відповідь: υ = 0,157 м/с.
320. Частинка виконує прямолінійні гармонічні коливання. При зміщенні частинки від положення рівноваги на x1 = 2,6 см її швидкість  1 = 2,9 см/с, а при зміщенні на x2 = 3,4 см швидкість частинки
1 = 2,9 см/с, а при зміщенні на x2 = 3,4 см швидкість частинки  2 = 1,9 см/с. Визначити амплітуду зміщення А і циклічну частоту
2 = 1,9 см/с. Визначити амплітуду зміщення А і циклічну частоту  коливань частинки.
коливань частинки.
Відповідь: А = 0,0389 м; ω = 1 с-1.
321. Частинка одночасно бере участь у двох гармонічних коливаннях одного напрямку: x1 = 4cos4πt (см) і x2 = 3cоs(4πt + π/2) (см). Визначити циклічну частоту ω, амплітуду А і початкову фазу  результуючого коливання частинки. Побудувати векторну діаграму.
результуючого коливання частинки. Побудувати векторну діаграму.
Відповідь: ω = 4π с-1; А = 0,05 м; φ = 36,86о.
322. Написати рівняння руху x(t) частинки, яка одночасно бере участь у двох гармонічних коливаннях одного напрямку: x1 = 30cosπt/3 і x2 = 30cos(πt/3 + π/6) мм.
323. Додаються два гармонічних коливання одного напрямку: x1 = 20cosωt (мм) і x2 = 20cos(ωt + π/3) (мм). Визначити амплітуду А і початкову фазу  результуючого коливання, якщо ω = π с-1. Написати також рівняння результуючого коливання x(t).
результуючого коливання, якщо ω = π с-1. Написати також рівняння результуючого коливання x(t).
Відповідь: А=34,6 мм: φ = π/6.
324. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = sin  t (мм) і y = cos
t (мм) і y = cos  (t + 0,5) (мм). Знайти рівняння траєкторії точки y(x) та побудувати його графік.
(t + 0,5) (мм). Знайти рівняння траєкторії точки y(x) та побудувати його графік.
325. Частинка бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = 0,50sinωt і y = 1,5cosωt. Знайти рівняння руху частинки y(x). Побудувати графік результуючого траєкторії коливань і вказати на ній напрямок руху частинки.
326. Визначити амплітуду і початкову фазу результуючого коливання, утвореного при додаванні двох коливань однакового напрямку і періоду:
x1 = 10sin3πt (см) і x2 = 12sin(3πt +  /2) (см). Написати рівняння результуючого коливання. Побудувати векторну діаграму.
/2) (см). Написати рівняння результуючого коливання. Побудувати векторну діаграму.
Відповідь: А = 15,6 см; φ = 39,8о.
327. Зміщення освітленої точки на екрані осцилографа є результатом додавання двох взаємно перпендикулярних коливань, які описуються рівняннями: x = 1,5sin2πt см і y = 3sin2πt см. Написати рівняння результуючого коливання y(x) і побудувати його траєкторію.
327. Додаються два гармонічних коливання одного напрямку з однаковими періодами Т1 = Т2 = 1,5 с і амплітудами А1 = А2 = 2 см. Початкові фази коливань φ1 = π/2, φ2 = π/3. Визначити амплітуду А і початкову фазу  результуючого коливання. Знайти його рівняння і побудувати з дотриманням масштабу діаграму додавання амплітуд.
результуючого коливання. Знайти його рівняння і побудувати з дотриманням масштабу діаграму додавання амплітуд.
Відповідь: А= 3,86 см; φ = 75о.
329. Точка рухається в площині x y за законом x = Asinωt і y = Bcosωt, де А = В = 10 см,  = 2,0 рад/с. Знайти рівняння траєкторії руху точки y(x) і її прискорення у момент часу 2 с.
= 2,0 рад/с. Знайти рівняння траєкторії руху точки y(x) і її прискорення у момент часу 2 с.
Відповідь: а = 0,4 м/с2.
330. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = 5cosπt см і y = 10cosπt см. Знайти рівняння траєкторії точки y(х) і швидкість точки в момент часу 1 с.
Відповідь: υ = 0.
331. Частинка виконує прямолінійні згасаючі коливання з періодом Т = 4,5 с. Початкова амплітуда коливань Ao = 0,16 м, а амплітуда після 20 – ти повних коливань А = 0,01 м. Визначити коефіцієнт згасання β і логарифмічний декремент згасання  . Написати рівняння коливань частинки, прийнявши початкову фазу коливань
. Написати рівняння коливань частинки, прийнявши початкову фазу коливань  = 0.
= 0.
Відповідь: β = 0,03 с-1; δ = 0,135.
332. Математичний маятник довжиною l = 1 м виконує згасаючі коливання в середовищі, логарифмічний декремент згасання якого  1 = 1,26. Визначити логарифмічний декремент згасання
1 = 1,26. Визначити логарифмічний декремент згасання  2 маятника, якщо опір середовища зросте в 2 рази.
2 маятника, якщо опір середовища зросте в 2 рази.
Відповідь: δ2 = 2,52.
333. Знайти коефіцієнт згасання β і логарифмічний декремент згасання  математичного маятника, якщо відомо, що за час τ = 100 с коливань повна механічна енергія маятника зменшилася в десять разів. Довжина маятника l = 0,98 м.
математичного маятника, якщо відомо, що за час τ = 100 с коливань повна механічна енергія маятника зменшилася в десять разів. Довжина маятника l = 0,98 м.
Відповідь: β=0,0115 с-1;  = 0,023.
= 0,023.
334. Тіло масою m = 12 г виконує згасаючі коливання з частотою
ω = 3,14 c-1. При цьому за час τ = 60 с тіло втрачає 0,9 своєї повної механічної енергії. Знайти: а) коефіцієнт згасання β; б) коефіцієнт опору середовища r.
Відповідь: β = 0,019 с-1; r = 4,56.10-4 кг/с.
335. Амплітуда згасаючих коливань маятника за час t1 = 5 хв. зменшилася у 2 рази. За який час, від початкового моменту, амплітуда зменшилася у вісім разів?
Відповідь: t2 = 15 хв.
336. Енергія згасаючих коливань маятника, які відбуваються у деякому середовищі, протягом 120 с зменшилася у 100 разів. Визначити коефіцієнт опору середовища, якщо маса маятника дорівнює 0,2 кг.
Відповідь: r = 0,0076 кг/с.
337. Знайти логарифмічний декремент згасання математичного маятника довжиною 50 см, якщо за проміжок часу 5 хв. його повна механічна енергія зменшилася в 4·104 разів.
Відповідь: δ = 0,025.
338. Знайти число повних коливань системи, протягом яких енергія системи зменшилася у 2 рази. Логарифмічний декремент згасання  = 0,01.
= 0,01.
Відповідь: N = 34,6.
339. Тіло масою 5·10-3 кг виконує згасаючі коливання. Протягом часу τ= 50 с тіло втратило 60% своєї енергії. Визначити коефіцієнт опору середовища.
Відповідь: r = 9,16.10-5 кг/с.
340. Визначити період згасаючих коливань, якщо період власних коливань системи дорівнює 1 с, а логарифмічний декремент згасання дорівнює  = 0,628.
= 0,628.
Відповідь: Т = 1,005 с.
341. Складаються два взаємно перпендикулярних коливання, що описуються рівняннями х = А1 sin ωt і y = А2cosω(t+ τ), де А1 = 2 см; A2 = 1 см; ω= π с -1; τ = 0,5 с. Знайти рівняння траєкторії і побудувати її, зазначивши напрямок руху точки.
Відповідь:  або
або  .
.
342. Амплітуда згасаючих коливань маятника за час τ 1 = 2хв зменшилася у три рази. За який час τ 2, рахуючи від початкового моменту, амплітуда зменшиться у десять разів?
Відповідь: τ 2= 4,18 хв.
343. Амплітуда коливань маятника довжиною l = 1м за час τ = 10 хв. зменшилася у два рази. Визначити логарифмічний декремент коливань  .
.
Відповідь:  .
.
344. Гиря масою m = 500 г підвішена до спіральної пружини жорсткістю k = 20 Н/м і виконує пружні коливання у деякому середовищі. Логарифмічний декремент коливань  = 0,004. Визначити кількість N повних коливань, які повинна виконати гиря, щоб амплітуда коливань зменшилася в n = 2 рази. Коефіцієнт опору середовища дорівнює r = 4.10-3 кг/с. За який час τ відбудеться це зменшення?
= 0,004. Визначити кількість N повних коливань, які повинна виконати гиря, щоб амплітуда коливань зменшилася в n = 2 рази. Коефіцієнт опору середовища дорівнює r = 4.10-3 кг/с. За який час τ відбудеться це зменшення?
Відповідь:  ;
;  .
.
345. Визначити період То власних коливань, якщо період T згасаючих коливань системи дорівнює 2с і логарифмічний декремент згасань  = 0,628.
= 0,628.
Відповідь: Т = 1,96 с.
346. Знайти кількість N повних коливань системи, протягом яких енергія системи зменшилася в n = 2 рази. Логарифмічний декремент коливань  = 0,01.
= 0,01.
Відповідь: N = 35.
347. Вагон масою m = 80 т має чотири ресори. Жорсткість k пружин кожної ресори дорівнює 500 кН/м. При якій швидкості υ вагон почне сильно розгойдуватися внаслідок поштовхів на стиках рейок, якщо довжина l рейки дорівнює 12,8 м?
Відповідь:  .
.
348. Визначити амплітуду А і початкову фазу φ результуючого коливання, що виникає при додаванні двох коливань однакових напрямків і періодів: х1 =А1 sinωt і х2=A2 sin ω(t + τ), де А1= А2 = 1см; ω = π с-1; τ = 0,5 с. Знайти рівняння результуючого коливання.
Відповідь: A = 1,41 см;  ;
;  .
.
349. Точка бере участь одночасно у двох гармонічних коливаннях, що відбуваються у взаємно перпендикулярних напрямках і описуються рівняннями х = А1 cos ωt і y = А2 cos ω(t+τ), де А1 = 4 см; А2 = 8 см; ω = π с -1; τ = 1 с. Знайти рівняння траєкторії точки і побудувати графік її руху.
Відповідь:  або
або  .
.
350. За час t = 8 хв. амплітуда згасаючих коливань маятника зменшилася у три рази. Визначити коефіцієнт згасання β.
Відповідь: β = 0,0023 с-1.
351. Логарифмічний декремент коливань δ маятника дорівнює 0,003. Визначити кількість N повних коливань, які повинен виконати маятник, щоб їх амплітуда зменшилася у два рази.
Відповідь:  .
.
352. Тіло масою m = 15 г бере участь у згасаючих коливаннях. Протягом часу t = 30 с тіло втратило 50% своєї енергії. Визначити коефіцієнт згасання середовища  .
.
Відповідь:  = 0,0115с-1.
= 0,0115с-1.
353. Тіло масою m = 1 кг міститься у в’язкому середовищі з коефіцієнтом опору r = 0,05 кг/с. За допомогою двох однакових пружин жорсткістю k = 50 Н/м кожне тіло утримується в положенні рівноваги, пружини при цьому недеформовані. Тіло змістили від положення рівноваги і відпустили. Визначити: а) коефіцієнт згасання β; б) частоту v коливань; в) логарифмічний декремент коливань δ; г) кількість N коливань, після яких амплітуда зменшиться в е разів.
Відповідь: а) β = 0,025с-1; б) v = 1,59 Гц; в) δ = 0,0157; г) N = 64.
354. Коливальна система бере участь у згасаючих коливаннях з частотою v = 1000 Гц. Визначити частоту v0 власних коливань, якщо резонансна частота vpeз = 998 Гц.
Відповідь: v0 = 1002 Гц.
355. Визначити, наскільки резонансна частота відрізняється від частоти v0 = 1 кГц власних коливань системи, що характеризується коефіцієнтом згасання β = 400 с-1.
Відповідь:  .
.
356. При незмінній амплітуді змушувальної сили, амплітуда вимушених коливань при частотах ν1 = 100 с-1 і ν2 = 200 с-1 виявилася однаковою. Знайти резонансну частоту.
Відповідь: νрез. = 122,5 Гц.
357. Визначити, на скільки резонансна частота відрізняється від частоти  = 900 Гц власних коливань системи, яка характеризується коефіцієнтом згасання, рівним β = 500 с-1.
= 900 Гц власних коливань системи, яка характеризується коефіцієнтом згасання, рівним β = 500 с-1.
Відповідь: Δν = 7 Гц.
358. Визначити логарифмічний декремент  згасання коливань коливальної системи, для якої резонанс спостерігається при частоті, меншій власної частоти на 2 Гц. Власна частота коливань системи дорівнює ν0 = 10 кГц.
згасання коливань коливальної системи, для якої резонанс спостерігається при частоті, меншій власної частоти на 2 Гц. Власна частота коливань системи дорівнює ν0 = 10 кГц.
Відповідь: δ = 0,09.
359. Пружинний маятник (жорсткість пружини якого дорівнює k =10 Н/м, маса тягарця 0,1 кг) виконує змушені коливання у в’язкому середовищі з коефіцієнтом опору r = 2·10-2 кг/с. Визначити коефіцієнт згасання і резонансну амплітуду, якщо амплітудне значення змушувальної сили дорівнює 10-3 Н.
Відповідь: β = 0,1 с-1; Арез . =  м.
м.
360. У скільки разів амплітуда вимушених коливань менша резонансної амплітуди, якщо частота змушувальної сили у 2 рази більша резонансної частоти, а коефіцієнт згасання в обох випадках дорівнює 0,1  о (
о ( о – циклічна частота власних коливань)?
о – циклічна частота власних коливань)?
Відповідь: Арез./А = 15.
361. Коливальний контур радіоприймача складається з котушки індуктивністю 100 мГн і змінного конденсатора, ємність якого може змінюватися в межах від 9,7 до 92 пФ. У якому діапазоні довжин хвиль може працювати цей радіоприймач?
Відповідь: λ1 = 1855,5 м; λ2 = 5714,4 м.
362. Плоский конденсатор складається з двох круглих пластин діаметром 8 см. Між пластинами затиснута скляна пластинка ( = 6) товщиною 5 мм. Обкладки конденсатора замкнуті через котушку з індуктивністю 0,02 Гн. Визначити частоту коливань, яка виникає у цьому контурі.
= 6) товщиною 5 мм. Обкладки конденсатора замкнуті через котушку з індуктивністю 0,02 Гн. Визначити частоту коливань, яка виникає у цьому контурі.
Відповідь: ν = 1,55.105 Гц.
363. Коливальний контур складається з котушки індуктивністю 0,003 Гн і плоского конденсатора. Пластини конденсатора у вигляді дисків радіусом 1,2 см розташовані на відстані 0,3 мм одна від одної. Яким буде період коливань, якщо конденсатор заповнити діелектриком з діелектричною проникністю  = 4?
= 4?
Відповідь: Т = 1,256.10-6 с.
364. Котушка індуктивністю 30 мкГн приєднана до плоского конденсатора з площею пластин 0,01 м2 і відстанню між ними 0,1 мм. Знайдіть діелектричну проникність середовища, яке заповнює простір між пластинами, якщо контур налаштований на частоту 400 кГц.
Відповідь: ε = 6.
365. Максимальна напруга в коливальному контурі, який складається з котушки індуктивністю 5 мкГн і конденсатора ємністю 1330 пФ, дорівнює 1,2 В. Опір котушки безмежно малий. Визначити максимальне значення сили струму в контурі.
Відповідь: Імах = 0,02 А.
366. На конденсаторі, ввімкнутому в коливальний контур, максимальна напруга дорівнює 100 В. Ємність конденсатора 10 пФ, індуктивність 1,6 мГн. Напишіть рівняння залежності електричної і магнітної енергії в контурі. Визначити максимальне значення сили струму в контурі.
Відповідь: Імах = 7,9.10-3 А.
367. У коливальному контурі індуктивність котушки дорівнює 0,2 Гн. Амплітуда сили струму 40 мА. Знайдіть енергію магнітного поля котушки й енергію електричного поля конденсатора в момент, коли миттєве значення сили струму в 2 рази менше амплітудного. Опором у контурі знехтувати.
Відповідь: We = 1,2.10-4 Дж; Wм = 0,4.10-4 Дж.
368. Коливальний контур складається із котушки індуктивністю 4 Гн і конденсатора ємністю 1 мкФ. Амплітуда коливань заряду на обкладках конденсатора дорівнює 100 мкКл. Визначити максимальне значення напруги на обкладках конденсатора і максимальне значення струму в котушці.
Відповідь: Імах = 5.10-2 А; Uмах = 100 В.
369. Коливальний контур містить конденсатор ємністю С = 8 пФ і котушку індуктивністю L = 0,5 мГн. Опором контура знехтувати. Яка максимальна напруга Umax на обкладках конденсатора, якщо максимальна сила струму в контурі Imax = 40 мА?
Відповідь: Uмах = 316 В.
370. Котушка (без сердечника) довжиною l = 50 см і перерізом S1 = 3 см² має N = 1000 витків і з'єднана паралельно з конденсатором. Площа кожної пластини конденсатора S2 = 75 см², відстань між пластинами d = 5 мм, діелектрик – повітря. Знехтувавши активним опором контура, знайти період Т його коливань.
Відповідь: Т = 6,26.10-7 с.
371. Знайти відношення енергії магнітного поля до енергії електричного поля для моменту часу t = T/8, вважаючи, що коливальні процеси відбуваються у ідеальному коливальному контурі.
Відповідь: Wм/We = 1.
372. Ємність коливального контуру 1,0 мкФ, а індуктивність 10 мГн. Який омічний опір потрібно ввімкнути в коло, щоб зменшити резонансну частоту незатухаючих коливань на 0,01%?
Відповідь: R = 2,0 Ом;
373. На яку довжину хвилі буде резонувати контур, який складається з котушки індуктивністю 4 мкГн і конденсатора ємністю 1,11 нФ?
Відповідь: λ = 125,5 м.
374. Котушка, індуктивність якої L = 30 мкГн, приєднана до плоского конденсатора. Площа кожної пластини S = 100 см2, відстань між ними d = 0,1 мм. Визначити діелектричну проникність  середовища, яке заповнює простір між пластинами, якщо контур резонує на монохроматичну електромагнітну хвилю, довжина якої
середовища, яке заповнює простір між пластинами, якщо контур резонує на монохроматичну електромагнітну хвилю, довжина якої  = 750 м.
= 750 м.
Відповідь: ε = 6.
375. На яку довжину хвилі  налаштований коливальний контур радіоприймача, якщо він має індуктивність L = 1,5 мГн і ємністю С = 0,67 нФ? Активним опором контуру знехтувати.
налаштований коливальний контур радіоприймача, якщо він має індуктивність L = 1,5 мГн і ємністю С = 0,67 нФ? Активним опором контуру знехтувати.
Відповідь: λ = 1888,7 м.
376. Задано рівняння плоскої хвилі U(x, t) = A cos (ωt - kx), де А = 0,5 см;  = 628 с-1; k = 2 м-1. Визначити: а) частоту коливань v і довжину хвилі λ; б) фазову швидкість υ; в) максимальні значення швидкості υmax і прискорення аmах коливань частинок середовища.
= 628 с-1; k = 2 м-1. Визначити: а) частоту коливань v і довжину хвилі λ; б) фазову швидкість υ; в) максимальні значення швидкості υmax і прискорення аmах коливань частинок середовища.
Відповідь: а) 100 Гц, 3,14 м; б) 314 м/с; в) 3,14 м/с, 1972 м/с2.
377. Плоска звукова хвиля має період Т= 3 мс, амплітуду A = 0,2 мм і довжину хвилі λ = 1,2 м. Для точок середовища, віддалених від джерела коливань на відстань х =2 м, знайти: а) зміщення U(х, t) у момент t = 7 мс; б) швидкість υ і прискорення a для того самого моменту часу. Початкову фазу коливань прийняти рівною нулю.
Відповідь: а) – 0,1 мм; б) 0,00254 м/с, 0,0429 кг/с2.
378. Визначити різницю фаз  коливань джерела хвиль, що містяться у пружному середовищі, і точки цього середовища, віддаленої на х = 2 м від джерела. Частота v коливань дорівнює 5 Гц; хвилі поширюються зі швидкістю υ = 40 м/с.
коливань джерела хвиль, що містяться у пружному середовищі, і точки цього середовища, віддаленої на х = 2 м від джерела. Частота v коливань дорівнює 5 Гц; хвилі поширюються зі швидкістю υ = 40 м/с.
Відповідь: 1,57 рад.
379. Знайти швидкість υ звуку в повітрі при температурах Т1 = 290 К і Т2 = 350 К.
Відповідь: 339 м/с; 375 м/с.
380. Є два джерела, що створюють коливання в однаковій фазі і збуджують у навколишнім середовищі плоскі хвилі однакової частоти і амплітуди (А1= А2 = 1 мм). Знайти амплітуду А коливань точки середовища, віддаленої від одного джерела коливань на відстань х1 = 3,5 м і від іншого – на х2 = 5,4 м. Напрямки коливань у розглянутій точці збігаються. Довжина хвилі λ = 0,6 м.
Відповідь: 1,73 мм.
381. У трубі довжиною l = 1,2 м міститься повітря при температурі
Т = 300 К. Визначити мінімальну частоту  можливих коливань повітряного стовпа у двох випадках: а) труба відкрита; б) труба закрита.
можливих коливань повітряного стовпа у двох випадках: а) труба відкрита; б) труба закрита.
Відповідь: а ) 144 Гц; б) 72 Гц.
382. Звукові коливання, що мають частоту v = 0,5 кГц і амплітуду A = 0,25 мм, поширюються у пружному середовищі. Довжина хвилі λ=70 см. Знайти: а) швидкість υ поширення хвиль; б) максимальну швидкість  частинок середовища.
частинок середовища.
Відповідь: а) 350 м/с; б) 0,79 м/с.
383. Від джерела коливань поширюється хвиля вздовж прямої лінії. Амплітуда А коливань дорівнює 10 см. Наскільки велике зміщення точки, віддаленої від джерела на х =3/4λ, у момент, коли від початку коливань минув час t = 0,9 T?
Відповідь: 5,88 см.
384. Спостерігач, який перебуває на відстані l = 800 м від джерела звуку, чує звук, що надійшов по повітрю, на Δt = 1,78 с пізніше, ніж звук, що долинув по воді. Знайти швидкість υ звуку у воді, якщо температура T повітря дорівнює 290 К.
Відповідь: 1,413 км/с.
385. Знайти відношення швидкостей υ1/υ2 звуку у водні і вуглекислому газі при однаковій температурі газів.
Відповідь: 4,81.
386. Стояча хвиля утворюється при накладанні біжучої хвилі, і хвилі, відбитої від межі поділу середовищ, перпендикулярної її напрямку поширення. Знайти положення (відстань від межі поділу середовищ) вузлів і пучностей стоячої хвилі, якщо відбивання відбувається: а) від середовища з меншою густиною; б) від середовища з більшою густиною. Швидкість υ поширення звукових коливань дорівнює 340м/с і частота v = 3,4 кГц.
Відповідь:  ; lвузл = 2,5; 7,5; 12,5 см,...; lпучн = mυ/2ν;
; lвузл = 2,5; 7,5; 12,5 см,...; lпучн = mυ/2ν;
lпучн = 0.5; 10 см,...; 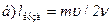 ; lвузл = 0,5; 10 см,...; lпучн = (2m+1)υ/4ν; lпучн = 2,5; 7,5; 12,5 см,....
; lвузл = 0,5; 10 см,...; lпучн = (2m+1)υ/4ν; lпучн = 2,5; 7,5; 12,5 см,....
387. Визначити довжину λ біжучої хвилі, якщо в стоячій хвилі відстань l між: а) першою і сьомою пучностями дорівнює 15 см, б) першим і четвертим вузлом дорівнює 15 см.
Відповідь: а) 5см; б) 10 см.
388. Поперечна хвиля поширюється уздовж пружної мотузки зі швидкістю 15 м/с. Період коливань дорівнює 1,2 с, амплітуда – 2 м. Визначити довжину хвилі, фазу коливань, зміщення точок від положення рівноваги, які перебувають на відстані 45 м від джерела хвиль у момент часу t = 4 с.
Відповідь: λ = 18 м; Ф = 5,23 рад; uх,t = 1,99 м або uх,t = 0,18 м.
389. Хвиля з періодом 1,6 с і амплітудою коливань 8 см поширюється зі швидкістю 25 м/с. Чому дорівнює зміщення точок від положення рівноваги на відстані 75 см від джерела хвиль, у той момент часу, коли від початку коливань джерела пройшов час 2 с? Чому дорівнює швидкість коливань цієї точки?
Відповідь: uх,t = 0,079 м;  = 0 м/с.
= 0 м/с.
390. Звукові коливання, які мають частоту 500 Гц і амплітуду 0,25 мм, поширюються у пружньому середовищі. Довжина хвилі – 0,7 м. Знайти:
а) швидкість поширення хвиль, б) максимальну швидкість коливань частинок у середовищі.
Відповідь: υ = 350 м/с; 
391. Швидкість звуку у воді – 1450 м/с. Джерело коливань, що знаходиться у воді, має частоту 200 Гц. Визначити: а) довжину звукової хвилі у воді; б) відстань між найближчими точками, що виконують коливання в протилежних фазах; в) різницю фаз коливань у двох точках, що знаходяться на відстані 1 м.
Відповідь: λ = 7,25 м; Δх = 3,625 м; ΔФ = 0,866 рад.
392. Хвиля поширюється у пружному середовищі зі швидкістю 100 м/с. Найменша відстань між точками середовища, фази коливань яких протилежні, дорівнює 1 м. Визначити: а) частоту коливань; б) максимальне значення швидкості коливань точок середовища, якщо амплітуда коливань дорівнює 5 см.
Відповідь: ν = 50 Гц;  = 15,7 м/с.
= 15,7 м/с.
393. Рівняння плоскої хвилі має вигляд  м. Визначити: а) частоту коливань і довжину хвилі; б) фазову швидкість;
м. Визначити: а) частоту коливань і довжину хвилі; б) фазову швидкість;
в) максимальне значення швидкості і прискорення коливань частинок середовища.
Відповідь: ν = 100 Гц; λ = 3,14 м; υ = 314 м/с; 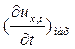 =- 3,14 м/с;
=- 3,14 м/с; 
394. Плоска пружна хвиля поширюється уздовж лінії, яка з'єднує дві точки, відстань між якими Δr = 0,15 м. Визначити довжину хвилі λ і різницю фаз Δφ коливань частинок середовища в цих точках, якщо частота джерела ν = 10³ Гц, а фазова швидкість хвилі  = 340 м/с. Записати рівняння хвилі, якщо амплітуда А = 2 см.
= 340 м/с. Записати рівняння хвилі, якщо амплітуда А = 2 см.
Відповідь: λ = 0,340 м; Δφ = 2,77 рад.
395. Звукові коливання, які мають частоту  = 0,5 кГц і амплітуду А = 0,25 мм, поширюються у пружному середовищі. Довжина хвилі λ = 0,7 м. Знайти: а) фазову швидкість
= 0,5 кГц і амплітуду А = 0,25 мм, поширюються у пружному середовищі. Довжина хвилі λ = 0,7 м. Знайти: а) фазову швидкість  поширення хвиль; б) максимальну швидкість частинок середовища.
поширення хвиль; б) максимальну швидкість частинок середовища.
Відповідь: υ = 350 м/с;  = 0,785 м/с.
= 0,785 м/с.
396. Скласти рівняння плоскої хвилі, яка поширюється у повітрі, частинки якої коливаються з частотою 2000 Гц і амплітудою 1,7 мкм. Фазова швидкість поширення хвилі 340 м/с. Визначити також середнє значення густини енергії хвильового руху, якщо густина повітря дорівнює 1 кг/м3.
Відповідь: 
397. Механічні коливання частотою 400 Гц і амплітудою зміщення 25 мм поширюються у повітрі уздовж циліндричної труби зі швидкістю  = 340 м/с. Записати рівняння хвилі. Визначити довжину хвилі, максимальну швидкість частинок повітря, середню густину енергії. Густина повітря дорівнює 1 кг/м³.
= 340 м/с. Записати рівняння хвилі. Визначити довжину хвилі, максимальну швидкість частинок повітря, середню густину енергії. Густина повітря дорівнює 1 кг/м³.
Відповідь: λ = 0,85 м;  = 62,8 м/с;
= 62,8 м/с;  = 1972 Дж/м3.
= 1972 Дж/м3.
398. Котушка індуктивністю L = 1 мГн і повітряний конденсатор, який складається з двох круглих пластин діаметром D = 20см кожна, з’єднані паралельно. Відстань d між пластинами дорівнює 1 см. Визначити період Т коливань.
Відповідь:  с.
с.
399. Коливальний контур складається з котушки індуктивності L = 1,6 мГн і конденсатора ємністю C = 0,04 мкФ. Визначити максимальну силу струму Іmax в контурі, якщо максимальна напруга  на клемах конденсатора дорівнює 200 В. Опором контуру знехтувати.
на клемах конденсатора дорівнює 200 В. Опором контуру знехтувати.
Відповідь: 1 А.
400. Котушка (без сердечника) довжиною l = 6 0 см і площею S1 перерізу, яка дорівнює 5 см2, має N = 2000 витків і з'єднана паралельно з конденсатором. Конденсатор складається із двох пластин площею S2 = 10 см2 кожна. Відстань d між пластинами дорівнює 5 мм. Діелектрик –скло (ε =6). Визначити період Т коливань контура.
Відповідь: 10,5 нс.
401.Індуктивність L коливального контуру дорівнює 0,5 мГн. Яка повинна бути електроємність С контуру, щоб він резонував на довжину хвилі λ = 300 м?
Відповідь: 51 пФ.
402. Для демонстрації дослідів Герца із заломленням електромагнітних хвиль іноді беруть велику призму, виготовлену з парафіну. Визначити показник заломлення парафіну, якщо його діелектрична проникність  = 2 і магнітна проникність
= 2 і магнітна проникність  = 1.
= 1.
Відповідь: 1,41.
403.Два паралельних провідники, які занурені в гліцерин, індуктивно з'єднані з генератором електромагнітних коливань частотою  = 420 МГц. Відстань l між пучностями стоячих хвиль на провідниках дорівнює 7 см. Знайти діелектричну проникність ε гліцерину. Магнітну проникність μ середовища прийняти за одиницю.
= 420 МГц. Відстань l між пучностями стоячих хвиль на провідниках дорівнює 7 см. Знайти діелектричну проникність ε гліцерину. Магнітну проникність μ середовища прийняти за одиницю.
Відповідь: 26.
404.Конденсатор електроємністю С = 500 пФ, з'єднанийпаралельно з котушкою довжиною l = 40 см і площею перерізу S, яка дорівнює 5 см2. Котушка має N = 1000 витків. Сердечник немагнітний. Знайти період T коливань.
Відповідь:  мкс.
мкс.
405. Коливальний контур має котушку індуктивністю L = 0,5 мГн. Максимальна напругана обкладках конденсатора Umax=317 В, а максимальна сила струму Ітаx = 40 мА. Знайти ємність конденсатора.
Відповідь: С = 8 пФ.
406. На яку частоту ν буде резонувати контур, який складається із котушки індуктивністю L = 4 мкГн і конденсатора електроємністю С = 1,11 нФ?
Відповідь: 2,39.106 Гц.
ІНТЕРФЕРЕНЦІЯ СВІТЛА
Основні формули
1. Швидкість поширення світла в середовищі

де с – швидкість світла в вакуумі;
n – показник заломлення середовища.
2. Оптична довжина ходу променя
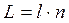 ,
,
де l – геометрична довжина ходу променя в середовищі з показником заломлення n.
3. Оптична різниця ходу двох променів

4. Зв’язок оптичної різниці ходу з різницею фаз

де  – хвильове число;
– хвильове число;
 – довжина хвилі світла.
– довжина хвилі світла.
5. Умова максимуму інтерференції когерентних хвиль
 ,
,
де k = 1, 2, 3,... – порядок максимуму;
 довжина хвилі.
довжина хвилі.
6. Умова мінімуму інтерференції когерентних хвиль

де k = 1, 2, 3,... – порядок мінімуму.
7. Ширина інтерференційної смуги в досліді Юнга

де L – відстань від екрана до щілин Юнга;
d – відстань між щілинами Юнга;
 – довжина хвилі.
– довжина хвилі.
8. Оптична різниця ходу променів в тонких плівках:
а) відбиті промені
 або
або 
б) прохідні промені

 або
або 

де d – товщина плівки;
n – показник заломлення речовини плівки;
і1 і і2 – кути падіння і заломлення променів.
9. Радіуси світлих і темних кілець Ньютона:
а) відбиті промені



 – світлі кільця;
– світлі кільця;
 – темні кільця;
– темні кільця;
б) прохідні промені
 – cвітлі кільця;
– cвітлі кільця;
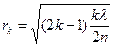 – темні кільця,
– темні кільця,
де k = 1, 2, 3,... – порядок кільця;
R – радіус кривизни плоско-oпуклої лінзи;
 – довжина хвилі світла;
– довжина хвилі світла;
n – показник заломлення речовини, якою заповнено простір між лінзою і плоскопаралельною пластинкою.






