Приклади розв’язування задач. Приклад 1. Точкове джерело світла з довжиною хвилі 0,6 мкм розміщене на відстані а = 100 см перед діафрагмою з круглим отвором радіусом rk = 1 мм

Приклад 1. Точкове джерело світла з довжиною хвилі 0,6 мкм розміщене на відстані а = 100 см перед діафрагмою з круглим отвором радіусом r_k = 1 мм. Визначити відстань b від хвильової поверхні до точки спостереження, для якої в отворі діафрагми вкладається k = 5 зон Френеля.

Дано:

l = 0,6 мкм

a = 1 м

k = 5

r_k = 1 мм

____________

b –?

	Рисунок 13

Розв’язування. Якщо в отворі діафрагми на хвильовій поверхні радіусом а вкладається k зон Френеля, то радіус k -ї зони буде рівний (рис.13):

 

.

Звідки

.

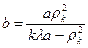Підставимо числові значення

 

= 0,5 м.

Відповідь: b = 0,5 м.

 

 

Приклад 2. На щілину шириною b = 0,01 мм перпендикулярно падає промінь світла (l = 577 нм). Під яким кутом j до початкового напрямку будуть спостерігатись максимуми другого і третього порядків?

 

Дано:

b = 0,01 мм

l = 577 нм

k₁ = 2

k₂ = 3

____________

j₁ –? j₂ –?

 

	Рисунок 14

Розв’язування. Умова максимумів дифракції на одній щілині має вигляд:

 

 

де bsinj = D – оптична різниця ходу двох крайніх променів, які проходять крізь щілину (рис.14).

Звідки

 

sin j = ± або j = arcsin .

Підставимо числові значення:

 

a) k = 2, j₂ = arcsin 8,1^о;

 

б) k = 3, j₃ = arcsin .

 

 

Відповідь: j ₂ = 8,1°; j ₃ = 11,6°.

 

 

Приклад 3. Дифракційна гратка містить 200 смуг на 1 мм. На гратку падає перпендикулярно монохроматичне світло з довжиною хвилі 0,6 мкм. Максимуми якого найбільшого порядку дає ця гратка?

 

Дано:

N = 200

l = 1 мм

l = 0,6 мкм

____________

k_max –?

	Рисунок 15

Розв’язування. Головні максимуми дифракції на дифракційній гратці (рис.15) спостерігаються згідно з умовою

 

d sin j = k l,

 

де dsinj = D – oптична різниця ходу двох суміжних променів;

k – порядок дифракційної смуги;

l – довжина хвилі світла.

Порядок дифракційної смуги з цієї умови дорівнює:

 

.

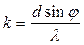Якщо sin j = 1, то k = k_max , тому

 

.

 

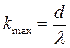Сталу дифракційної гратки знайдемо із умови

 

Тому

.

 

Підставимо числові значення

.

Відповідь: k_max = 8.

 

Приклад 4. За допомогою дифракційної гратки з періодом d = 20 мкм необхідно роздільно бачити дублет натрію (l₁ = 589,0 нм і l₂ = 589,6 нм) в спектрі другого порядку. При якій найменшій ширині гратки це можливо?

Дано:

d = 20 мкм

l₁ = 589,0 нм

l₂ = 589,6 нм

k = 2

____________

l –?

Розв’язування. Роздільна здатність дифракційної гратки визначається формулами:

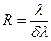i R = k N,

 

де k – порядок спектра;

N – число всіх щілин або смуг в гратці;

dl = l₁ – l₂ – найменший інтервал довжин хвиль, які можна бачити роздільно в околі довжин хвиль l₁.

Прирівняємо праві частини цих формул:

 

kN = .

 

Число всіх щілин в гратці дорівнює

 

N = ,

де l – ширина гратки;

d – стала гратки.

 

Тому

.

Звідки

,

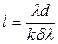або

.

 

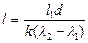Підставимо числові значення

 

м.

Відповідь: l @ 1 см.

ПОЛЯРИЗАЦІЯ СВІТЛА

Основні формули

 

1. Закон Брюстера

tg і = n_2,1,

 

де і – кут падіння променя;

n_2,1 – відносний показник заломлення.

2. Коефіцієнт відбивання падаючого променя:

 

,

Рисунок 16

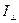де = , або

I₀ – інтенсивність природного променя.

3. Коефіцієнт заломлення променя:

 

,

 

де I_^ – інтенсивність променя з перпендикулярною орієнтацією вектора ;

 

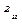– інтенсивність променя з паралельною орієнтацією вектора .

4. Ступінь поляризації заломленого променя

.

5. Закон Малюса

I = I₀ cos² a,

 

де I – інтенсивність поляризованого світла після аналізатора;

I₀ – інтенсивність світла до аналізатора;

a – кут між площинами поляризації поляризатора і аналізатора.

6. Ступінь поляризації частково поляризованого світла в довільному випадку:

,

 

де I_max i I_min – максимальна і мінімальна інтенсивності частково поляризованого світла, яке пропускається через аналізатор.

7. Різниця фаз поляризованих променів, яка створюється анізотропною пластинкою

 

,

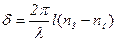де – хвильове число;

l – товщина анізотропної пластинки;

n₃ i n_н – показники заломлення відповідно звичайного і незвичайного променів в анізотропній пластинці;

 

8. Кут повертання площини поляризації монохроматичного світла при проходженні через оптично активну речовину:

а) в твердих тілах

j = [a] l;

 

в) в розчинах

j = [a] С l,

де [a] – питоме повертання площини поляризації;

C – масова концентрація оптично активної речовини в розчині;

l – довжина шляху, пройденого світлом в оптично активній речовині.

9. Виникнення оптичної різниці фаз в деяких штучно анізотропних речовинах:

а) у випадку механічних деформацій

 

,

де – хвильове число;

l – довжина тіла в напрямку створення механічних деформацій;

k₁ – стала величина, характеризує властивості певної речовини;

s – нормальна механічна напруга (s = ).

б) у випадку дії електричного поля (ефект Керра)

,

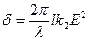де k₂ – стала величина;

E – напруженість електричного поля в комірці Керра.

в) у випадку дії магнітного поля

,

де k₃ – стала величина;

Н – напруженість магнітного поля.