Рух, при якому тіло за рівні проміжки часу здійснює різні переміщення, називається нерівномірним, або змінним.
При нерівномірному русі швидкість тіла з часом змінюється, тому для характеристики такого руху вводять поняття середньої і миттєвої швидкості.
Середньою швидкістю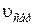 
нерівномірного прямолінійного руху називається швидкість, яка дорівнює відношенню усього пройденого шляху 
до усього часу 
.
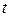. (3.1)
Миттєва швидкість - це швидкість тіла в даний момент часу в даній точці траєкторії.
Миттєва швидкість визначається межею, до якої наближається відношення вектора переміщення 
до проміжку часу 
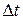, за який це переміщення відбулося, за умови, що 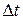наближається до нуля. У математиці цю величину називають похідною і позначають так:
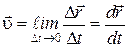. (3.2)
Зміну швидкості характеризує величина, яка називається прискоренням.
Прискорення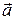 
-це векторна фізична величина, що дорівнює відношенню зміни швидкості 
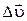до проміжку часу 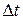, за який відбулася ця зміна.
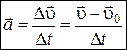, (3.3)
де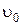 
- початкова швидкість, 
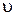- кінцева швидкість тіла в даний момент часу
(вектор а дорівнює дельта ве, поділений на дельта те).
.
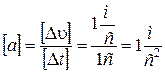1м/с2 - це прискорення такого руху, при якому за кожну секунду швидкість змінюється на 1м/с.
Прискорення є похідною за часом від швидкості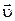 
, або другою похідною за часом від радіуса-вектора точки 
:
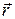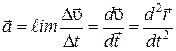. (3.4)
Рівнозмінний прямолінійний рух – церух, при якому величина та напрям прискорення не змінюються.
. (3.5)
Рівнозмінний рух може бути:
1 рівноприскореним, коли величина швидкості збільшується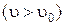 
, при цьому 
;
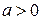2 рівносповільненим, коли величина швидкості зменшується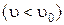 
, при цьому 
.
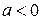4. Рух, траєкторія якого крива лінія, називають криволінійним. У криволінійному русі переміщення тіла не збігається з траєкторією його руху, тому модуль переміщення не дорівнює шляху. Прикладами криволінійного руху є рух тіла по колу, еліпсу, параболі, гіперболі.
Миттєва швидкість тіла в будь-якій точці криволінійної траєкторії напрямлена по дотичній до траєкторії в цій точці і визначається за формулою:
υ = lіm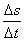 
= 
,
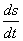де ∆s, ds - нескінченно мале переміщення тіла, коли воно проходить через дану точку, за нескінченно малий інтервал часу ∆t.
У криволінійному русі напрям швидкості завжди змінюється, тому тіло має нормальне прискорення, напрямлене перпендикулярно до швидкості в даній точці, тобто вздовж радіуса кривизни траєкторії. Модуль швидкості або сталий, або змінюється. Якщо модуль швидкості змінюється, тіло має тангенціальне прискорення. Повне прискорення при криволінійному русі дорівнює векторній сумі нормального і тангенціального прискорень. Модуль і напрям повного прискорення залежить від форми криволінійної траєкторії.
Прискорення — векторна величина. Його напрямок не завжди збігається із напрямком швидкості. В загальному випадку вектор прискорення утворює з вектором швидкості деякий кут і розкладається на дві складові. Складова вектора прискорення, яка направлена паралельно до вектора швидкості, а, отже, вздовж дотичної до траєкторії, називається тангенціальним прискоренням. Складова вектора прискорення, що направлена перпендикулярно до вектора швидкості, а, отже, вздовж нормалі до траєкторії, називаєтьсянормальним прискоренням.
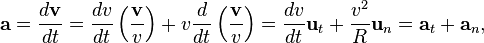
де R — радіус кривини лінії руху у точці, що розглядається.
Перший член у цій формулі задає тангенціальну складову прискорення (тангенціальне прискорення) і характеризує зміну швидкості за величиною. Другий — нормальна складова прискорення (нормальне, або доцентрове прискорення) і характеризує зміну швидкості за напрямом. Зміна напрямку одиничного вектора завжди перпендикулярна до цього вектора, тому другий член в цій формулі нормальний до першого.
Проекції вектора 
на напрям вектора швидкості і на напрям, перпендикулярний до вектора швидкості даються виразами:
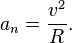
Слід зазначити, що часто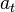 
і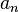 
(проекції відповідних векторів) називають тангенціальним прискоренням і нормальним прискоренням (як і відповідні вектори).
Модуль повного прискорення
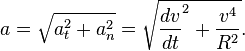
У загальному випадку обертового руху використовується поняття кутове прискорення, яке характеризує зміну кутової швидкості у часі і за аналогією до лінійного прискорення обчислюється за формулою:
Існує зв'язок між тангенціальним і кутовим прискореннями:
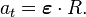
5. Кінематика – це розділ механіки, в якому вивчаються види механічного руху. Кінематика відповідає на питання: «Як рухається тіло?». Вона вивчає геометричні та математичні характеристики руху без дослідження його фізичних причин. Обертальним рухом твердого тіла називається такий рух, при якому залишаються нерухомими всі його точки, що лежать на деякій прямій, яка називається віссю обертання. Обертальне прискорення (дотичне) прискорення залежить від знаку алгебраїчної величини кутового прискорення тіла і радіусу обертання. Вектор обертального прискорення спрямований по дотичній до кола в напрямку обертання тіла, тобто за вектором швидкості точки. Кутове прискорення - похідна від кутової швидкості по часу
,
де 
- кутове прискорення,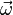 
- кутова швидкість, t - час.
Вимірюється в рад/c2.
6. Перший закон Ньютона (закон інерції)
Цей закон також має назву закону інерції або принципу Галілея. Строге його формулювання в сучасному викладі таке:
· Існують такі системи відліку, в яких центр мас будь-якого тіла, на яке не діють ніякі сили або рівнодійна діючих на нього сил дорівнює нулю, зберігає стан спокою аборівномірного прямолінійного руху, допоки цей стан не змінять сили, застосовані до нього.
Цей закон є спеціальним випадком другого закону Ньютона (дивись нижче), але його значення полягає в тому, що він визначає системи відліку, в яких справедливі наступні два закони. Ці системи відліку мають назву інерційних або Галілеєвих, тобто таких, які рухаються зі сталою швидкістю одна відносно іншої.
