Приклад. 1. З допомогою дисперсійного аналізу вивчіть тісноту та істотність зв’язку між кваліфікацією працівників та кількістю продаж деталей, вироблених за 1 годину, якщо відомі дані:
| Розряд | Число праців- ників у групі | Кількість деталей, вироблених за 1годину, шт. |
| V-VI | 10; 12; 11; 10; 12; 15. | |
| IV-III | 8; 6; 7; 10; 8. |
Розв’язання:
1. Знаходимо групові та загальну середню із залежної (результативної) ознаки – числа деталей, вироблених за 1 год.
| Розряд | Число робітників | Усього вироблено за 1 годину (yі) | Середній виробіток ( )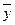
|
| V-VI | 11,67 | ||
| IV-III | 7,80 | ||
| разом | 9,90 |
2. Знаходимо дисперсії виробітку:
а) загальну: б 2=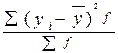 
б 2= 
б 2 = 6,08
Характеризує варіацію виробітку під впливом усіх факторів (причин).
б) міжгрупову: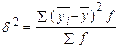 
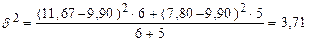
Характеризує варіацію виробітку під впливом лише рівня кваліфікації (розряду) – тобто ознаки, яка вивчається і є групувальною.
3. Знаходимо емпіричний коефіцієнт детермінації
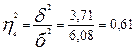
Значить на 61% варіація виробітку обумовлена зміною рівня кваліфікації, а на 39% - іншими причинами.
4. Тіснота зв’язку оцінюється за емпіричним кореляційним відношенням
значення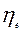 
>0,7 свідчить про тісний зв’язок між показниками.
5. Істотність (невипадковість) зв’язку оцінюють за F-критерієм Фішера
,
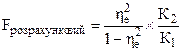де К2 = n – m
К1 = m – 1
m – число груп;
n – число обстежених одиниць.
Критичне, табличне значення F0,95 = 5,12
Fрозрахункове > Fтабличного, то
істотність зв’язку вважається доведеною.
Таблиця значення F-критерію Фішера при рівні значимості
a = 0,05
| n – m | m – 1 | ||||
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 |
Задачі і завдання для виконання на практичних заняттях
8.1. З допомогою дисперсійного аналізу вивчіть тісноту та істотність зв’язку між кваліфікацією працівників та кількістю продаж деталей, вироблених за 1 годину, якщо відомі дані:
| Розряд | Число праців- ників у групі | Кількість деталей, вироблених за 1годину, шт. |
| V-VI | 12; 14; 10; 12; 11; 12; 14; 13; 14; 15. | |
| IV-III | 6; 7; 8; 9; 10; 7; 7; 10; 11; 10; 8; 12; 10; 11; 8. |
8.2. За допомогою дисперсійного аналізу зробіть висновок про тісноту та істотність зв’язку між типом упаковки товару та попитом на нього. Дайте рекомендації щодо доцільності переходу заводу на нову упаковку. Використайте дані вибіркового дослідження:
| Тип упаковки | Кількість проданого за контрольний період товару на робочих місцях, які спостерігалися, шт. |
| Нова | 25; 24; 25; 26; 22; 24; 25; 26; 23; 24; 26; 25; 22; 23. |
| Традиційна | 22; 23; 22; 24; 25; 22; 24; 23; 22; 21; 20; 24; 20; 21. |
8.3. За умовою завдань 3.5.1. – 3.5.7. цього збірника виконайте дисперсійний та кореляційно-регресійний аналіз взаємозв’язку. Перевірте істотність та тісноту зв’язку. Напишіть письмові висновки.
8.4. Відомі дані по 10 фірмах, що мають однакові технологічні лінії:
| №№ фірми | ||||||||||
| Вік обладнання, років | ||||||||||
| Витрати на ремонт обладнання, тис. грн. | 1,5 | 2,7 | 3,6 | 2,0 | 2,9 | 3,7 | 3,0 | 2,3 | 3,1 | 4,0 |
Визначити параметри лінійного рівняння регресії, виконати аналіз зв’язку, оцінити його тісноту та істотність. Якщо фірма планує придбати подібну лінію, що була у вжитку 5 років, визначити прогнозовані витрати на ремонт обладнання за рік.
8.5. За емпіричними даними по 10 підприємствах вивчалася залежність між обсягами виконаних понадурочних робіт (тис. люд. год.) та кількістю випадків виробничих травм (одиниць).
Одержані розрахункові дані:
| х | У | х2 | у2 | ху | 
| |
| Суми S | 5,3037 |
Знайдіть параметри і запишіть лінійне рівняння регресії. Обчисліть коефіцієнт еластичності, зробіть висновки.
Обчисліть середньоквадратичну помилку моделі. Оцініть тісноту та істотність зв’язку.
