В межах цієї теми студент повинен засвоїти види і способи відбору одиниць із генеральної сукупності, способи поширення вибіркових характеристик на генеральну сукупність і методику обчислення середньої та граничної похибки вибірки (похибки репрезентативності) та визначення необхідної чисельності вибірки.
Етапи проведення вибіркового дослідження:
1) одним із відомих способів формується вибіркова сукупність, відібрані одиниці сукупності можуть групуватися за певними ознаками;
2) розраховуються узагальнюючі статистичні характеристики вибіркової сукупності: середні величини, структурні показники (частка), які надалі будуть розглядатися як оцінки відповідних характеристик генеральної сукупності;
3) для інтервальної оцінки будується довірчий інтервал, тобто визначаються і записуються межі (від min до max), в яких з певною вірогідністю, очікуються кількісні значення відповідного показника генеральної сукупності.
Основні позначення
| Показники | Позначення | |
| у генеральні сукупності | у вибірковій сукупності | |
| 1. Кількість одиниць сукупності | N | n |
| 2. Середнє значення показника | 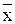
| 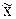
|
| 3. Дисперсія середнього значення | s2 | s2В |
| 4. Питома вага (частка) одиниць сукупності, яким притаманні досліджувані ознаки | р | 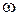
|
| 5. Частка одиниць сукупності, що не мають досліджуваних ознак | q 
| 1- 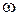
|
| 6. Дисперсія альтернативної ознаки (частки) | р´q | 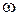 ´(1- ´(1- 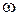 ) )
|
Якщо принцип випадковості відбору не порушувався, то середня похибка вибірки (m) визначається за формулами:
| Вид відбору | Середня помилка вибірки для: | |
| Генеральної середньої | Генеральної частки | |
| Повторний | 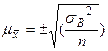
| 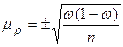
|
| Безповторний | 
| 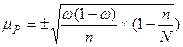
|
З допомогою середньої похибки вибірки, межі довірчого інтервалу для генеральної середньої або частки визначаються з імовірністю лише 0,683. Щоб підвищити імовірність твердження про межі, в які потраплять генеральні характеристики, обчислюють граничну похибку вибірки (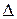 ).
).
 ,
,
де t –коефіцієнт довіри, що підвищує імовірність твердження про потрапляння генеральних узагальнюючих показників до розрахованих довірчих меж.
Щоб добитися довірчої ймовірності = 0,954, середню похибку вибірки подвоюють, тобто t = 2; для довірчої ймовірності = 0,997 довірче число t =3.
Довірчий інтервал записується за формулами:
- для середнього:
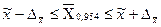
- для частки:
 -
- 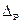
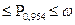 +
+ 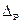
Приклад. З метою вивчення поширеності підприємств громадського харчування за їх величиною, проведено 10 відсоткову безповторну вибірку, яка дала наступні результати (усього в регіоні діє 2120 підприємств):
| Групи підприємств за числом посадочних місць, одиниць | Питома вага, % |
| До 25 | |
| 25 – 50 | |
| Більше 50 | |
| Разом |
Визначте: а) середнє число посадочних місць на одне підприємство; б) з імовірністю 0,954 граничну помилку вибірки та інтервал, в якому знаходиться середнє число місць у підприємств регіону; в) з імовірністю 0,997 довірчі межі для частки підприємств з числом місць до 25.
Розв’язання:
1. Знаходимо середнє число місць для вибраних підприємств:

де хі – число місць, середнє по групі;
fі – число підприємств у групі;
Щоб одержати хі перетворюємо інтервальний ряд розподілу у дискретний (при цьому відкриті інтервали умовно закриваємо за величиною найближчих розташованих поряд інтервалів):
1) 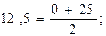 2)
2) 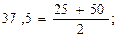 3)
3) 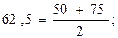

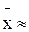 31 місце
31 місце
2. Для розрахунку граничної помилки середньої знаходимо дисперсію:

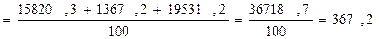

3. Знаходимо граничну помилку для середньої за формулою:
 2,5 (місця).
2,5 (місця).
4. Будуємо довірчий інтервал для середнього числа місць:

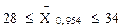
Середнє число місць у підприємствах громадського харчування даного регіону з імовірністю 0,954 знаходиться у межах від 28 до 34 місць.
5. Знаходимо граничну похибку для частки 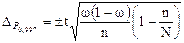

 в % = 9,7 %
в % = 9,7 %
6. Довірчі межі для частки підприємств з числом місць до 25:
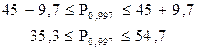
З імовірністю 0,997 можна стверджувати, що частка підприємств, які мають до 25 місць у регіоні знаходиться у межах від 35,3% до 54,7%.
Задачі і завдання для виконання на практичних заняттях
6.1. Середній стаж роботи 50 обстежених працівників підприємства (10%-ний відбір) склав 14,7 року при середньому квадратичному відхиленні 2,1 роки.
Визначте з імовірністю 99,7% граничну помилку вибірки та інтервал, в якому знаходиться середня величина стажу роботи.
6.2. Витрати робочого часу на виробництво однієї деталі у 15 однакових партіях деталей були такими:
| Витрати робочого часу на 1 деталь, люд. год. | Кількість партій |
| 2,8 | |
| 2,9 | |
| 3,0 | |
| 3,4 |
На основі цих даних потрібно обчислити:
а) середні витрати робочого часу на 1 деталь;
б) середнє квадратичне відхилення і дисперсію витрат робочого часу;
в) з імовірністю 0,954 граничну помилку вибірки та інтервал, в якому знаходяться середні витрати робочого часу на 1 деталь.
г) з імовірністю 0,997 граничну помилку вибірки та інтервал, в якому знаходиться частка партій з трудомісткістю 3,4 людино-години.
6.3. Проведено вибіркове обстеження (1%-не) сімей за сукупним доходом на 1 члена і одержані такі дані (дивись таблицю):
Усього в місті проживає 142,8 тис. сімей.
1. Визначте з точністю 99,7% граничну помилку вибірки та інтервал, в якому знаходиться сукупний доход у середньому на одного члена сім’ї.
| Групи сімей за сукупним доходом на одного члена сім’ї, (умовних грошових од.) | Кількість сімей у процентах до підсумку, % | ||
| До 40,0 40,0 – 60,0 60,0 – 80,0 80,0 – 100,0 100,0 – 120,0 120,0 – 140,0 140,0 і більше Разом | |||
2. Обчисліть межі довірчого інтервалу, у якому з імовірністю 0,954 знаходиться частка сімей із доходом на 1 члена сім’ї до 100 грн. на місяць.
6.4. При вибірковому обстеженні трьох відсотків виробів партії готової продукції одержані такі дані про вміст вологи у виробах:
| Відсоток вологи | Кількість виробів |
| До 15,0 15,1 – 17,0 17,1 – 19,0 19,1 – 21,0 21,1 – 23,0 |
Визначте:
а) середній відсоток вологості;
б) середнє квадратичне відхилення;
в) з імовірністю 0,997 граничну помилку вибірки для середньої вологості всієї партії виробів;
г) з імовірністю помилки в 5% межі довірчого інтервалу для частки виробів з вологістю до 19,0 відсотків;
д) скільки виробів із даної партії треба було б обстежити, щоб гранична помилка вибірки при імовірності ствердження 0,997 зменшилася удвоє.






