Студент повинен засвоїти поняття, види і складові елементи рядів динаміки, основні принципи порівнянності даних у цих рядах. Необхідно вивчити порядок обчислення показників для аналізу динаміки: абсолютних відхилень темпів зростання, темпів приросту або зменшення. Вони можуть розраховуватися ланцюговим або базисним способом. Для обчислення ланцюгових показників динаміки рівні ряду динаміки за кожен наступний рік порівнюються з попереднім. Для обчислення базисних показників динаміки рівні динамічного ряду за кожен наступний рік порівнюються, як правило, з початковим (першим) рівнем ряду.
Основні аналітичні і середні показники в рядах динаміки:
1) Абсолютні відхилення знаходять відніманням:
а) ланцюгові ∆л = Уi – Уi -1
б) базисні ∆ б = Уi – У0;
де У –рівень ряду; i – порядковий номер рівня в ряду динаміки.
2) Темпи зростання знаходять діленням:
а) ланцюгові Тл = 
;
б) базисні Тб =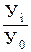 
;
3) Якщо від темпу зростання відняти відносне вираження бази (тобто відняти 1 від коефіцієнта зростання, або 100 від темпу зростання, вираженого у процентах), то одержимо темпи приросту (зменшення):
а) ланцюгові ∆Тл% = Тл% - 100
б) базисні ∆Тб % = Тб % - 100
4) Абсолютне значення 1 % приросту (зменшення) одержують порівнянням ланцюгових абсолютного відхилення і темпу приросту (зменшення) вираженого у процентах:
АЗ1% = 
5) Середній абсолютний рівень ряду динаміки у інтервальних рядах розраховується за формулою простої арифметичної:
у моментних рядах динаміки – за формулою середньої хронологічної:
Із розрахункових (аналітичних) показників динаміки осереднюються лише ланцюгові, базисні показники є накопиченими і осередненню не підлягають.
6) Середнє абсолютне відхилення знаходять за простою арифметичною, як алгебраїчну суму абсолютних ланцюгових відхилень поділену на їх кількість. Тут можна використати і взаємозв’язок: сума ланцюгових відхилень дорівнює останньому базисному абсолютному відхиленню, тому:
,або 
,
де n – це кількість ланцюгових абсолютних відхилень.
Треба пам’ятати, що розрахункових (аналітичних) показників ряду динаміки завжди на 1 менше, ніж вихідних абсолютних рівнів ряду, так як для початкового (першого) вихідного рівня немає бази для порівняння. Тому початковий рівень ряду динаміки часто позначається як нульовий, а кількість розрахункових показників динаміки (n) співпадає з порядковим номером останнього вихідного рівня ряду. Але вихідних рівнів завжди на 1 більше ніж розрахункових, наприклад:
Y0 Y1 Y2 Y3 Y4 Y5 ny=6
D1 D2 D3 D4 D5 nD=5
7) Середній темп зростання визначається за формулою середньої геометричної
,
де Т – ланцюгові темпи зростання, виражені в разах.
Можна використати і взаємозв’язок: добуток ланцюгових темпів зростання дорівнює останньому базисному:
, тоді
Студент повинен засвоїти також порядок розрахунку коефіцієнтів прискорення (уповільнення); випередження (відставання); еластичності.
Приклад: Відомі наступні дані про число працівників фірми (на кінець року, осіб):
| Роки | ||||
| Число працівників, осіб |
Визначте основні аналітичні показники ряду динаміки.
Розв’язання:
1. Визначимо середній рівень динамічного ряду. Ряд моментний, тоді середній рівень знаходимо за середньою хронологічною:
2. Визначимо абсолютні відхилення:
а) ланцюгові: б) базисні
| 4316 – 4191 = + 125 4431 – 4316 = + 115 4541 – 4431 = + 110 | 4316 – 4191 = + 125 4431 – 4191 = + 240 4541 – 4191 = + 350 |
Впевнимося, що сума ланцюгових відхилень дає останнє базисне: +125 + 115 + 110 = 350.
3. Визначимо темпи зростання (у процентах)
а) ланцюгові: б) базисні
| (4316: 4191) х 100 = 103,0 (4431: 4316) х 100 = 102,7 (4541: 4431) х 100 = 102,5 | (4316: 4191) х 100 = 103,0 (4431: 4191) х 100 = 105,7 (4541: 4191) х 100 = 108,4 |
Впевнимося, що добуток ланцюгових темпів зростання, взятих в разах, дає останній базисний темп
1,03 х 1,027 х 1,025 = 1,084
4. Визначимо темпи приросту (у процентах)
а) ланцюгові: б) базисні
| 103,0 – 100 = + 3,0 102,7 – 100 = + 2,7 102,5 – 100 = + 2,5 | 103,0 – 100 = + 3,0 105,7 – 100 = + 5,7 108,4 – 100 = + 8,4 |
Зв’язку між темпами приросту немає
5. Визначимо абсолютне значення одного процента щорічного приросту:
за 2002 рік 
за 2003 рік 
за 2004 рік 
.
Приведені розрахунки оформлюють в таблиці:
| Рік | Число працівників, чол. | Абсолютне відхилення (+;-) | Темп зростання, % | Темп приросту, (зменшення) (+;-), % | Абсолютне значення 1% приросту | |||
| Ланцюгове ∆ л | Базисне ∆б | Ланцю-гове ∆л | Базисне ∆б | Ланцю-гове ∆л | Базисне ∆б | |||
| - | - | - | 100,0 | - | - | - | ||
| +125 | +125 | 103,0 | 103,0 | +3,0 | +3,0 | 41,7 | ||
| +115 | +240 | 102,7 | 105,7 | +2,7 | +5,7 | 42,6 | ||
| +110 | +350 | 102,5 | 108,4 | +2,5 | +8,4 | 44,0 |
6. Визначаємо середнє ланцюгове (щорічне) абсолютне відхилення:
7. Визначаємо середній ланцюговий (щорічний) темп зростання
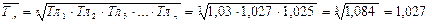або 
8. Визначаємо середній ланцюговий темп приросту (за загальним правилом):
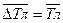- БАЗА 
= 1,027 – 1 = +0,027 (раз)
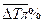= 102,7 – 100 = +2,7 (%)
Таким чином, щорічно число працівників фірми зростало в середньому на 2,7%.
Темпи зростання із року в рік уповільнювалися, про це свідчать значення коефіцієнтів прискорення (уповільнення), які менші від 1.
К1998 до 1997 = 
К1999 до 1998 
Задачі і завдання для виконання на практичних заняттях і домашніх робіт
9.1. Відомі дані про виробничі запаси сировини і матеріалів фірми у порівнянних цінах:
| Вид сировини | Запаси на кінець року, тис. грн. | ||||||
| Цукор | |||||||
| Какао | |||||||
| Шоколадна глазурь | |||||||
| Консерванти | |||||||
| Наповнювачі |
Визначте тип наведених динамічних рядів; розрахуйте середній рівень кожного ряду; обчисліть основні аналітичні показники динамічних рядів (абсолютні відхилення, темпи зростання, темпи приросту або зменшення) за ланцюговим і базисним методами; розрахуйте середні абсолютні відхилення, темпи зростання та середні темпи приросту чи зменшення.
Напишіть короткі висновки.
9.2. Виробництво основних видів продовольчих товарів на душу населення області характеризується такими даними:
| Продукти | Виробництво за рік, кг | |||||||
| М’ясо | 54,5 | 53,2 | 47,8 | 39,3 | 28,4 | 24,3 | 20,1 | 15,6 |
| Молоко | 123,9 | 108,8 | 78,8 | 53,7 | 50,1 | 48,3 | 47,1 | 44,6 |
| Цукор-пісок | 139,8 | 130,9 | 110,2 | 92,0 | 69,9 | 76,5 | 70,2 | 61,3 |
| Олія | 20,6 | 19,3 | 19,8 | 20,1 | 18,6 | 16,4 | 15,9 | 15,2 |
Визначте: 1) тип наведених динамічних рядів і середній рівень кожного ряду; 2) обчисліть абсолютні відхилення, темпи зростання, приросту (чи зниження) за ланцюговим та базисним способом; 3) знайдіть абсолютне значення одного проценту приросту; 4) розрахуйте середні абсолютні відхилення, середні темпи зростання і приросту (чи зменшення). Напишіть висновки.
9.3. Визначте середню чисельність ділових партнерів фірми, за даними про укладені договори:
| Дата | Число договорів на поставку продуктів |
| 1.01.2006 | |
| 1.07.2006 | |
| 1.08.2006 | |
| 1.10.2006 | |
| 1.01.2007 |
9.4. Визначте середньорічний темп зростання і приросту середньодушової суми субсидій, одержуваних громадянами регіону, як адресну допомогу на оплату комунальних послуг, за даними:
| Рік | Середньодушовий розмір субсидій у порівнянному вимірі, грн. |
| 7,6 | |
| 23,4 | |
| 22,6 |
9.5. Кількість безробітних у країні на кінець року становила, тис. чол. 1995 – 12,5; 1999 – 27,8; 2005 – 34,9.
Абсолютний приріст безробіття за 1996–2005 рр. дорівнює:
а) 7,1; б) 22,4; в) 75,2; г) 15,3.
Середньорічний приріст безробіття за 1996–2005 рр. дорівнює:
а) 0,07; б) 2,24; в) 7,52; г) визначити неможливо.
9.6. Прибуток фірми за 2005 рік збільшився на 0,9%, а за 2006 рік ще збільшився на 2,7%. Знайдіть темп зростання і приросту прибутку за два роки.
9.7. За останній рік акціонерний капітал компанії зріс на 20%, абсолютне значення 1% приросту становить 16 тис. грн.
Визначте капітал компанії на початок і кінець року.
9.8. Виробництво прокату у минулому році знизилося на
12,2%, а у поточному на 20%.
Визначте темп зростання виробництва прокату за два роки та середньорічний.
9.9. Виробництво прокату у минулому році зросло в 2,05 рази, у поточному на 60%.
Визначте темп зростання виробництва прокату за два роки та середньорічний.
9.10. За 2004 рік інвестиції фірми становили 106 тис. грн. За 2005 рік обсяг інвестицій збільшився на 16, а за 2006 рік – на 29 тис. грн.
Визначте середньорічний темп приросту інвестицій за два роки.
9.11. Середньорічний абсолютний приріст безробіття в області за 1996–1999 рр. становив 1,2 тис. осіб; за 2000–2002 рр. – 0,99 тис. осіб.
Визначте темп приросту безробіття за увесь період з 1996 по 2002 рр., якщо в 1995 році у області налічувалося 94,5 тис. осіб безробітних.
