Час розглядають як фактор, під дією якого збільшується чи зменшується рівень динамічного ряду:
 ,
,
де t = 0, 1, 2,.... n – значення змінної часу;  – теоретичні рівні ряду, розраховані за трендовим рівнянням.
– теоретичні рівні ряду, розраховані за трендовим рівнянням.
Студент повинен засвоїти способи і прийоми вибору функціонального виду тренду. У індивідуальному завданні для самостійної роботи, як правило, передбачено використання лінійного тренду  = a + bt.
= a + bt.
Параметри трендового рівняння розраховують за методом найменших квадратів. Система нормальних рівнянь має вид:
 na + båt = åУ
na + båt = åУ
aå t+ båt2 = åУt
Якщо число рівнів ряду динаміки не парне, то центральний рівень ряду приймають за базисний. Відлік часу переносять у середину ряду: t cерединне = 0; у минуле йдуть від’ємні, а у майбутнє – додатні ранги, тоді å t = 0,  ,
,  .
.
Етапи аналітичного вирівнювання:
1. Побудова емпіричного ряду динаміки із фактичних рівнів (Уі).
2. Перевірка його на наявність тенденції, наприклад за критерієм Кокса-Стюарта.
3. Вибір функціонального виду тренду.
4. Розрахунок параметрів трендового рівняння: a -?; b -?
Якщо значення змінної часу t позначено порядковими рангами, то
å t = (1 + n)n/2; åУ = У1 + У2 + У3 + …Уn;
å t2 = 1/12 n (n2 – 1) – якщо ранги часу центровані і
å t2 =  - якщо ранги часу порядкові;
- якщо ранги часу порядкові;
åYt = Y1 × t1 + Y2 × t2 + … Yn × tn.
Приклад позначення періодів часу: t1 t2 t3 t4 t5
порядковими рангами tі = 1 2 3 4 5
центрованими рангами tі = -2 -1 0 1 2
5. Перевірка тісноти та істотності зв’язку.
Для перевірки тісноти зв’язку, як правило, застосовують теоретичний коефіцієнт детермінації:
R2 = 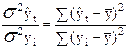 , та
, та
теоретичне кореляційне відношення R =  .
.
Для оцінки істотності зв’язку можна використати таблиці критичних значень коефіцієнта детермінації R2, або розрахувати F – критерій Фішера:
Fрозрах. =  ,
,
де k1 – число ступенів свободи для дисперсії теоретичних значень 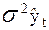 ,
,
k1 = m – 1, де m – число параметрів у трендовому рівнянні (звичайно
m = 2, для параболи m = 3),
k2 – число ступенів свободи для залишкової дисперсії
 , k2 = n – m,
, k2 = n – m,
де n – число рівнів ряду динаміки.
Якщо Fрозрах.> Fтабличне, то зв’язок визнається істотним.
6. Якщо зв’язок варіації Yі зі змінною часу tі визнано за істотний, то тенденцію можна продовжити за межі емпіричного динамічного ряду у майбутнє (екстраполювати тренд). Це робиться з метою прогнозування. При цьому прогнозні значення Yt одержують із рівняння тренду, в якому приймають t = tn + v, де v – період упередження прогнозу.
7. Якість прогнозу оцінюють за відносною помилкою апроксимації, яка не повинна перевищувати 15%, у крайньому випадку допустимим значенням вважається  = 30%
= 30%

8. Довірчі межі прогнозного інтервалу встановлюють з допомогою середньоквадратичної похибки прогнозу.
Студент повинен уміти пояснити значення усіх перерахованих показників.
Приклад. Відомі умовні дані про обсяги експорту із країни:
| Рік (t) | ||||||
| Експорт, (У) млн. дол. | 230,0 | 238,0 | 252,0 | 245,0 | 273,0 | 269,0 |
За допомогою аналітичного вирівнювання визначте експортну можливість країни на 2007 рік, обчисліть критерій Фішера, відносну помилку апроксимації, граничну помилку моделі для рівня істотності a = 0,05. зробіть висновки.
1. Перевіряємо динамічний ряд на наявність тренду за критерієм Кокса-Стюарта.

 230; 238; 252; 245; 273; 269;
230; 238; 252; 245; 273; 269;
І третина ІІІ третина
273 > 230 “+” 2 “+”
269 > 238 “+” 0 “–”
є тенденція до зростання ряду.
2. Позначимо фактор часу “t” і ранжуємо ряд від 1 до n: 1; 2; 3; 4; 5; 6.
3. Побудуємо кореляційне поле

Тенденція може бути апроксимована за прямою:

5. обчислимо параметри а та b із системи рівнянь:
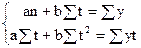
Допоміжна таблиця:
| Час t | Експорт у | t2 | yt | y2 | 
| 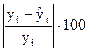
| 
|
| 230,2 | 0,09 | 0,04 | |||||
| 238,6 | 0,25 | 0,36 | |||||
| 246,9 | 2,02 | 26,01 | |||||
| 255,3 | 4,20 | 106,09 | |||||
| 263,7 | 3,41 | 86,49 | |||||
| 272,1 | 1,15 | 9,61 | |||||
| 1507,0 | 11,12 | 228,60 |


–5b = – 41,9
b = 8,38

a = 221,8
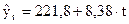
Щорічно оборот з експорту в середньому зростає на 8,38 млн. дол. США. А теоретичні (за рівнянням) обсяги експорту становлять:
 = 221,8 + 8,38 · 1 = 230,2
= 221,8 + 8,38 · 1 = 230,2  = 221,8 + 8,38 · 4 = 255,3
= 221,8 + 8,38 · 4 = 255,3
 = 221,8 + 8,38 · 2 = 238,6
= 221,8 + 8,38 · 2 = 238,6  = 221,8 + 8,38 · 5 = 263,7
= 221,8 + 8,38 · 5 = 263,7
 = 221,8 + 8,38 · 3 = 246,9
= 221,8 + 8,38 · 3 = 246,9  = 221,8 + 8,38 · 6 = 272,1
= 221,8 + 8,38 · 6 = 272,1
5. Для перевірки істотності зв’язку знайдемо теоретичний коефіцієнт детермінації
 ,
,
де  – загальна дисперсія експорту:
– загальна дисперсія експорту: 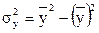
 – залишкова дисперсія експорту:
– залишкова дисперсія експорту: 
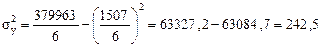


Це означає, що на 84,3% обсяги експорту обумовлені трендом, що склався в динамічному ряді.
F – критерій Фішера.

де n – число років = 6
m – число параметрів лінійного тренду – їх 2 (а; b).

Табличне, критичне значення F знайдемо в стандартній таблиці за значеннями (n – m) та (m – 1):






