Сила варіації (мінливості, коливання) значень ознак кількісно оцінюються з допомогою показників варіації:
1) розмах варіації 
2) Середнє лінійне відхилення:
а) просте (за незгрупованими даними) 
б) зважене (за згрупованими даними) 
3) Середнє квадратичне відхилення (степенева середня другого степеня із індивідуальних відхилень)
а) просте 
б) зважене 
4) Дисперсія Д =  2 , або іншим способом: Д =
2 , або іншим способом: Д =  , де
, де
 та
та 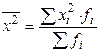
Загальна дисперсія розпадається на міжгрупову і середню із групових дисперсій. Всі види дисперсій широко застосовуються для дисперсійного аналізу аналітичних групувань, оцінки помилок вибіркового обстеження і т.ін. Студент повинен засвоїти порядок обчислення загальної, міжгрупової та середньої із групових дисперсій і знати випадки їх застосування.
5) Для оцінки типовості середньої використовують середньоквадратичний коефіцієнт варіації (V):

Якщо  , то сукупність вважається однорідною, а середня – типовою.
, то сукупність вважається однорідною, а середня – типовою.
Приклад. Дослідження фірм за обсягами їх річної товарної продукції дало наступні результати:
| Групи фірм за обсягом продукції, тис. грн. | Кількість фірм у групі, одиниць |
| До 100 | |
| 100-150 | |
| 150-200 |
Визначте показники варіації продукції. Зробіть висновок про однорідність сукупності і типовість середнього значення продукції для даних фірм.
Розв’язання:
Для розрахунків рекомендується оформити розрахункову (допоміжну) таблицю:
| Групи фірм за обсягом продукції, тис. грн. (інтервали) | Кількість фірм у групі, од. (fі) | Середина інтервалу (продукція) (Хі) | Xifi |
Xi- 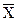
| (Xi-  )2 )2
| (Xi-  )2·fi )2·fi
|
| 50-100 | -44,3 | 1962,5 | 11774,9 | |||
| 100-150 | 5,7 | 32,5 | 877,2 | |||
| 150-200 | 55,7 | 3102,5 | 6205,0 | |||
| Р а з о м | - | - | 18857,1 |
1) Знаходимо середню продукцію 1 фірми:

2) Знаходимо дисперсію


3) Знаходимо середньоквадратичне відхилення

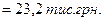
4) Знаходимо коефіцієнт варіації

Так як V<33,3%, то сукупність вважається однорідною, а середня – типовою.
Задачі і завдання для виконання на практичних заняттях і домашніх робіт
5.1. За відомими даними про вік робітників двох молодіжних бригад визначте окремо для кожної бригади модальне число років, медіану, перший та третій квартілі із наведених рядів розподілу.
| вік | Кількість робітників, чол. | |
| Бригада №1 | Бригада №2 | |
| - | ||
| 18,5 | ||
| 19,5 | ||
| 20,5 | ||
| Разом |
5.2. Опитування споживачів про прийнятну для них ціну на новий товар дало наступні результати:
| Ціна товару, грн. | 10-12 | 12-14 | 14-16 |
| Частка споживачів, що признає її прийнятною, % до опитаних |
Визначте: 1) середню прийнятну ціну на даний товар; 2) усі відомі вам показники варіації (розмах варіації, середнє лінійне відхилення, дисперсію, середньоквадратичне відхилення); 3) середньоквадратичний коефіцієнт варіації. Зробіть висновок про однорідність сукупності і типовість середньої.
5.3. Розподіл сімей за рівнем середньодушового грошового доходу характеризується такими даними за місяць:
| Групи сімей за рівнем доходу на 1 чол. у місяць, (умовних грошових од.) | Число сімей | |
| міських | сільських | |
| До 30,0 | 9,2 | 22,8 |
| 30,1 – 60,0 | 18,5 | 38,7 |
| 60,1 – 90,0 | 39,1 | 26,5 |
| 90,1 – 120,0 | 17,0 | 7,9 |
| Більше 120,0 | 16,2 | 4,1 |
Визначте: 1) коефіцієнти варіації рівня середньодушового грошового доходу за окремими категоріями сімей; 2) порівняйте варіацію доходів міських і сільських сімей. Знайдіть моду і медіану розподілу.
5.4. Відомі наступні дані про розподіл фірм за числом працівників:
| Групи фірм за числом працівників, осіб | Кількість фірм |
| До 30 | |
| 30-50 | |
| 50-70 | |
| 70-90 | |
| 90-110 | |
| 110-130 | |
| 130 і більше | |
| Разом |
Обчисліть: 1) середню чисельність працівників; 2) показники варіації (середні лінійне та квадратичне відхилення, дисперсію, коефіцієнт варіації); 3) моду, медіану, квартілі та крайні децилі. Зробіть висновок про однорідність сукупності та типовість середньої.
Тема 6. Вибірковий метод.
З даної теми планується лекція і практичне заняття. Самостійна розрахункова робота виконується вдома за індивідуальними варіантами і надається викладачеві для перевірки.
Питання для розгляду на практичному занятті:
1. Сутність і переваги вибіркового методу.
2. Способи поширення вибіркових даних на генеральну сукупність.
3. Помилки вибіркового спостереження, їх розрахунок і визначення меж довірчих інтервалів.
4. Визначення необхідної чисельності вибірки.
Література: 1; 2; 3; 4; 5; 6; 7; 8; 11.
Термінологічний словник
Сукупність генеральна - це вся сукупність об’єктів, що реально існують, про які потрібно зробити певні висновки, і з яких тим чи іншим способом проводиться відбір одиниць до вибіркової сукупності. Генеральна сукупність може бути обмеженою (кінцевою) або безкінечною.
Сукупність вибіркова – це частина одиниць генеральної сукупності, відібраних із неї у випадковому порядку для проведення вибіркового спостереження.
Принцип випадковості відбору – забезпечення рівних шансів кожній одиниці сукупності бути відібраною і потрапити до вибірки.
Репрезентативність відбору - забезпечення достатньої чисельності вибірки, так щоб у вибірковій сукупності були представлені всі типи явищ, які існують у генеральній сукупності і бажано у тих же співвідношеннях.
Методичні рекомендації до






