Однією із основних задач диференціального числення є знаходження похідної 
заданої функції 
. Різноманітні питання математичного аналізу і його застосувань приводять до оберненої задачі: для даної функції знайти таку функцію 
, похідна якої рівна , тобто 
= .
Відтворення функції за відомою її похідною - одна із основних задач інтегрального числення.
Функція називається первісною для функції , на деякому проміжку Х, якщо для усіх значень х Î Х виконується рівність = .
Якщо - первісна для функції , то й функція 
, де С - довільна стала, також є первісною для функції , оскільки ( )′ = + С ′= + 0 = .
Нехай первісною функції на проміжку Х, крім функції , є функція 
, тобто 
= . Розглянемо різницю - . Обчислимо похідну цієї різниці.
( - )′ = - = - = 0.
Отже, згідно з теоремою Лагранжа - = С. Звідси маємо: = + С.
Таким чином, множина первісних функції на проміжку Х, вичерпується функціями виду + С, де - одна із первісних функції .
Означення. Сукупність усіх первісних функції на проміжку Х називається невизначеним інтегралом функції на цьому проміжку і позначається 
.
Невизначений інтеграл інакше називають інтегралом Ньютона - Лейбніца.
Якщо - одна з первісних функції , то за означенням
= + С.
Знак 
називається знаком невизначеного інтеграла, - підінтегральною функцією, а 
- підінтегральним виразом.
Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.
Основні властивості невизначеного інтеграла
1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції.
( )′ = + С ′= .
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
d ( ) = d = d(x).
3. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної постійної.
= .
4. Сталий множник можна виносити за знак інтеграла, тобто, якщо k = const ¹ 0, то
.
Для доведення цієї властивості досить показати, що права чстина рівності є первісною підінтегральної функції:
.
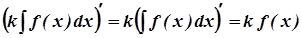5. Невизначений інтеграл від суми (різниці) функцій дорівнює сумі (різниці) невизначених інтегралів від кожної функції, тобто
.
Доведення.
.
Таблиця основних інтегралів
Безпосередньо із означення визначеного інтеграла випливають наступні формули, котрі утворюють таблицю основних інтегралів:
1. 
,
2. 
,
3. 
,
4. 
5. 
,
6. 
,
7. 
,
8. 
,
9. 
,
10. 
,
11. 
,
12. 
,
13. 
,
14. 
Безпосереднє інтегрування
Обчислення інтегралів за допомогою безпосереднього використання таблиці основних інтегралів та їх властивостей називається безпосереднім інтегруванням.
Приклади.
1. 
.
2. 
. 3. 
.
4..
Метод підстановки
В основі методу підстановки (методу заміни змінної) лежить формула диференціювання складеної функції. Якщо F ′(x) = f (x), х Î(a, b), то для довільної диференційованої на проміжку (a, b) функції x = j(t), де j(t) Î(a, b), якщо t Î(a, b) маємо:
(F (j(t)))′ = F ′(x) j′(t) = f (x) j′(t) = f (j(t)) j′(t).
Таким чином,
,
тобто
.
Приклади.
1. Обчислити інтеграл 
.
Розв’язування. Покладемо 
, 
. Тоді
.
2. Обчислити інтеграл 
.
Розв’язування. Покладемо 
. Отже,
.
Інтегрування частинами
Нехай функції 
і 
визначені й диференційовані на деякому проміжку Х. Тоді
.
Звідси маємо
.
Припустимо, що інтеграл 
існує. Тоді
.
Оскільки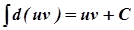 
, то
. (1)
Довільну сталу С включає в себе інтеграл .
Формула (1) називається формулою інтегрування частинами.
За цією формулою обчислюються, зокрема інтеграли виду
1) 
, 
, 
,
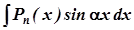де 
- многочлен n -ного степеня відносно х, 
. Тут слід прийняти 
.
2) 
, 
, 
, 
, 
Тут також - многочлен n -ного степеня відносно х. У цих інтегралах 
.
Приклади.
.
.
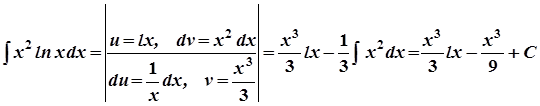ЛЕКЦІЯ 24
34. Подання раціональних дробів у вигляді суми найпростіших дробів.
35. Інтегрування найпростіших раціональних дробів.
1. Подання раціональних дробів у вигляді суми найпростіших дробів
Розглянемо дробово-раціональну функцію 
, де -
многочлен n -го степеня, а 
- многочлен k -го степеня. Якщо n ³ k, то, виконавши ділення, одержимо
,
де r < k. Наприклад,
.
У вищій алгебрі доводиться, що кожний многочлен можна подати у вигляді добутку
, (1)
де А -коефіцієнт при старшому членові многочлена 
, а 
- корені рівняння = 0. Множники 
називаються елементарними. Якщо серед них є однакові, то групуючи їх, одержимо
, (2)
де 
. Числа 
називаються кратностями коренів 
. Серед коренів можуть бути й комплексні. Якщо 
- r -кратний комплексний корінь многочлена з дійсними коефіцієнтами, то цей многочлен має також спряжений з 
r -кратний корінь 
. Отже, якщо формула (2) містить множник 
, де 
, то вона також містить і множник 
. Перемноживши ці множники, одержимо
= 
,
де 
, 
, p, q - дійсні числа.
Ураховуючи всі комплексні корені многочлена , формулу (2) можна записати у вигляді
,
де 
- дійсні числа.
Дріб 
, де r < n називається правильним раціональним дробом.
Теорема. Правильний раціональний дріб , де
можна єдиним чином подати у вигляді суми найпростіших дробів
,
де 
- дійсні числа.
Подання, про яке йдеться у наведеній теоремі, можна виконати методом невизначених коефіцієнтів, котрий розглянемо на наступному прикладі.
Приклад. Розкласти на найпростіші дроби
.
Розв’язування. Згідно з наведеною теоремою маємо:
,
де 
- поки що невідомі числа.
Зведемо праву частину останньої рівності до спільного знаменника.
Два многочлени тотожно рівні між собою тоді й тільки тоді, коли рівні між собою коефіцієнти при однакових степенях х. Тому для визначення коефіцієнтів складемо систему
Розв’язавши цю систему, одержимо:
.
Отже,
.
