Важливе значення у курсі математичного аналізу мають так звані теореми про середнє значення диференціального числення, в яких під знаком похідної знаходиться середнє значення незалежної змінної, котре взагалі нам невідоме. Воно і похідній надає, в деякому розумінні, середнє значення. У зв’язку з цим усі ці теореми називають “теоремами про середнє”.
Теорема Ферма
Теорема. Нехай функція 
визначена на інтервалі 
і в деякій точці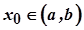 
має найбільше або найменше значення. Тоді, якщо в цій точці існує похідна 
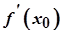, то вона рівна нулю, тобто 
.
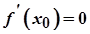Доведення. Нехай для визначеності функція функція в точці 
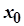приймає найбільше значення, тобто 
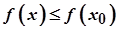для всіх 
.
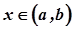За означенням похідної
,
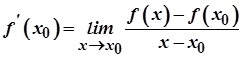причому ця границя не залежить від того, як 
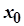буде прямувати до . Якщо 
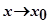і 
, то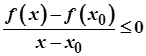 
, а тому
.
Якщо ж 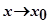і 
, то 
.
Отже,
.
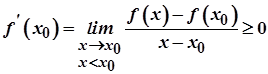Звідси випливає, що .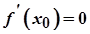
Аналогічно розглядається випадок, коли в точці 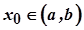функція досягає найменшого значення.
Обертання в нуль похідної в точці 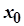, означає, що дотична до графіка функції 
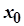в точці з абсцисою паралельна вісі 
(рис. 22).
Зауваження. Теорема Ферма справедлива, коли 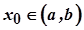, і неправильна, коли замість інтервалу розглядати відрізок 
. Наприклад, функція 
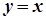на відрізку 
приймає найменше значення в точці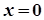 
, а найбільше в точці 
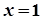. Проте в жодній із цих точок похідна в нуль не обертається.
Теорема Ролля
Теорема. Якщо функція визначена на відрізку і вона
1) неперервна в кожній точці відрізка .
2) диференційована на інтервалі .
3) на кінцях відрізка приймає рівні значення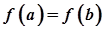 
,
то існує точка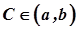 
така, що 
.
Доведення. Оскільки функція неперервна на відрізку , то за другою теоремою Вейєрштрасса існують точки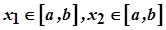 
, в яких функція приймає найменше 
і найбільше 
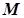значення, тобто 
і 
.
Якщо 
, то функція на відрізку приймає постійне значення, оскільки . Тому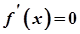 
в будь-якій точці інтервалу .
Якщо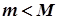 
, то принаймні одне із значень або 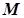функція приймає у деякій точці 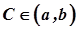, тобто на кінцях відрізка (оскільки ).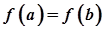
Так як функція диференційована в точці 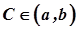, то за теоремою Ферма 
.
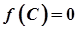Із теореми Ролля випливає, що для функції неперервної на відрізку , диференційованої на інтервалі і такої, що 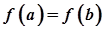, існує точка 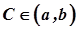така, що дотична до графіка функції у точці 
паралельна вісі (рис. 23).
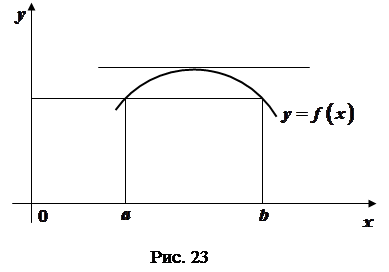
Теорема Лагранжа
Якщо функція визначена на відрізку і вона
1) неперервна в кожній точці відрізка ,
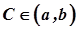2) диференційована на інтервалі , то існує точка така, що
.
Доведення. Розглянемо допоміжну функцію
.
Ця функція визначена на відрізку і задовольняє всім умовам теореми Ролля. Дійсно,
1) оскільки і 
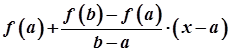неперервні функції на відрізку , то і функція 
також неперервна на .
2) функція диференційована на інтервалі :
.
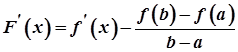3) на кінцях відрізку функція має рівні значення
.
За теоремою Ролля існує точка 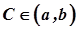така, що 
, тобто
.
Звідси маємо
.
Зауваження. Якщо функція на відрізку задовольняє умовам теореми Лагранжа, то із останньої формули одержуємо
.
Ця формула називається формулою скінчених приростів або формулою Лагранжа. Якщо в цій формулі покласти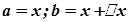 
, то одержимо
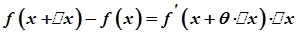, де 
.
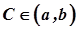Геометричний зміст теореми Лагранжа полягає в наступному. Якщо функція задовольняє умовам теореми Лагранжа, то існує точка така, що дотична до графіка функції у точці паралельна хорді, проведеній через точки 
(рис. 24).
