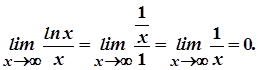1. Якщо функція 
на відрізку 
, має похідну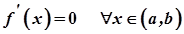 
, то на відрізку стала.
Враховуючи, що похідна від сталої функції дорівнює нулю, що було установлено раніше, і сформульований щойно наслідок. можна сформулювати критерій сталості диференційованої на заданому проміжку функції:
Для того, щоб функція , диференційована на проміжку 
, була сталою, необхідно і достатньо, щоб її похідна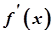 
була рівною нулю в усіх точках цього проміжку.
3) Якщо функції і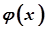 
неперервні на проміжку і при будь-якому 
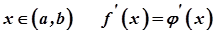, то функція 
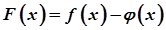є сталою, тобто 
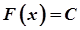, де 
.
Теорема Коші
Теорема. Якщо функції і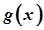 
1) неперервні на відрізку ,
2) диференційовані на інтервалі , і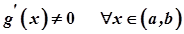 
,
то існує точка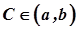 
така, що 
.
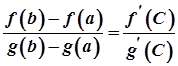Доведення. Побудуємо допоміжну функцію
.
Легко перевірити, що ця функція задовольняє всім умовам теореми Ролля: 
неперервна на , диференційована на і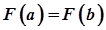 
. Отже, за теоремою Ролля існує точка 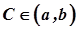така, що 
. Оскільки
,
то
.
Звідси маємо
.
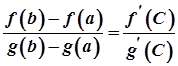Одержана формула називається формулою Коші або узагальненою формулою скінчених приростів.
Зауваження. У формулі Коші 
тому, що за умови 
, згідно з теоремою Ролля існувала б точка 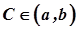така, що 
, що суперечить умові .
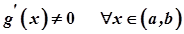ЛЕКЦІЯ 19
22. Розкриття невизначеностей. Правило Лопіталя.
2.Застосування правила Лопіталя при розкритті невизначеностей вигляду 
.
Розкриття невизначеностей. Правило Лопіталя.
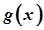Теорема 1 (правило Лопіталя). Нехай функції і визначені в проміжку 
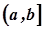і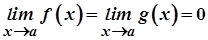 
. Нехай, крім того, в проміжку 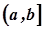існують скінченні похідн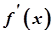і і 
, причому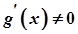 
. Тоді, якщо існує границя 
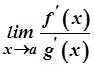, то існує й границя 
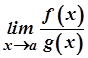, причому
.
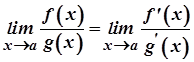Доведення. Доозначимо в точці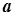 
функції і 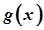, поклавши 
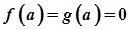. Тоді на відрізку 
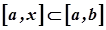функції і 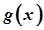задовольняють умовам теореми Коші. Отже,
,
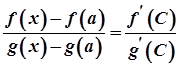де 
. Якщо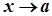 
, то зрозуміло, що й 
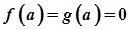. Враховуючи, що і те, що існує границя 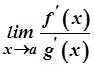, робимо висновок
.
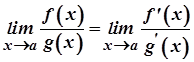Зауваження. Якщо похідні 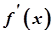і задовольняють умовам, котрі накладаються в наведеній теоремі на функції і 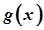, то правило Лопіталя можна застосувати повторно, тобто
.
Теорема 1 справджується й тоді, коли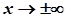 
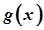. Нехай функції і визначені в проміжку 
, 
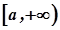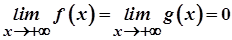, і в проміжку 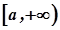існують скінчені похідні 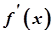та , де 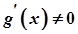. Тоді, якщо існує границя 
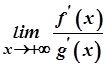, то існує й границя 
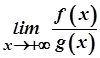, причому
.
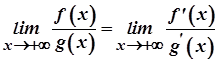Для доведення цього твердження достатньо покласти 
і застосувати теорему 1.
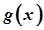Теорема 2 (правило Лопіталя). Нехай функції і визначені в проміжку , 
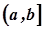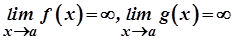і в проміжку 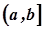існують скінчені похідні 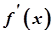та , причому 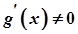. Тоді, якщо існує границя 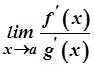, то існує й границя 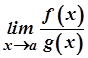, причому
.
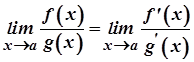Доведення цієї теореми можна прочитати, наприклад, в книзі Г. М. Фихтенгольца “Основы математического анализа”, т. 1. - М.: Наука, 1964. Теорема 2 має місце також, коли .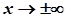
Правило Лопіталя дає можливість розкривати невизначеності типу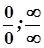 
.
Приклади.
1. 
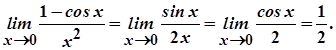
2. 
