Правило Лопіталя можна застосовувати при розкритті невизначеностей вигляду  .
.
Приклади.
1. 
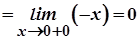 .
.
2. 
 .
.
3.  .
.
4. 

Знайдемо  .
.
Отже,  .
.
5.  .
.
Знайдемо 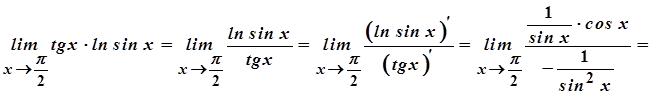
 .
.
Отже, 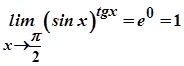 .
.
ЛЕКЦІЯ 20
23. Формула Тейлора для многочлена.
24. Формула Тейлора для довільної функції.
Формула Тейлора для многочлена.
Розглянемо многочлен
 ,
,
де  - дійсні числа. Продиференціюємо многочлен
- дійсні числа. Продиференціюємо многочлен 
 раз.
раз.

Якщо в наведених формулах покласти 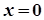 , то одержимо
, то одержимо

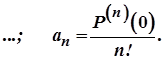
Отже, можна записати
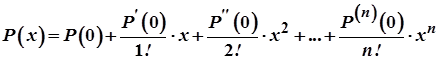 (1)
(1)
Нехай маємо многочлен  за степенями
за степенями  , де
, де 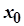 - деяке стале дійсне число, тобто
- деяке стале дійсне число, тобто
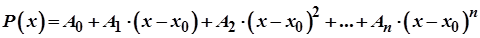 ,
,
де 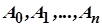 - дійсні числа. Поклавши
- дійсні числа. Поклавши  , матимемо
, матимемо
 .
.
Звідси аналогічно до попереднього, одержимо
 (2)
(2)
Формула (1) є окремим випадком ( ) формули (2). Кожну із цих формул називають формулою Тейлора. Формулу (1) інакше називають формулою Маклорена.
) формули (2). Кожну із цих формул називають формулою Тейлора. Формулу (1) інакше називають формулою Маклорена.
Формула Тейлора для довільної функції
Теорема Тейлора. Нехай функція  в точці
в точці 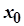 і в деякому її околі має похідні
і в деякому її околі має похідні  - го порядку. Нехай також
- го порядку. Нехай також 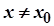 деяка точка, що належить околу, про який йде мова. Тоді існує точка
деяка точка, що належить околу, про який йде мова. Тоді існує точка  , яка лежить між точками
, яка лежить між точками 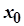 і
і  , така, що
, така, що
 (3)
(3)
Доведення. Позначимо
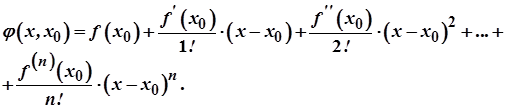
Покладемо

Покажемо, що існує точка  така, що
така, що
 .
.
Зафіксуємо довільну точку  із вказаного околу точки
із вказаного околу точки 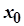 . Для визначеності уважатимемо, що
. Для визначеності уважатимемо, що  . Нехай
. Нехай  - змінна, яка пробігає значення відрізку
- змінна, яка пробігає значення відрізку 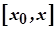 . Складемо допоміжну функцію
. Складемо допоміжну функцію
 .
.
Функція  на відрізку
на відрізку 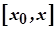 задовольняє всім умовам теореми Ролля:
задовольняє всім умовам теореми Ролля:
1)  неперервна на
неперервна на 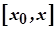 ,
,
2)  диференційована на
диференційована на 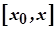 ,
,
(ці властивості функції  випливають із умов, накладених на функцію
випливають із умов, накладених на функцію  )
)
3) на кінцях відрізка 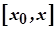 функція
функція  має рівні значення. Дійсно
має рівні значення. Дійсно


Отже, за теоремою Ролля існує точка 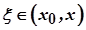 така, що
така, що  . Знайдемо
. Знайдемо  .
.

Оскільки в правій частині одержаної формули знищуються всі члени, за виключенням двох останніх, то
 .
.
Далі маємо:
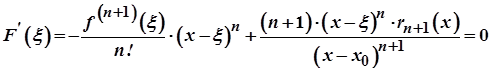 .
.
Звідси одержуємо:
 .
.
Формула (3) називається формулою Тейлора, а одержаний вираз  - залишковим членом у формі Лагранжа.
- залишковим членом у формі Лагранжа.
Оскільки 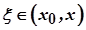 , то
, то  , де
, де  . Тоді
. Тоді
 , де
, де  .
.
Якщо в формулі Тейлора покласти 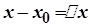 , то тоді
, то тоді

При  маємо формулу Лагранжа
маємо формулу Лагранжа

Якщо функція  в околі точки
в околі точки 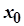 обмежена, то залишковий член
обмежена, то залишковий член  є нескінченно малою вищого порядку порівняно з
є нескінченно малою вищого порядку порівняно з 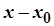 при
при  . Дійсно
. Дійсно
 .
.
Отже, залишковий член  можна подати у формі
можна подати у формі
 при
при  ,
,
яка називається формою Пеано.
Якщо в формулі Тейлора покласти  , то одержимо формулу Маклорена
, то одержимо формулу Маклорена
 .
.
У цій формулі залишковий член у формі Лагранжа має вигляд
 де
де  ,
,
а в формі Пеано
 .
.
Приклади. Записати формулу Маклорена для функції 1)  ; 2)
; 2) 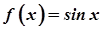 ; 3)
; 3) 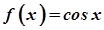 .
.
Розв'язування.
1)  . Оскільки
. Оскільки  , то
, то 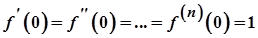 . Отже,
. Отже,
 .
.
2) 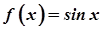 . Так як
. Так як 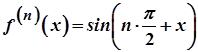 , то
, то
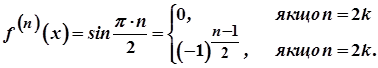
Звідси маємо
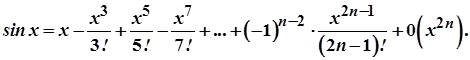
3) 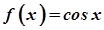 .
.  ;
;
 ;
;

ЛЕКЦІЯ 21
25. Ознака монотонності функції.
26. Екстремальні точки.
27. Необхідні й достатні умови існування екстремуми функції.
4. Знаходження найбільшого й найменшого значення функції на відрізку.






