Нехай функція  визначена на інтервалі
визначена на інтервалі  і в кожній точці цього інтервалу має скінчену похідну. Тоді в кожній точці
і в кожній точці цього інтервалу має скінчену похідну. Тоді в кожній точці  графіка цієї функції можна провести дотичну, не паралельну осі
графіка цієї функції можна провести дотичну, не паралельну осі  . Крива, яка є графіком цієї функції, називається гладкою.
. Крива, яка є графіком цієї функції, називається гладкою.
Якщо крива, яка є графіком функції  , розміщена не нижче будь-якої дотичної на інтервалі
, розміщена не нижче будь-якої дотичної на інтервалі  , то вона називається вгнутою догори або просто вгнутою на цьому інтервалі. Іноді її ще називають опуклою вниз (рис. 25).
, то вона називається вгнутою догори або просто вгнутою на цьому інтервалі. Іноді її ще називають опуклою вниз (рис. 25).
Якщо крива, яка є графіком функції  , розміщена не вище будь-якої дотичної на інтервалі
, розміщена не вище будь-якої дотичної на інтервалі  , то вона називається вгнутою донизу або просто опуклою на цьому інтервалі. Таку криву ще називають опуклою вгору (рис. 26).
, то вона називається вгнутою донизу або просто опуклою на цьому інтервалі. Таку криву ще називають опуклою вгору (рис. 26).
 |
Точка  називається точкою перегину гладкої кривої
називається точкою перегину гладкої кривої  , якщо існує
, якщо існує  -окіл точки
-окіл точки  такий, що в інтервалах
такий, що в інтервалах  і
і 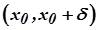 крива
крива  має опуклість різних напрямків (рис. 27).
має опуклість різних напрямків (рис. 27).
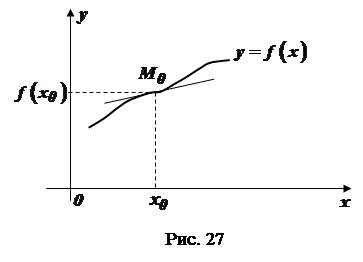
У цьому випадку графік функції  в інтервалах
в інтервалах  і
і 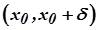 лежить по різні боки від дотичної, проведеної в точці
лежить по різні боки від дотичної, проведеної в точці  .
.
Теорема. Нехай функція  визначена на інтервалі
визначена на інтервалі  і в кожній точці цього інтервалу має похідні до другого порядку включно. Тоді, якщо
і в кожній точці цього інтервалу має похідні до другого порядку включно. Тоді, якщо  у всіх точках
у всіх точках 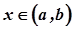 , то графік функції
, то графік функції  на інтервалі
на інтервалі  вгнутий (опуклий вниз), якщо ж
вгнутий (опуклий вниз), якщо ж  у всіх точках
у всіх точках 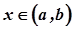 , то графік функції
, то графік функції  на інтервалі
на інтервалі  опуклий (опуклий вгору).
опуклий (опуклий вгору).
Доведення.  в інтервалах
в інтервалах  і
і 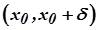 лежить по різні боки від дотичної, проведеної в точці
лежить по різні боки від дотичної, проведеної в точці  .
.
Нехай 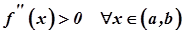 . Виберемо точку
. Виберемо точку 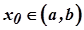 і покажемо, що графік функції
і покажемо, що графік функції  лежить не нижче дотичної, яка проходить через точку
лежить не нижче дотичної, яка проходить через точку  . Щоб відрізняти ординату графіка функції і ординату дотичної, останню будемо позначати буквою
. Щоб відрізняти ординату графіка функції і ординату дотичної, останню будемо позначати буквою  . Запишемо рівняння дотичної в точці
. Запишемо рівняння дотичної в точці  :
:
 (1)
(1)
Оскільки функція  має похідні до другого порядку включно, то згідно формули Тейлора (при
має похідні до другого порядку включно, то згідно формули Тейлора (при 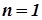 ) маємо:
) маємо:
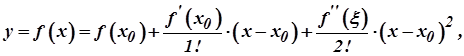 (2)
(2)
де  . Віднімемо від рівності (2) рівність (1)
. Віднімемо від рівності (2) рівність (1)
 .
.
Оскільки  , то
, то  , тобто
, тобто  . Отже, графік функції
. Отже, графік функції  у будь-якій, відмінній від
у будь-якій, відмінній від  , точці
, точці 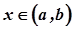 лежить вище дотичної, проведеної до нього в точці з абсцисою
лежить вище дотичної, проведеної до нього в точці з абсцисою  .
.
Аналогічно доводиться теорема для випадку  .
.
Установимо необхідну умову існування точки перегину графіка функції  . Нехай функція
. Нехай функція  визначена і має неперервні похідні до другого порядку включно на інтервалі
визначена і має неперервні похідні до другого порядку включно на інтервалі  . Тоді. Якщо в кожній точці
. Тоді. Якщо в кожній точці 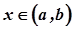
 , то графік функції
, то графік функції  на інтервалі
на інтервалі  вгнутий (опуклий вниз). Якщо
вгнутий (опуклий вниз). Якщо  ,
, 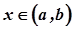 , - то графік опуклий (опуклий вгору).
, - то графік опуклий (опуклий вгору).
Отже, якщо на інтервалі 
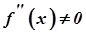 , то графік функції
, то графік функції  точок перегину на цьому інтервалі не має. Таким чином, точка
точок перегину на цьому інтервалі не має. Таким чином, точка  , де
, де 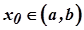 може бути точкою перегину графіка функції
може бути точкою перегину графіка функції  лише в тому випадку, коли
лише в тому випадку, коли  .
.
Отже, умова  є необхідною, для того, щоб точка
є необхідною, для того, щоб точка  була точкою перегину графіка функції
була точкою перегину графіка функції  .
.
 Покажемо, що не всяка точка
Покажемо, що не всяка точка  за умови
за умови  є точкою перегину. Розглянемо такий приклад: Нехай
є точкою перегину. Розглянемо такий приклад: Нехай  . Тоді
. Тоді  при
при  . Але точка
. Але точка  не є точкою перегину графіка функції
не є точкою перегину графіка функції  (рис. 28).
(рис. 28).
Установимо достатню умову існування точки перегину графіка функції  . Нехай точка
. Нехай точка  така, що
така, що  й існує таке
й існує таке  , що в інтервалах
, що в інтервалах  і
і 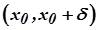 друга похідна
друга похідна  має різні знаки. Тоді точка
має різні знаки. Тоді точка  є точкою перегину. Дійсно, за вказаних умов у інтервалах
є точкою перегину. Дійсно, за вказаних умов у інтервалах  і
і 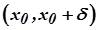 крива
крива  має опуклість різних напрямків. Отже, точка
має опуклість різних напрямків. Отже, точка  є точкою перегину цієї кривої.
є точкою перегину цієї кривої.
Зауваження. Точка  є точкою перегину графіка функції
є точкою перегину графіка функції  і в тому випадку, коли в точці
і в тому випадку, коли в точці  існує дотична до графіка функції
існує дотична до графіка функції  , друга похідна в самій точці
, друга похідна в самій точці  не існує, але існує в деякому
не існує, але існує в деякому  -околі точки
-околі точки  , причому в інтервалах
, причому в інтервалах  і
і 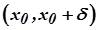 має різні знаки.
має різні знаки.
Це установлюється аналогічно попередньому.
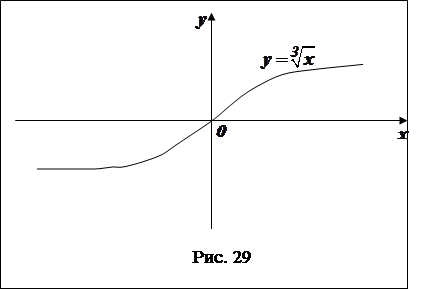 Приклад. Нехай
Приклад. Нехай  . Ця функція в точці
. Ця функція в точці  має нескінченну похідну першого порядку й дотична до її графіка в точці
має нескінченну похідну першого порядку й дотична до її графіка в точці  співпадає з віссю
співпадає з віссю  . Друга похідна в точці
. Друга похідна в точці  не існує. Графік функції
не існує. Графік функції  в точці
в точці  має перегин, оскільки справа і зліва від точки
має перегин, оскільки справа і зліва від точки  друга похідна
друга похідна 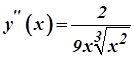 має різні знаки (рис. 29).
має різні знаки (рис. 29).
Асимптоти графіка функції
Пряма 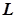 називається асимптотою кривої
називається асимптотою кривої  , якщо відстань від точки
, якщо відстань від точки 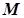 кривої до прямої
кривої до прямої 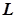 при віддаленні точки
при віддаленні точки 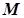 у нескінченність прямує до нуля.
у нескінченність прямує до нуля.
Із наведеного означення випливає, що асимптоти можуть існувати лише у тих кривих, які мають як завгодно віддалені точки, тобто у “нескінчених” кривих.
Надалі розрізнятимемо похилі і вертикальні асимптоти. До похилих асимптот належать також і горизонтальні асимптоти.
Теорема. Якщо функція  визначена на нескінченості і існують границі
визначена на нескінченості і існують границі
 (1)
(1)
то пряма  є похилою асимптотою кривої
є похилою асимптотою кривої  при
при  .
.
Аналогічно, якщо існують границі
 (2)
(2)
то пряма  є похилою асимптотою кривої
є похилою асимптотою кривої  при
при  .
.
Доведення. Розглянемо випадок  . Оскільки за умовою існують границі (1), то
. Оскільки за умовою існують границі (1), то  . Число
. Число 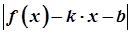 дорівнює довжині відрізка від точки
дорівнює довжині відрізка від точки 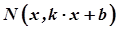 прямої
прямої  до точки
до точки  графіка функції
графіка функції  (рис. 30).
(рис. 30).


Відстань  від точки
від точки  до прямої
до прямої  рівна
рівна  , де
, де  - кут, який утворює пряма
- кут, який утворює пряма  з додатним напрямом вісі
з додатним напрямом вісі  (
( , оскільки мова йде про похилі асимптоти). Отже,
, оскільки мова йде про похилі асимптоти). Отже,  =
= 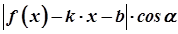 . Тоді
. Тоді
 .
.
Випадок, коли  доводиться аналогічно.
доводиться аналогічно.
Якщо  , то пряма
, то пряма 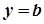 є горизонтальною асимптотою графіка функції
є горизонтальною асимптотою графіка функції  при
при  . Те ж стосується і випадку
. Те ж стосується і випадку  .
.
Зауваження. Якщо не існує границя  , то не існує і границя
, то не існує і границя  . Отже, у цьому випадку графік функції
. Отже, у цьому випадку графік функції  при
при  асимптот не має. Якщо границя
асимптот не має. Якщо границя  існує і рівна
існує і рівна 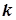 , а границя
, а границя  не існує, то у цьому випадку графік функції
не існує, то у цьому випадку графік функції  також асимптот не має.
також асимптот не має.
Із означення асимптоти кривої  випливає, що пряма
випливає, що пряма  є вертикальною асимптотою, якщо принаймні одна з границь
є вертикальною асимптотою, якщо принаймні одна з границь  або
або  рівна
рівна  або
або  .
.






