Теорема. Нехай 
- критична точка функції 
, неперервна в точці і має похідну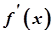 
в усіх точках околу 
за виключенням, можливо самої точки . Тоді
1) якщо 
і 
, то точка є точкою максимуму функції .
2) якщо 
і 
, то точка є точкою мінімуму функції .
3) Якщо 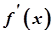в околі має один і той же знак, то не є точкою екстремуму функції .
Доведення. 1). Нехай і . Звідси за ознаками монотонності функції маємо: якщо 
і 
. Отже, для будь-якого 
із околу виконується нерівність 
, тобто точка є точкою максимуму функції .
Доведення пунктів 2), 3) аналогічні.
Із сказаного випливає правилодослідження функції на екстремум. Щоб дослідити функцію на екстремум треба:
1. Знайти область визначення функції.
2. Знайти 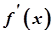- першу похідну функції .
3. Розв’язати рівняння 
та визначити ті значення 
, при яких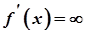 
або 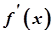не існує. Нехай після виконання цих дій одержано точки 
, які знаходяться в інтервалі 
області визначення функції .
4. У кожному з інтервалів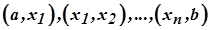 
взяти довільну точку і визначити в ній знак першої похідної. Який знак матиме похідна у вибраній точці, такий же знак вона матиме й у відповідному інтервалі.
5. Розглянути знак 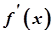у сусідніх інтервалах, переходячи послідовно зліва направо від першого інтервалу до останнього. Якщо при цьому знаки 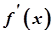у двох сусідніх інтервалах різні. То в критичній точці є екстремум: максимум, якщо знак змінюється з “+” на “-“, мінімум, якщо знак змінюється з “-“ на “+”. Якщо ж у двох сусідніх інтервалах знак першої похідної не змінюється. То екстремуму у відповідній критичній точці немає.
Приклад. Дослідити наекстремум функцію
.
Розв’язування.
1. Функція визначена в інтервалі 
.
2. 
.
3. Розв’язками рівняння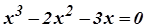 
є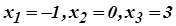 
.
4. В інтервалі 
, функція спадає; в інтервалі 
, функція зростає; інтервалі 
, функція спадає; в інтервалі 
, функція зростає.
5. Точки 
є точками мінімуму, а точка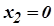 
є точкою максимуму даної функції.
6. 
.
Для знаходження екстремумів функції можна застосовувати другу похідну 
. Це випливає із наступної теореми.
Теорема. Нехай - стаціонарна точка функції і в цій точці існує похідна другого порядку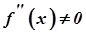 
. Тоді, якщо 
, то точка є точкою мінімуму функції , а якщо 
, то – максимуму.
Доведення. Згідно з умовою теореми 
. Нехай . Тоді похідна 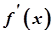в точці є зростаючою функцією, а тому існує окіл точки такий, що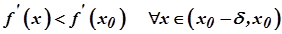 
і 
. Оскільки , то і , тобто при переході через точку похідна 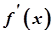змінює свій знак з “-“ на “+”. Отже, точка є точкою мінімуму функції .
Випадок, коли 
досліджується аналогічно.
Скориставшись формулою Тейлора, можна довести наступну теорему.
Теорема. Якщо в стаціонарній точці функції перша відмінна від нуля похідна 
є похідною парного порядку, то точка є точкою екстремуму функції : точкою мінімуму, якщо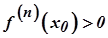 
і точкою максимуму, якщо 
. Якщо ж перша відмінна від нуля похідна є похідною непарного порядку, то точка не є точкою екстремуму функції .
4. Знаходження найбільшого й найменшого значення функції на відрізку
Для знаходження найбільшого й найменшого значення функції , неперервної на відрізку 
, потрібно знайти всі її локальні екстремуми на цьому відрізку та її значення на кінцях відрізка, тобто 
. Потім з одержаних значень вибрати найменше й найбільше.
ЛЕКЦІЯ 22
1. Опуклість та вгнутість кривої. Точки перегину.
2. Асимптоти графіка функції.
3. Загальна схема дослідження функцій і побудови їх графіків.
