Похідна сталої функції. Похідна функції 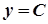 , де
, де  при
при  виражається формулою
виражається формулою  .
.
Доведення.
 .
.
Похідна степеневої функції  . Область визначення
. Область визначення 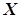 цієї функції залежить від
цієї функції залежить від 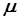 . Візьмемо довільну відмінну від нуля внутрішню точку
. Візьмемо довільну відмінну від нуля внутрішню точку  області визначення
області визначення 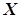 . Тоді
. Тоді


 .
.
Зауваження. Якщо  , то легко безпосередньо одержати значення похідної при
, то легко безпосередньо одержати значення похідної при 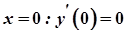 . Отже, для будь-якої точки
. Отже, для будь-якої точки  , де
, де 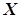 - область визначення функції
- область визначення функції  , маємо:
, маємо:  .
.
Приклади. 


Похідна показникової функції  .
.


Приклади. 

Похідна логарифмічної функції  .
.

 Зокрема, якщо
Зокрема, якщо  , то
, то  .
.
Похідні тригонометричних функцій.
Нехай  . Тоді
. Тоді
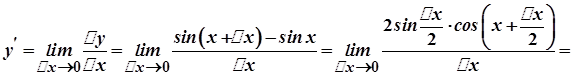

Аналогічно доводиться, що функція  має похідну
має похідну  .
.
Якщо  , то
, то



Аналогічно доводиться, що функція
 має похідну
має похідну  .
.
Похідна оберненої функції.
Теорема. Нехай функція  задовольняє всі умови теореми про існування оберненої функції і в точці
задовольняє всі умови теореми про існування оберненої функції і в точці 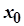 має похідну
має похідну  . Тоді обернена до неї функція
. Тоді обернена до неї функція  у точці
у точці 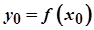 має похідну і
має похідну і
 .
.
Доведення. Надамо значенню  деякий приріст
деякий приріст  . Тоді функція
. Тоді функція  одержить відповідний приріст
одержить відповідний приріст  . Оскільки
. Оскільки  , то за однозначністю функції
, то за однозначністю функції  ,
,  . Отже,
. Отже,  .
.
Якщо  , то за неперервністю функції
, то за неперервністю функції 
 . Звідси маємо
. Звідси маємо
 .
.
Похідні обернених тригонометричних функцій. Нехай маємо функцію  . За означенням функції
. За означенням функції 
 .
.
Згідно теореми про похідну оберненої функції
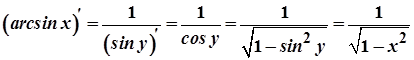 .
.
Зауваження. Тут враховано, що при  виконуються співвідношення
виконуються співвідношення  , тобто
, тобто  . Отже,
. Отже,  , а тому
, а тому  . Точки
. Точки  не розглядаються, так як
не розглядаються, так як 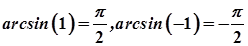 і
і  .
.
Аналогічно одержуються похідні інших обернених тригонометричних функцій:

ЛЕКЦІЯ 17
13. Диференціал функції.
14. Похідні вищих порядків.
15. Формула Лейбніца для п -ної похідної добутку двох функцій.
16. Диференціали вищих порядків.
Диференціал функції
Нехай функція  диференційована в точці
диференційована в точці 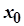 . Тоді її приріст у цій точці можна подати у вигляді
. Тоді її приріст у цій точці можна подати у вигляді
 ,
,
де  при
при  . Отже, доданок
. Отже, доданок  є головною частиною приросту функції, яка лінійно залежить від
є головною частиною приросту функції, яка лінійно залежить від  .
.
Диференціалом функції  в точці
в точці 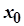 називається головна частина приросту функції в цій точці, яка лінійно залежить від
називається головна частина приросту функції в цій точці, яка лінійно залежить від  .
.
Диференціал функції позначається так:
 .
.
Враховуючи, що  , маємо
, маємо
 .
.
Диференціалом незалежної змінної  називається її приріст:
називається її приріст:  .
.
Отже,
 .
.
Із останньої формули випливає, що похідну 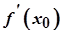 можна обчислити як відношення диференціалів:
можна обчислити як відношення диференціалів:
 .
.
Диференціал функції має наступний геометричний зміст. Нехай точка 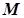 (рис. 21) на графіку функції
(рис. 21) на графіку функції  має координати
має координати  , де
, де 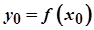 .
.
 |

 |
Пряма  - дотична до графіка функції в точці
- дотична до графіка функції в точці 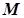 . Тоді приріст
. Тоді приріст  в точці
в точці 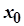 , який відповідає приросту
, який відповідає приросту  аргументу, рівний величині відрізка
аргументу, рівний величині відрізка 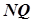 . Оскільки
. Оскільки  і
і  , то, враховуючи, що
, то, враховуючи, що  , маємо: диференціал
, маємо: диференціал  функції
функції  в точці
в точці 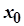 дорівнює приросту ординати дотичної, проведеної до графіка функції
дорівнює приросту ординати дотичної, проведеної до графіка функції  в точці з абсцисою
в точці з абсцисою 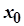 , тобто дорівнює величині відрізка
, тобто дорівнює величині відрізка 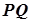 .
.
Оскільки диференціал  функції
функції  є головною частиною її приросту, то це дає можливість застосувати диференціал функції в наближених обчисленнях: із наближеної рівності
є головною частиною її приросту, то це дає можливість застосувати диференціал функції в наближених обчисленнях: із наближеної рівності 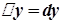 , тобто
, тобто
 .
.
Отже
 (1)
(1)
Приклад. Знайти наближено  .
.
Розв'язування. Розглянемо функцію  . Покладемо
. Покладемо 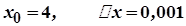 . Тоді
. Тоді  . Далі маємо
. Далі маємо 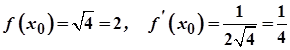 .
.
Отже,  .
.
Якщо функції  диференційовані, то мають місце наступні формули:
диференційовані, то мають місце наступні формули:
 ,
,
 ,
,
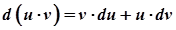 ,
,
 .
.
Нехай тепер маємо складену функцію  , де
, де  диференційовані функції в точках
диференційовані функції в точках 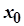 і
і  . Тоді
. Тоді
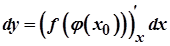 .
.
Так як
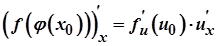 ,
,
то
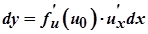 .
.
Оскільки  , то маємо
, то маємо  .
.
Таким чином, якщо функція складена, то форма диференціалу не змінює свого виду. Цю властивість називають інваріантністю форми диференціалу.






