Разовьем последний из подходов к построению метода Эйлера. Очевидно, применение к интегральному равенству (13) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (1)-(2).
Так, если в (13) использовать простейшую квадратурную формулу правых прямоугольников, придем к методу
(14)
Этот метод называют неявным (или обратным) методом Эйлера, поскольку для вычисления неизвестного значения 
по известному значению 
требуется решать уравнение, в общем случае нелинейное.
Применение к интегралу в (13) простейшей квадратурной формулы трапеций приводит тоже к неявному методу
(15)
который будем называть методом трапеций. Квадратурная формула трапеций на порядок точнее формул левых и правых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (15) по сравнению с явным и с неявным методами Эйлера (8) и (14), т.е. метод трапеций (15) — это метод второго порядка.
Некоторый интерес представляет совместное применение явного метода Эйлера и неявного метода трапеций.
По форме равенство (15) представляет собой скалярную задачу о неподвижной точке относительно неизвестного значения уi+1. Поэтому, если в правую часть (15) подставить хорошее начальное приближение 
, подсчитываемое по формуле (14), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный метод
i =0,1,..., n, (16)
который называют методом Хойна.
Ясно, что можно достичь большей точности, если, исходя из того же начального приближения
сделать не одну, а несколько итераций по методу трапеций:
(17)
Такой вариант совместного применения метода Эйлера и метода трапеций называют усовершенствованным методом Эйлера-Коши с итерационной обработкой. Делать много итераций по формуле (17) не рекомендуется (обычно их выполняют не более трех-четырех). Совпадение определенного числа разрядов в полученных числах 
говорит о точности, с которой решено методом простых итераций уравнение (15) относительно уi+1, а вовсе не о том, что с такой точностью найдено значение у(хi+1).
Чтобы получить следующую модификацию метода Эйлера,
проинтегрируем уравнение (1) по отрезку 
Имеем
откуда следует равенство
(18)
Применяя к последнему интегралу одноточечную квадратурную формулу средних прямоугольников и заменяя значения y(xi-1) и y(xi) известными приближенными значениями уi-1 и уi соответственно, из (18) выводим формулу для подсчета приближенного значения y(xi+1)
(19)
которую будем называть уточненный методом Эйлера.
Как известно, квадратурная формула прямоугольников (средней точки) имеет тот же порядок точности, что и квадратурная формула трапеций, так что уточненный метод Эйлера (19) тоже является методом второго порядка. Подтверждением этого факта может служить вывод метода (19) на разностной основе. Применив к равенству (11) формулу симметричной аппроксимации y'(xi) второго порядка точности, получим
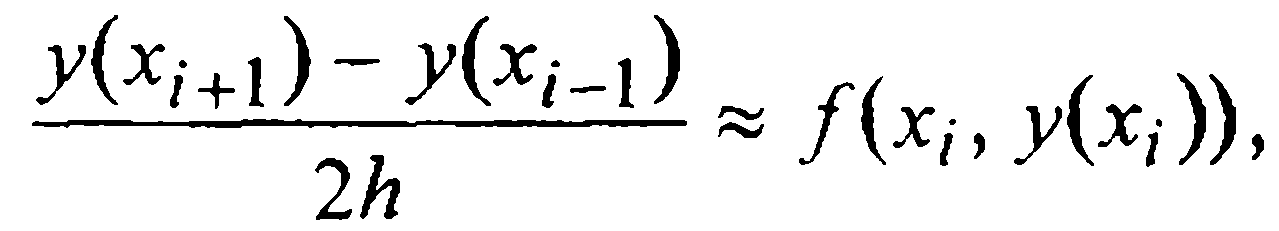
откуда после приближенной замены 
следует(19).
Обратим внимание на одно принципиальное отличие метода (19) от всех других рассмотренных до этого момента методов: метод (19) является двухшаговым. Здесь для вычисления значения уi+1 привлекаются два предыдущих значения уi и уi-1. Двухшаговость накладывает определенные ограничения, по крайней мере, на начало численного процесса: значение 
не может быть найдено непосредственно этим методом с тем же шагом h. Поэтому недостающую вторую начальную для процесса (19) точку приходится получать другим путем, например, явным методом Эйлера, а чтобы не сделать сразу большой ошибки, применяя на старте метод более низкого порядка точности, рекомендуется осуществлять постепенное вхождение в процесс (19). Так, «разгон» можно выполнить по формулам
(20)
а далее уже переключаться на счет по формуле (19).
Пример 1. Рассмотрим простое линейное уравнение 
с начальным условием y(0)=1.
На этой задаче легко проследить за вычислениями, реализующими различные выведенные выше методы. Знание ее точного решения 
позволяет провести сравнение результатов приближенных вычислений по разным формулам с истинным решением и проверить, насколько соответствуют представления о точности тех или иных методов тому, что наблюдается в данном, наверное, далеко не самом типичном частном случае.
Сначала сделаем несколько последовательных приближений по методу Пикара. Его итерационная формула (5) для данной начальной задачи имеет вид
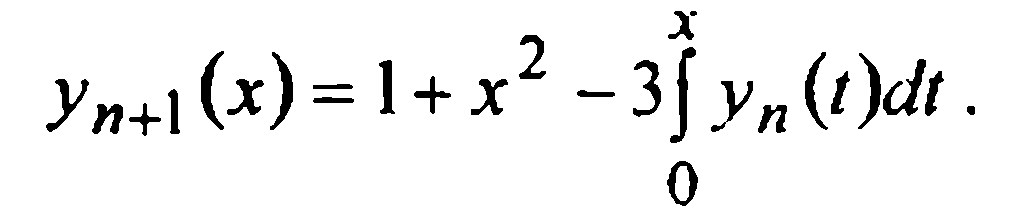
Подставляя сюда у0 =1 при п = 0,1, 2 последовательно получаем:
Эти результаты удобно сравнить с точным решением, если в последнем разложить в ряд по степеням х фигурирующую там функцию e-3x. Тогда получим представление решения в виде ряда
с которым, как видим, хорошо согласуются приближения y1, y2, y3, определяемые методом Пикара.
Теперь проведем подсчет приближенных значений решения у(х) данной задачи в точке х =0.2 численным методом Эйлера и его модификациями, принимая h = 0.1 (т.е. за два шага). Результаты этих вычислении и фактические ошибки, найденные сравнением с точным значением y(0.2) = 0.581881..., отражены в следующей таблице.
| Метод | 
| 
| 
|
| Эйлера (8) | 0.7 | 0.51 | ≈0.07 |
| Неявный Эйлера (14) | ≈0.7846 | ≈0.6343 | ≈-0.05 |
| Трапеций (15) | ≈0.7478 | ≈0.5788 | ≈0.003 |
| Хойна(16) | 0.755 | ≈0.5895 | ≈-0.008 |
| Уточненный Эйлера (19)-(20) | 0.755 | 0.587 | ≈-0.005 |
Исправленный метод Эйлера
Пусть найдено приближенное значение 
решения у = у(х) задачи (1)-(2) и требуется вычислить 
где 
Запишем разложение решения по формуле Тейлора р-го порядка, принимая за базовую точку xi (т.е. по степеням х-хi) и положим в этом разложении x= xi+1. Имеем
(21)
Если ограничится двумя слагаемыми в правой части разложения (21), то, получим обычный метод Эйлера (8). Посмотрим, что дает учитывание третьего слагаемого.
При р = 2 из (21) следует равенство
(22)
Значение первой производной в точке xi в силу связи (1), приближенно известно:
(23)
Дифференцируя (1), по формуле полной производной
находим приближенное значение второй производной:
(24)
Подставляя приближенные выражения 
) в равенство (22), получаем следующую формулу для вычисления 
при i=0, 1, …, n:
(25)
Определяемый ею метод будем называть исправленным методом Эйлера.
Так как при i=0 формулы (23) и (24) точны, а y0 =y (x0), согласно начальному условию (2), то на первом шаге вычислений по формуле (25) будет совершаться ошибка, связанная только с усечением ряда Тейлора. Следовательно, локальная ошибка или, иначе, шаговая погрешность метода (25) составляет величину o(h3), а это означает, что исправленный метод Эйлера относится к методам второго порядка.
