Любой метод из семейства методов Рунге-Кутты второго порядка (30) реализуют по следующей схеме. На каждом шаге, т.е. при каждом i=0, 1, 2,..., вычисляют значения функции
а затем находят шаговую поправку
прибавление которой к результату предыдущего шага дает приближенное значение решения у(х) в точке xi+1 = xi + h:
Метод такой структуры называют двухэтапным по количеству вычислений значений функции — правой части уравнения (1) — на одном шаге.
Анализ устройства методов Рунге-Кутты второго порядка позволяет представить, в какой форме следует конструировать явный метод Рунге-Кутты произвольного порядка. По аналогии с предыдущим для семейства методов Рунге-Кутты p-го порядка используется запись, состоящая из следующей совокупности формул:
(32)
где к = 2, 3, …, р (для р -этапного метода). Многочисленные параметры сk, ак, bkj, фигурирующие в формулах (32), подбираются так, чтобы получаемое методом (32) значение уi+1 совпадало со значением разложения y(xi+1) по формуле Тейлора с погрешностью O(hp+1) (без учета погрешностей, совершаемых напредыдущих шагах).
Наиболее употребительным частным случаем семейства методов(32) является следующий метод Рунге-Кутты четвертого порядка относящийся к четырехэтапным и имеющий вид:
(33)
Не пытаясь воспроизвести выкладки, приводящие от общей записи семейства (32) при р=4 к конкретному методу (33), дадим геометрическое толкование последнего.
Обратив внимание на то, что шаговая поправка Δуi, есть средневзвешенная величина поправок 
каждого этапа (с весовыми коэффициентами 1/6, 2/6, 2/6, 1/6 соответственно), проанализируем, как получаются эти поправки этапов. На первом этапе создается приращение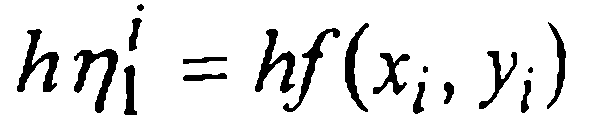 
соответствующее шаговой поправке Эйлера, — это
очевидно. На рис 2 ему отвечает отрезок ВС вертикали
х=xi+1 (точка В получена ортогональным проектированием
точки А на эту вертикаль).
Рис. 2. Геометрическая иллюстрация одного шага методов Рунге-Кутта четвертого порядка
Так как точка М, благодаря свойству средней линии треугольника (см. ΔАВС), имеет ординату 
определяет значение f(M), служащее (согласно связи у =f(x, у) и геометрическому смыслу производной) тангенсом угла А в новом треугольнике с противолежащим этому углу катетом 
Далее, аналогично, подсчитав 
на вертикали x=xi+1 откладываем следующую промежуточную (этапную) поправку 
Вычислив величину f(E)=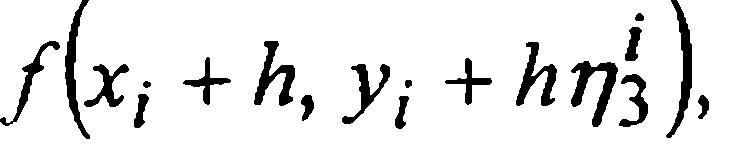 
являющуюся значением тангенса угла А во вновь получаемом ΔABG, имеем поправку 
последнего этапа. Итоговая шаговая поправка 
есть продукт усреднения с указанными коэффициентами четырех этапных поправок — длин отрезков ВС, BD, BE и BG. Точка Н будет стартовой для следующего, i+1-го, шага метода (33).
Заметим, что если первый этап, как уже упоминалось, соответствует применению явного метода Эйлера, то четвертый — неявного, а второй и третий — уточненного методов Эйлера. Последний имеет более высокий порядок точности, отсюда и больший вес отвечающих ему значений этапных поправок.
