Численное дифференцирование применяется в тех случаях, когда: функция f(x) задана таблично и, следовательно, методы дифференциального исчисления неприменимы; аналитическое выражение f(x) столь сложно, что вычисления производной представляют значительны трудности.
В основе численного дифференцирования лежит следующий прием: исходная функция f(x) заменяется на рассматриваемом отрезке [a,b] интерполяционным полиномом Pn(x) и считается, что f'(x) и P'n(x) примерно равны, т.е. f’(x)=P'n(x),.(a < x < b).
Рассматривается следующая задача: дана таблица функции, требуется построить таблицу ее производной с тем же шагом.
Всегда, когда это возможно, для численного дифференцирования используется интерполяционный многочлен с равноотстоящими узлами, так как это значительно упрощает формулы численного дифференцирования. При равноотстоящих узлах в начале строится интерполяционный полином Ньютона, а затем он дифференцируется.
Если f(x) задана таблицей с неравноотстоящими узлами, то вначале строится интерполяционный полином Лагранжа, а затем он дифференцируется.
Будем изучать численное дифференцирование, основанное на первой интерполяционной формуле Ньютона. Из-за больших погрешностей численное дифференцирование практически используется для вычисления производных не выше второго порядка. Обычно при численном дифференцировании интерполяционный полином Ньютона строится не по всем узлам таблицы, а по трем-пяти узлам, близлежащим к точке, в которой требуется вычислить производную. Если требуется вычислить производную во всех узлах, то вначале полином Ньютона строится по первым 3-5 узлам и в них вычисляется производная, потом полином Ньютона строится по следующим 3-5 узлам и в них вычисляется производная и т. д. до тех пор, пока не будет просчитана вся таблица.
Если по узлам x0, xb x2, x3, x4 построить первый интерполяционный полином Ньютона и его продифференцировать с учетом

то получим приближенное выражение для  в виде:
в виде:
 (1)
(1)
Вторая производная f"(x) в результате дифференцирования формулы (1) с учетом равенства

имеет следующее приближенное выражение:
 (2)
(2)
Если требуется вычислить f'(x) в узлах x0, x1, …, xn, то в формулу (1) необходимо поочередно поставить q=0, q=1, q=2, q=3, q=4 соответственно.
В случае выбора узлов xj, xj+1, …, xj+4 вместо узлов x0, x1,...,x4 в формулах (1), (2) следует заменить конечные разности y0 на конечные yj, которые берутся из строчки с номером j таблицы конечных разностей. Если требуется найти производные функции f(x) в основных табличных точка xj то каждое табличное значение считается за начальное и тогда xj=x0, q=0, а формулы (1), (2) будут соответственно для всех f'(x) и f'' (x) иметь вид:
 (1')
(1')
 (2')
(2')
Если интерполяционный полином строится не по пяти, а по четырем или трем узлам, то в формулах (1), (1'), (2), (2') отбрасываются соответственно одно или два последних слагаемых.
Чтобы вычислить значение производной в точке, соответствующей концу таблицы, следует воспользоваться формулой, полученной дифференцированием второй интерполяционной формулы Ньютона, т.е. формулой

Метод неопределенных коэффициентов
Аналогичные формулы можно получить и для случая произвольного расположения узлов. Использование многочлена Лагранжа в этом случае приводит к вычислению громоздких выражении, поэтому удобнее применять метод неопределенных коэффициентов. Он заключается в следующем. Искомое выражение для производной k-го порядка в некоторой точке х=хi представляется в виде линейной комбинации заданных значений функции в узлах х0, x1,..хn:
 (3)
(3)
Предполагается, что эта формула имеет место для многочленов y=1, y=x-xi, у=(х-xi)n. Подставляя последовательно эти выражения в (3), получаем систему n+1 линейных алгебраических уравнений для определения неизвестных коэффициентов с0, с1, …, сn.
Пример. Найти выражение для производной ух в случае четырех равноотстоящих узлов (n = 3).
Равенство (3) запишется в виде
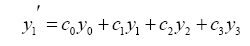 (4)
(4)
Используем следующие многочлены:
 (5)
(5)
Вычислим их производные:
 (6)
(6)
Подставляем последовательно соотношения (5) и (6) соответственно в правую и левую части (4) при х=х1:

Получаем окончательно систему уравнений в виде
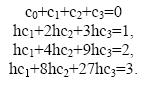
Решая эту систему получаем

Подставляя эти значения в равенство (4), находим выражение для производной:

Задания: выполнить задание 1 и 2 ИДЗ№3.






