Все формулы численного интегрирования дают результат с некоторой погрешностью. Здесь заметим, что уменьшение погрешности расчета является одной из важнейших задач численных методов.
В предыдущем параграфе рассматривались различные квадратурные формулы для равномерного расположения узлов в интервале интегрирования [a, b]. Оказывается, при фиксированном количестве узлов можно добиться значительного уменьшения погрешности вычисления определенного интеграла, если отказаться от их равномерного расположения.
Для нахождения оптимального расположения узлов (которое обеспечивает уменьшение погрешности численного интегрирования) прежде всего сведем интервал интегрирования общего вида [a, b] к стандартному интервалу [-1, 1] с помощью линейной замены переменной интегрирования:
x = (а + b) / 2 + t (b - а) / 2. (25)
Исходный интеграл приобретет вид:
 (26)
(26)
где t - новая переменная интегрирования.
В соответствии с общей квадратурной формулой запишем:
 (27)
(27)
Нашей целью является выбор таких п узлов ti внутри интервала интегрирования [-1, 1] и таких п коэффициентов Ai (i = 1, п), чтобы формула (27) была точной для всех полиномов максимально большой степени. Мы имеем возможность варьировать 2n величин ti и Ai (i=1, …, п), следовательно, эта максимальная степень полинома равна N = 2n - 1.
Далее требуется доказать следующую лемму.
Лемма. Для достижения поставленной цели необходимо и достаточно, чтобы формула (27) выполнялась точно для следующих 2n подынтегральных функций 
Доказательство.
По условиям леммы выполняются следующие равенства для степенных функций f(t) = tk (k = 0, 1, …, 2п- 1):
 (28)
(28)
Как было принято выше, подынтегральную функцию f(t) представим в виде полинома степени 2п - 1:
 (29)
(29)
где Ck - коэффициенты полинома.
Проведем интегрирование полинома (29) по интервалу [-1, 1], используя условие (28) и изменяя порядок суммирования:
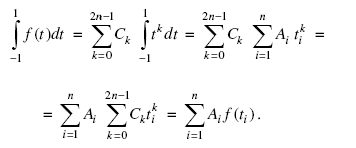 (30)
(30)
Последнее равенство обусловлено определением (29).
Мы получили, что равенство (27) является точным для полинома вида (29), при этом в ходе преобразований мы воспользовались условиями (28).
Лемма доказана.
Эта лемма обеспечивает справедливость следующего важного утверждения. Пусть нам удастся найти такие числа ti и Ai (i = 1, …, n), обращающие формулу (27) в точную, используя в качестве подынтегральных степенные функции вида tk (k = 0, 1,..., 2n - 1). Тогда эти найденные числа ti и Ai обеспечат точность формулы (27) и для любой подынтегральной функции, которая представляется в виде полинома степени 2n - 1.
Теперь в уравнениях (28) проинтегрируем аналитически левые части:
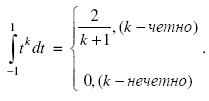 (31)
(31)
Сравнение (31) с правыми частями уравнений (28) дает нам систему 2n уравнений для 2n искомых неизвестных ti, Ai (i = 1,..., n):
 (32)
(32)
Система является нелинейной относительно неизвестных ti, Ai (i = 1,…, n). Для ее решения целесообразно воспользоваться свойствами полиномов Лежандра. Краткие сведения о полиномах Лежандра приведены в приложении 1.
Выберем подынтегральные функции f(x) в виде:
 (33)
(33)
где Pn (t) - полином Лежандра степени n.
Это значит, что все n функций (33) являются полиномами степени ≤ 2n-1. Для таких подынтегральных функций, согласно доказанному выше, формула (27) является точной и коэффициенты Ai (i = 1,…, n) удовлетворяют системе (32).
Применим квадратурную формулу (27) для функций (33):
 (34)
(34)
В силу свойства ортогональности полиномов Лежандра левые части всех уравнений (34) равны нулю. Следовательно, и правые части (34) будут равны нулю
 (35)
(35)
при произвольных значениях Ai, если положить Pn (ti) = 0.
Таким образом, оказывается, что в качестве узлов ti следует взять точки нулей полиномов Лежандра степени n. Точки нулей полиномов Лежандра различных степеней рассчитаны с большой точностью и сведены в специальные таблицы. Характерным свойством узлов ti и коэффициентов Ai в данном методе является симметрия их значений относительно центра таблицы t = 0.
Если числа ti известны, то система (32) становится линейной относительно величин Ai. Для ее решения можно применить любой из описанных методов. Численные значения узлов ti и коэффициентов Ai с точностью до восьми знаков для различных n приведены в таблице приложения 2.
Вычислив значения узлов ti и коэффициентов Ai для выбранного n, можно вернуться к исходной переменной интегрирования x и записать квадратурную формулу Гаусса в следующем виде:
 (36)
(36)
где
 (37)
(37)
Точность интегрирования методом Гаусса резко возрастает с увеличением числа узлов в интервале интегрирования [a, b]. Теоретические оценки и расчеты показывают, что для интервалов небольшой величины обычно достаточная точность обеспечивается при n = 8. Соответствующая таблица узлов ti и коэффициентов Ai приведена в приложении 2.
Если диапазон интегрирования [a, b] имеет значительную ширину, его можно разбить на несколько равных поддиапазонов и провести процедуру вычисления интеграла методом Гаусса для каждого поддиапазона отдельно. Интеграл по j-му поддиапазону с границами [aj, bj ] с помощью линейного преобразования (37) представляется в виде суммы, аналогичной (36):
 (38)
(38)
где 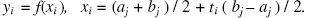
Искомое значение определенного интеграла по полному диапазону [a, b] вычисляется как сумме интегралов (38) по всем поддиапазонам.
Задания: выполнить задание 3 ИДЗ№3.






