Занятие № 14. Численное интегрирование. Квадратурные формулы Ньютона-Котеса

Задача численного интегрирования. Квадратурные формулы прямоугольников

Пусть требуется найти значение I интеграла Римана 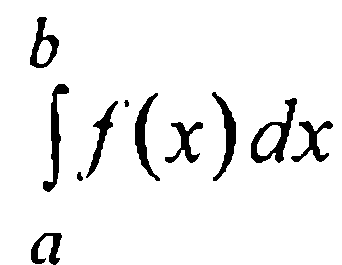для некоторой заданной на отрезке [а, b] функции f(x). Хорошо известно, что для функций, допускающих на промежутке [а, b] конечное число точек разрыва первого рода, такое значение существует, единственно и может быть фор­мально получено по определению:

(1)

где 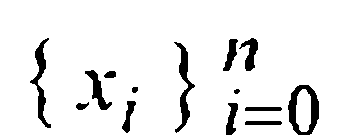— произвольная упорядоченная система точек от­резка [а, b] такая, что

а ξ_i — произвольная точка элементарного промежутка [х_i-1,_ х_i].

В математическом анализе обосновывается аналитический способ нахождения значения I с помощью знаменитой формулы Ньютона-Лейбница

I = F(b)-F(a), (2)

где F(x) — некоторая первообразная для данной функции f(x).

К сожалению, применение этого весьма привлекательного под­хода к вычислению I наталкивается на несколько серьезных препятствий. Самое главное из них — это несуществование пер­вообразной среди элементарных функций для большинства эле­ментарных функций f(x); например, таким способом не удается вычислить

Если первообразная F(x) для заданной функции f(x) все же найдена, то вычисление двух ее значений F(a) и F(b) может оказаться более трудоемким, чем вычисление существенно большего количества значений f(x).

Поскольку в общем случае значения функций находятся лишь приближенно, использование точной формулы (2) приводит к приближенному результату, который может быть более эффективно получен с помощью какой-либо специ­альной приближенной формулы на основе значений подынте­гральной функции f(x). Такие специальные приближенные формулы для вычисления определенных интегралов называют квадратурными формулами (механическими квадратурами) или формулами численного интегрирования. Первый из этих терминов можно связать с геометрическим смыслом определенного интеграла: вычисление при f(х)> 0 равносильно построению квадрата, равновеликого криволинейной трапеции с основанием [а,b] и «крышей» f(x).

Простые квадратурные формулы можно вывести непосред­ственно из определения интеграла, т.е. из представления (1). Зафиксировав там некоторое п≥ 1, будем иметь

(3)

Это приближенное равенство назовем общей формулой прямо­угольников (площадь криволинейной трапеции приближенно за­меняется площадью ступенчатой фигуры, составленной из прямоугольников, основаниями которых служат отрезки[х_i-1, x_i], а высотами — ординаты f(ξ_i), рис. 1).

Рис. 1. Геометрическая интерпретация общей формулы прямоугольников (.3)

 

Чтобы из общей формулы (3) получить конструктивное правило приближенного вычисления интеграла, воспользуемся свободой расположения точек х,, разбивающих промежуток ин­тегрирования [а, b] на элементарные отрезки [x_i-1, x_i], и свобо­дой выбора точек ξ_i на этих отрезках.

Условимся в дальнейшем пользоваться равно­мерным разбиением отрезка [а, b] на п частей точками х_i с шагом 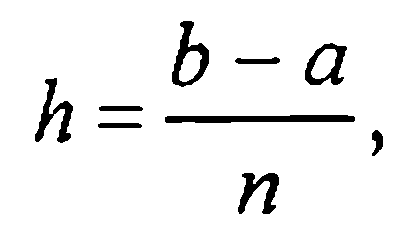полагая

(4)

При таком разбиении формула (3) приобретает вид

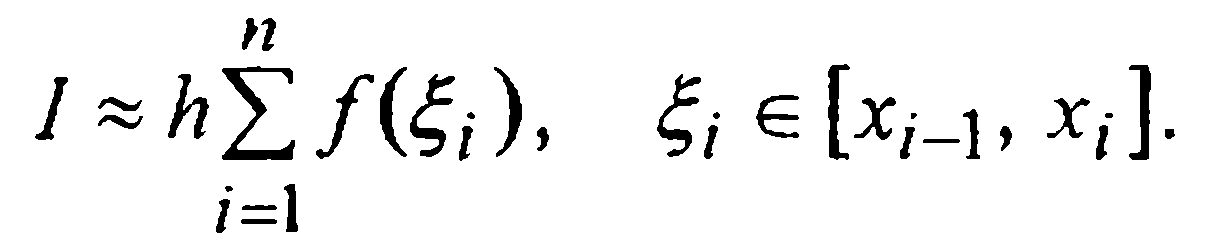(5)

Теперь дело за фиксированием точек ξ_i на элементарных отрез­ах [x_i-1, x_i]. Рассмотрим три случая.

1) Положим ξ_i = x_i-1. Тогда из (5) получаем

(6)

2) Пусть в (5) ξ_i = x_i. Тогда имеем

(7)

Формулы (6) и (7) называются квадратурными формулами левых и правых прямоугольников соответственно. Совер­шенно очевидно (рис. 2), что дают двусторонние приближения к значению I интеграла от монотонной функции.

Рис..2. Геометрическое оценивание интеграла от монотонной функции с помощью:

Можно рассчитывать на большую точность получения зна­чения интеграла, если взять точку ξ_i посередине между точками x_i-1 и x_i. Отсюда приходим к следующему случаю.

3) Фиксируем В ре­зультате имеем квадратурную формулу средних прямоугольни­ков или, иначе, формулу средней точки

(8)

Учитывая априорно большую точность формулы (8) по срав­нению с формулами (6) и (7) при том же объёме и характе­ре вычислений, эту симметричную формулу будем впредь назы­вать просто формулой прямоугольников.

Полученные из определения интеграла квадратурные пра­вила (6)—(8) не содержат в себе сведений, позволяющих сказать, каким нужно взять число п элементарных промежутков [x_i-1, x_i] или, иначе, каким должен быть шаг h разбиения (4) отрезка интегрирования [а, b ], чтобы гарантированно найти зна­чение I интеграла с наперед заданной точностью ε. Ответ на этот вопрос дает формула остаточного члена (гло­бальной погрешности) квадратурной формулы прямоугольни­ков:

(9)

Как видно из формулы (9), при увеличении числа п элементарных отрезков, на которые разбивается промежуток ин­тегрирования [а, b), ошибка численного интегрирования по фор­муле средней точки (8) убывает пропорционально квадрату шага h. Погрешность численного ин­тегрирования непрерывно дифференцируемой функции по фор­мулам левых и правых прямоугольников (6), (.7) убывает лишь по линейному закону.

 

Семейство квадратурных формул Ньютона-Котеса

Подстановка в интеграл 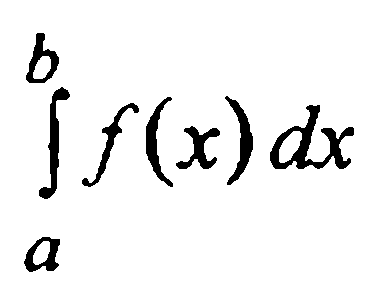вместо функции f(x) её интерполяционного многочлена Лагранжа той или иной степе­ни п приводит к семейству квадратурных формул, называемых формулами Ньютона-Котеса.

Функция f(x ) может быть единственным образом представлена в виде

где — интерполяционный многочлен Лагранжа, — остаточный член, Если система узлов интерполирования 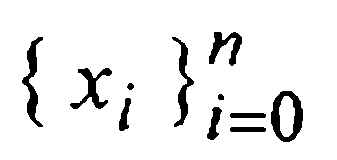совпадает с точками разбиения (4) отрезка [а, b] с шагом h, то замена переменной x=x₀+qh трансформирует многочлен Лагранжа к виду

(10)

Для того, чтобы использовать такое выражение L_n(x) вместо f(х) в нужно изменить границы интегрирования (значению х=а соответствует значение q= 0,а х=b — значе­ние q = п) и учесть, что dx=hdq. Таким образом, получаем

Это равенство, переписанное в виде

(11)

и есть квадратурная формула Ньютона-Котеса, где

(12)

— коэффициенты Котеса.

На самом деле, формулы (11)-(12) определяют се­мейство квадратурных формул. Параметром этого семейства является число п — степень интерполяционного многочлена, ко­торым заменяется подынтегральная функция.

Для практического применения целесообразно рассмотреть некоторые частные случаи.

Пусть n = 1. Это значит, что диапазон интегрирования [a, b] содержит только два узла: x₀ = a и x₁ = b.

Вычислим коэффициенты Котеса для этого случая. Подставляя в (12) n = 1 и i = 0, 1 получим:

(13)

Подстановка коэффициентов (13) в (12) дает квадратурную формулу Ньютона-Котеса первого порядка:

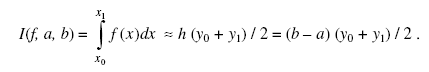(14)

В данном случае величина шага h равна длине всего диапазона интегрирования [a, b].

При таком приближении подынтегральная функция f (x) заменяется линейной (полиномом Лагранжа 1-й степени). Графически значение определенного интеграла I(f, a, b) изображается площадью криволинейной трапеции, ограниченной сверху (или снизу) графиком функции f (x) (см. пример на рис. 3).

Рис.3. К выводу формулы трапеций.

Сплошная линия - график интегрируемой функции f (x),

штрихпунктирная - график линейного приближения интегрируемой функции на интервале [x₀, х₁].

Крестиками заполнена область R, площадь которой равна погрешности квадратурной формулы (14).

 

Приближенное значение интеграла, выраженное квадратурной суммой (14), равно площади обычной трапеции с той же высотой h. Площадь криволинейного сектора дает погрешность R вычисления определенного интеграла с помощью квадратурной формулы (14).

Когда данный способ вычисления определенного интеграла используют на практике, то обычно диапазон интегрирования [a, b] разбивают на N одинаковых поддиапазонов шириной

h = (b - a) /N (15)

и к каждому из них применяют формулу (14). Тогда искомый интеграл представится суммой, каждый член которой будет содержать общий множитель (15). Каждое значение интегрируемой функции y_k (k = 0, 1, …, N) в эту сумму будет входить дважды, кроме двух крайних y₀ и y_N. В результате интеграл I(f, a, b) выразится следующей суммой:

(16)

Последняя формула называется формулой трапеций.

Теперь пусть n=2. Это значит, что диапазон интегрирования [a, b] содержит три узла: х₀=a, x₁=(a+b)/2, x₂=b. В данном случае шаг интегрирования равен половине диапазона интегрирования h=(b-a)/ 2

Коэффициенты Котеса в данном случае получаются вычислением интегралов (11) с подстановкой n = 2 для i = 0, 1, 2:

(7)

Искомый интеграл представится в виде:

(18)
где (b - a) = 2h.

Формула (18) была получена заменой подынтегральной функции f(x) на квадратичную, проходящую через заданные точки (x_i, y_i), i = 0, 1, 2. Полученное значение искомого интеграла графически изображается площадью под параболой (см. рис. 4).

Рис. 4. К выводу формулы Симпсона.

Жирная сплошная линия - график интегрируемой функции f (x),

штриховая - график квадратичного приближения L₂(x) интегрируемой функции на интервале [x₀, x₂]. Заштрихованная область R выражает погрешность квадратурной формулы (18).

Видно, что на интервале [x₀, x₁] квадратичное приближение дает заниженный результат, на интервале [x₁, x₂] - завышенный.

На практике весь диапазон интегрирования [a, b] обычно предварительно разбивается на четное число N = 2M равных интервалов, которые попарно объединяются в M поддиапазонов. Каждый поддиапазон содержит три узла: два крайних и один внутренний. К каждому из M поддиапазонов применяется формула (18), т.е. каждой тройке узлов соответствует своя интерполирующая парабола. Параболы стыкуются в совпадающих крайних узлах отдельных поддиапазонов. Номера всех таких узлов четные от i = 2 до i = 2 M - 2, поэтому при суммировании выражений (18) по поддиапазонам следует учесть, что слагаемые с этими номерами встретятся дважды.

В результате суммирования с учетом значений коэффициентов Котеса (17) получается рабочая формула

(19)

где для краткости введены обозначения следующих сумм:

(20)

Заметим, что сумма S_o содержит M слагаемых, а сумма S_e состоит из M-1 слагаемых. Шаг интегрирования равен h=(b - a)/(2M)=(b - a)/N.

Формула (19) называется квадратурной формулой Симпсона.

При n = 3 аналогичным путем получается квадратурная формула с тремя узлами на интервале интегрирования:

(21)

где h = (b - a) / 3.

При решении прикладных задач диапазон интегрирования [a, b] предварительно разбивается на равные поддиапазоны, число которых кратно трем (N = 3M), и к каждому из поддиапазонов применяется формула (20). Тогда получится рабочая формула вида:

(22)

Шаг интегрирования равен h=(b-a)/(3M) = (b-a)/N, а отдельные суммы выражены следующими формулами:

(23)

Сумма (22) называется квадратурной формулой Ньютона или формулой «трех восьмых». В практике квадратурная формула Ньютона употребляется гораздо реже, чем формулы Симпсона и трапеций.

Задания: выполнить задание 3 ИДЗ№3.