Цель - ознакомить студентов с многошаговыми методами Адамса решения задачи Коши для обыкновенных дифференциальных уравнений.
Будем строить численные методы решения начальной задачи
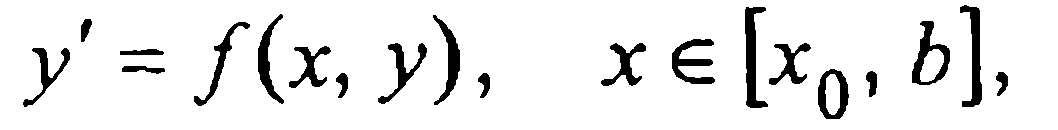(1)
(2)
Будем считать, что уже найдено несколько приближенных значений 
(j = 0,1,..., i) решения у=у(х) задачи (1)-(2) на равномерной сетке xj=x0 + jh, и нужно получить правило для вычисления очередного значения 
Для вывода таких правил используем интегро-интерполяционный подход. А именно, проинтегрировав левую и правую части уравнения (1) по промежутку [xi, xi+1], в полученном равенстве
(3)
под интеграл вместо функции f(x,у(х)) подставим интерполирующий ее многочлен 
Хотя выражение функции f(x,y(x)) как функции одной переменной х, вообще говоря, неизвестно, ее дискретные приближенные значения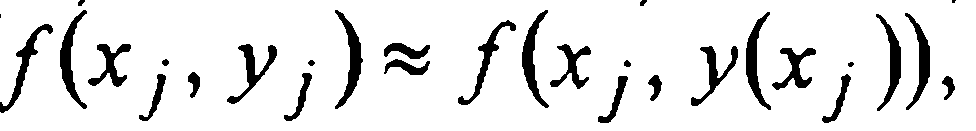 
обозначаемые в дальнейшем для краткости fj, при j=1, 2,..., j можно считать известными. В таком случае, дополняя эти известные значения пока что неизвестным значением 
можно построить таблицу конечных разностей (табл. 1), служащую основой для образования
интерполяционных многочленов к-й степени для интерполирования назад из точек 
Таблица 1
Таблица конечных разностей для построения конечноразностных формул Адамса
При интерполировании назад из узла хi, по второй интерполяционной формуле Ньютона имеем
(4)
(см.конечные разности, подчеркнутые в табл. 1 сплошной линией), а из узла xi+1 по той же формуле получаем многочлен
(5)
(использующий разности, подчеркнутые пунктиром).
Подстановка многочленов 
в равенство (3) приводит к формулам для вычисления очередного значения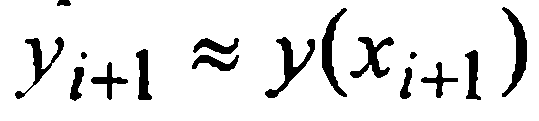 
вида
(6)
и
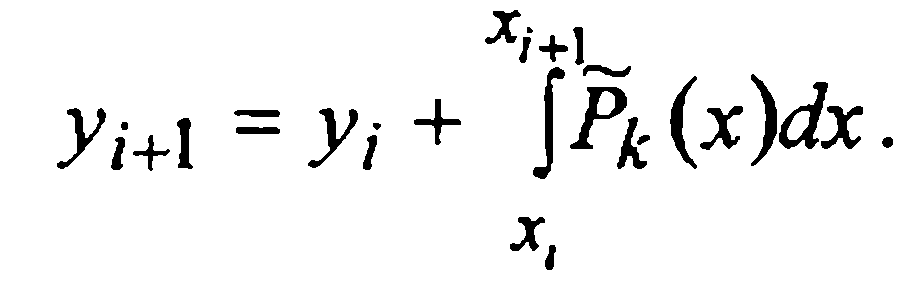(7)
В результате применения к интегралам в (6) и (7) формулы Ньютона-Лейбница получается два семейства методов (с параметром k∈N0), называемых многошаговыми методами Адамса. Рассмотрим по отдельности каждое из этих семейств.
Экстраполяционные методы Адамса-Башфорта. Чтобы подставить в (6) многочлен (4), зависящий от переменной 
сделаем в интеграле 
замену переменной 
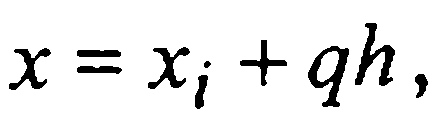всоответствии с которой
Тогда формула (6) может быть переписана в виде
(8)
где
(9)
Таким образом, на основе (8) получается следующая конечно-разностная формула, определяющая экстраполяционный метод Адамса-Башфорта:
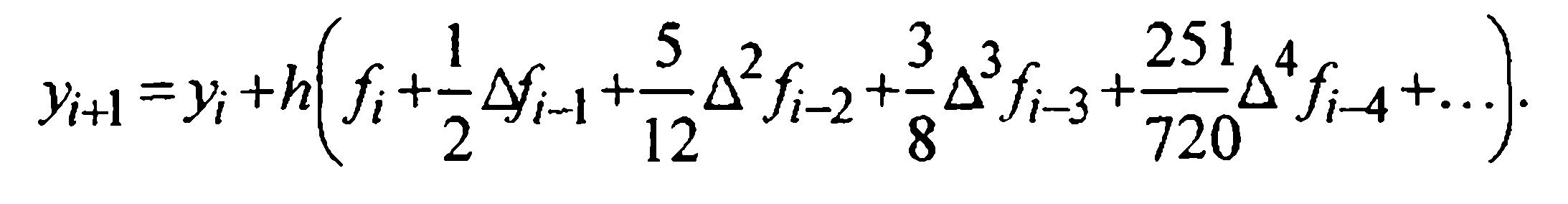(10)
Посмотрим, что представляют собой наиболее простые частные случаи метода Адамса-Башфорта, соответствующие нескольким первым значениям параметра к в формуле (8). Сразу заметим, что при фиксировании к = 0,1, 2,... в (8) тем самым задается степень интерполяционного многочлена (нулевая, первая, вторая и т.д.) и, соответственно, число слагаемых, равное 1, 2, 3, в правой части (9) (или, что то же, в скобках формулы (10)). Конечные разности в получающихся при этом конкретных формулах будем раскрывать через значения функции, приводя формулы к виду, называемому иногда ординатным. Имеем:
при к = 0 
(11)
при к = 1
(12)
при к =2
(13)
при k = 3
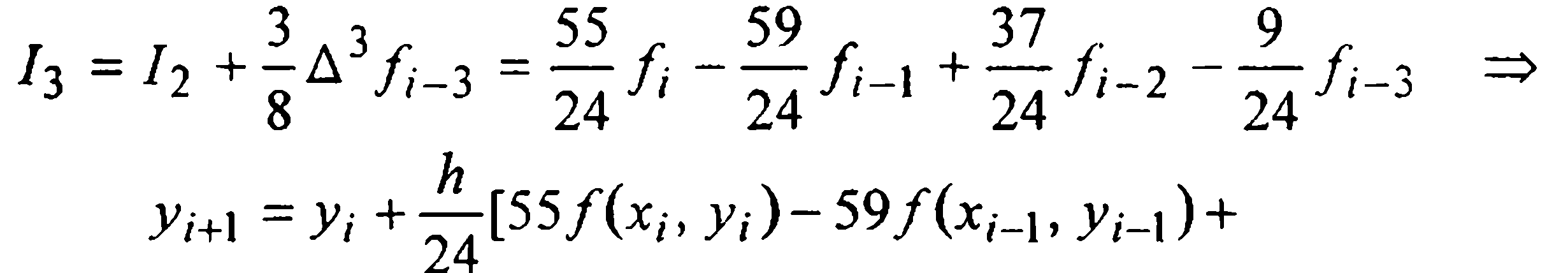
(14)
Формулы (11), (12), (13) и (14) определяют методы Адамса-Башфорта соответственно первого, второго, третьего и четвертого порядков. Относительно порядка метода (11) сомнений нет: мы узнаём метод Эйлера (8).
Интерполяционные методы Адамса-Моултона. В интеграле, фигурирующем в формуле (7), делаем замену
x=xi+1+qh и подставляем в него выражение определяемое формулой (5). Приходим к аналогичному (8) равенству
где
(15)
Отсюда следует конечноразностная формула интерполяционного метода Адамса-Моултона
(16)
Аналогично тому, как это делалось для методов Адамса-Башфорта, при к= 0, 1, 2,3, т.е. фиксированием одного, двух, трех, четырех членов в представлении (15) интеграла 
получаем следующие частные формулы:
при к= 0 
(17)
при к = 1 
(18)
при к=2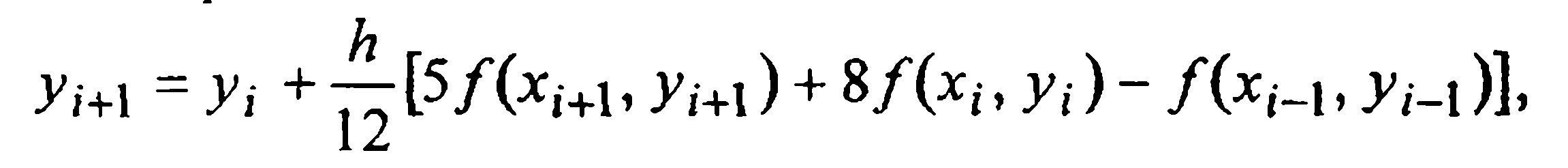 
(19)
при к= 3 
(20)
Формулы (17) и (18) определяют уже известные нам методы, а именно, неявный метод Эйлера (14) и метод трапеций (15), имеющие первый и второй порядки точности соответственно. Заметим, что оба эти метода являются одношаговыми, а следующие за ними методы Адамса-Моултона (19) и (20) третьего и четвертого порядков относятся, как легко видеть, соответственно к двухшаговым и трехшаговым методам. Таким образом, для интерполяционных методов Адамса-Моултона порядок шаговости на единицу ниже порядка точности метода (за тривиальным исключением, отвечающим случаю к = 0).
Важное различие в экстраполяционных и интерполяционных методах Адамса заключается в том, что первые из них являются явными, а вторые — неявными. Эти термины однозначно определяют, о каком из двух семейств методов Адамса идет речь, а их сущность диктует особенности использования методов Адамса при практических расчетах, что найдет отражение в следующем параграфе.
