Метод Эйлера — разные подходы к построению

Учитывая ключевую позицию, которую занимает метод Эйлера в теории численных методов ОДУ, рассмотрим несколько способов его вывода. При этом будем считать, что вычисления проводятся с расчетным шагом расчетными точками (узлами) служат точки х_i = х₀ + ih (i=0,1,..., п) промежутка [ x₀, b ]ицелью является построение таблицы

приближенных значений y_i решения у = у(х) задачи (1)-(2) в расчетных точках х_i.

Геометрический способ. Пользуясь тем, что в точке х₀ известно и значение решения у(х₀) = у₀ (согласно (2)), и значение его производной у'(x_о)=f(x₀, y₀) (согласно (1)), можно записать уравнение касательной к графику искомой функции y= у(х) в точке (х₀;y₀):

(6)

При достаточно малом шаге h ордината

(7)

этой касательной, полученная подстановкой в правую часть (6) значения по непрерывности должна мало отучаться от ординаты у(х₁) решения у(х) задачи (1)-(2). Следовательно, точка (х₁, у₁) пересечения касательной (6) с прямой x=x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую

которая уже приближенно отражает поведение касательной к у=у(х) в точке (х₁,у(х₁)). Подставляя сюда х=х₂(=х₁ + h), иначе, пересекая эту «касательную» прямой х = х₂, получим приближение значения у(х₂) значением

и т.д. В итоге этого процесса, определяемого формулой

i = 0,1,..., п (8)

и называемого методом Эйлера, график решения у = у(х) данной задачи Коши (1)-(2) приближенно представляется ломаной, составленной из отрезков приближенных касательных (рис. 1), откуда происходит другое название метода (8) — метод ломаных.

Рис. 1. Геометрическая интерпретация метода Эйлера

Применение формулы Тейлора. Описываемый здесь способ вывода метода Эйлера тесно связан с предыдущим. Линеаризуя решение вокрестности начальной точки по формулеТейлора, имеем

Отсюда при х = х₁ получаем

(9)

Точное равенство (9), переписанное в виде

говорит о том, что здесь мы имеем одновременно как саму формулу Эйлера для вычисления значения (сравните с формулой (7)), так и ее остаточный член

(10)

где ξ_i — некоторая точка интервала (x₀, x₁).

Остаточный член (10) характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т.е. ошибку, совершаемую на одном шаге. Очевидно, что от шага к шагу, т.е. при многократном применении формулы (8), возможно наложение ошибок. За п шагов, т.е. в точке b, образуется глобальная ошибка. П орядок глобальной ошибки (относительно шага h) на единицу ниже, чем порядок локальной ошибки, а порядком глобальной ошибки и определяется порядок соответствующего численного процесса решения задачи Коши. Таким образом, локальная ошибка метода Эйлера, согласно (10), есть глобальная — 0(h), т.е. метод Эйлера относится к методам первого порядка.

Разностный способ. Рассматривая уравнение (1) в точке x₀ с учетом (2) имеем равенство

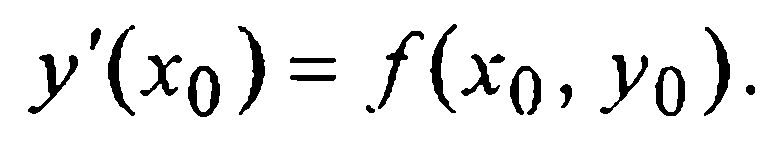
Применяя к его левой части аппроксимацию производной правым разностным отношением первого порядка точности

получаем

что идентично равенству (9), поставляющему формулу для вычисления у₁ вида (7) и локальный остаточный член (10). Ясно, что для получения общей расчетной формулы (8) можно было сразу применить аппроксимацию по формуле (6.16) в равенстве

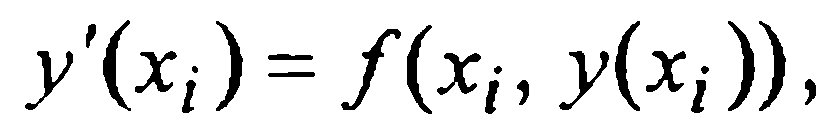(11)

заменив неизвестное точное значение y(x_i) известным приближенным значением y_i.

Заметим, что порядок получающегося таким способом метода численного интегрирования дифференциальной задачи (1)-(2) совпадает с порядком аппроксимации производной в левой части уравнения (1).

Квадратурный способ. Как было показано начальную задачу для ОДУ (1)-(2) можно заменить эквивалентным интегральным уравнением (3). При х=х₁ из него получится равенство

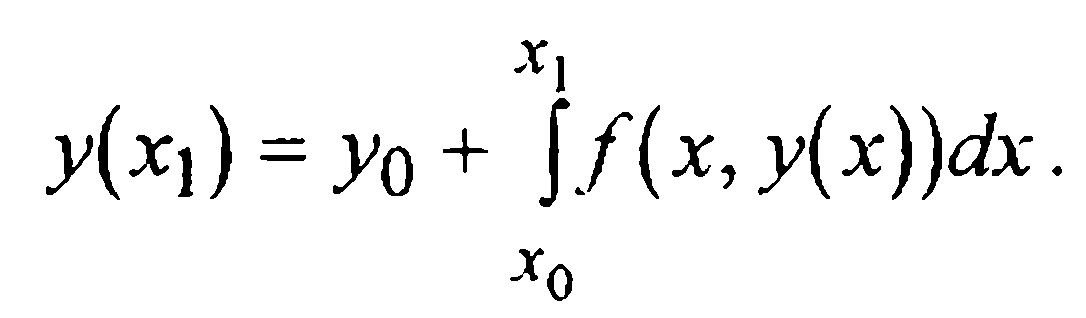(12)

Применение к интегралу в правой части равенства (12) простейшей (одноточечной) формулы левых прямоугольников дает приближенную формулу

правая часть которой, очевидно, совпадает с выражением (7) для подсчета значения у₁. В общем случае расчетная формула (8) метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве

(13)

в предположении, что на каждом i-м шаге в роли начальной точки (x₀,y₀) выступает точка (x_i, y_i). Зная точность используемой в (13) квадратурной формулы, легко прийти к тому же выражению локальной ошибки метода Эйлера, что и при других способах его построения.

Существуют и другие подходы к выводу метода Эйлера. В частности, он будет возникать далее как частный случай некоторых семейств численных методов решения задачи (1)-(2).