Занятие № 16. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Классификация методов. Метод Пикара

Будем рассматривать обыкновенное дифференциальное уравнение (ОДУ) первого порядка

(1)

с начальным условием

y(х₀) = у₀, (2)

где f(x) — некоторая заданная, в общем случае, нелинейная функция двух переменных. Будем считать, что для данной задачи (1)-(2), называемой начальной задачей или задачей Коши, выполняются требования, обеспечивающие существование и единственность на отрезке [х₀,b] ее решения у=у(х).

Несмотря на внешнюю простоту уравнения (1), решить его аналитически, т.е. найти общее решение у=у(х, С) с тем, чтобы затем выделить из него интегральную кривую у=у(х), проходящую через заданную точку (х₀;у₀), удается лишь для некоторых специальных типов таких уравнений. Поэтому, как и в родственной для (1)-(2) задаче вычисления интегралов, приходится делать ставку на приближенные способы решения начальных задач для ОДУ, которые можно разделить на три группы:

1)приближенно-аналитические методы;

2)графические или машинно-графические методы;

3)численные методы.

К методам первой группы относят такие, которые позволя­ют находить приближение решения у(х) сразу в виде некоторой «хорошей» функции φ (х). Например, широко известен метод степенных рядов, в одну из реализаций которого заложено представление искомой функции у(х) отрезком ряда Тейлора, где тейлоровские коэффициенты, содержащие производные высших порядков, находят последовательным дифференцирова­нием самого уравнения (1). Другим представи­телем этой группы методов является метод последовательных приближений, суть которого приведена чуть ниже.

Название графические методы говорит о приближенном представлении искомого решения у(х) на промежутке [x₀,b] в виде графика, который можно строить по тем или иным прави­лам, связанным с графическим толкованием данной задачи. Фи­зическая или, возможно, точнее будет сказать, электротехниче­ская интерпретация начальных задач для определенных видов уравнений лежит в основе машинно-графических методов при­ближенного решения. Реализуя на физико-техническом уровне заданные электрические процессы, на экране осциллографа на­блюдают поведение решений дифференциальных уравнений, описывающих эти процессы. Изменение параметров уравнения приводит к адекватному изменению поведения решений, что по­ложено в основу специализированных аналоговых вычисли­тельных машин (АВМ).

Наконец, наиболее значимыми в настоящее время, характе­ризуемое бурным развитием и проникновением во все сферы че­ловеческой деятельности цифровой вычислительной техники, являются численные методы решения дифференциальных уравнений, предполагающие получение числовой таблицы приближенных значений y_i искомого решения у(х) на некото­рой сетке значений аргумента х. Этим способам и будет посвящено дальнейшее изложение. Что делать с получае­мыми численными значениями решения, зависит от прикладной постановки задачи. Если речь идет о нахождении только значе­ния у(b), тогда точка b включается как конечная в систему рас­четных точек х_i, и все приближенные значения y_i ≈y(x_i), кроме последнего, участвуют лишь как промежуточные, т.е. не требуют ни запоминания, ни обработки. Если же нужно иметь прибли­женное решение у(х) в любой точке х, то для этого к получае­мой числовой таблице значений y_i можно применить какой-либо из способов аппроксимации табличных функций, рассмотренных ранее, например, интерполяцию или сплайн-интерполя­цию. Возможны и другие использования численных дан­ных о решении.

Коснемся одного приближенно-аналитического способа решения начальной задачи (1)-(2), в котором искомое ре­шение у=у(х) в некоторой правой окрестности точки х₀ явля­ется пределом последовательности получаемых определенным образом функций у_п(х).

Проинтегрируем левую и правую части уравнения (1) в границах от х₀ до х:

Отсюда, с учетом того, что одной из первообразных для у'(х) служит у(х), получаем

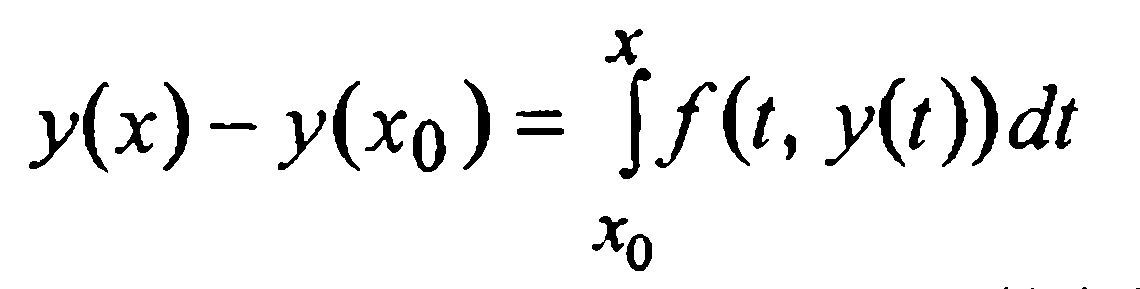
или, с использованием начального условия (2),

(3)

Таким образом, данное дифференциальное уравнение (1) с на­чальным условием (2) преобразовалось в интегральное урав­нение (неизвестная функция здесь входит под знак интеграла).

Полученное интегральное уравнение (3) имеет вид зада­чи о неподвижной точке для оператора Формально к этой зада­че можно применить метод простых итераций

(4)

достаточно обстоятельно рассматривавшийся приме­нительно к системам линейных и нелинейных алгебраических и трансцендентных уравнений. Беря в качестве начальной функции y₀(х) заданную в (2) по­стоянную y₀, по формуле (4) при п=0 находим первое при­ближение

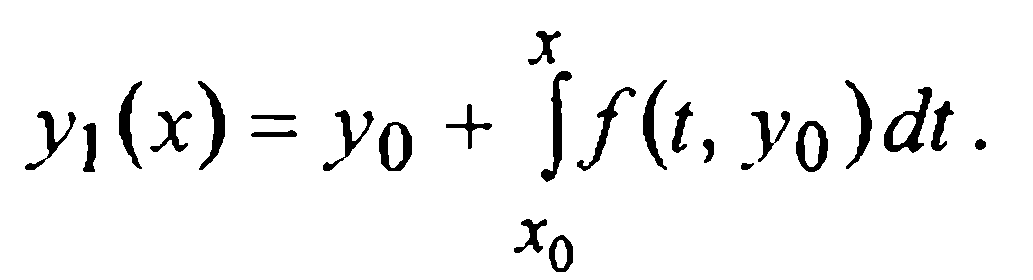
Его подстановка в (4) при п=1 дает второе приближение

и т.д. Таким образом, этот приближенно-аналитический метод, называемый методом последовательных приближений или методом Пикара определяется формулой

(5)

где n=0,1, 2,... и у₀(х)=y₀.

Отметим две характеристики метода последовательных приближений Пикара, которые можно отнести к негативным. Во-первых, в силу известных проблем с эффективным нахождением первообразных, в чистом виде метод (5) редко реализуем. Во-вторых, как видно из вышеприведенного утверждения, этот ме­тод следует считать локальным, пригодным для приближения решения в малой правой окрестности начальной точки. Большее значение метод Пикара имеет для доказательства существования и единственности решения задачи Коши, нежели для его практи­ческого нахождения.