Занятие № 21. Методы прогноза и коррекции

Под названием методы прогноза и коррекции (иначе ме­тоды предсказания и уточнения, предиктор-корректорные методы) понимается совместное применение явных и неявных методов одинакового или смежных порядков. По явной формуле значение решения у(х) задачи (1)-(2) в текущей (расчет­ной) точке х_i+1 прогнозируется, т.е. находится его, быть может, достаточно грубое приближение, а с помощью неявной форму­лы, в правую часть которой подставляется спрогнозированное значение, оно уточняется (корректируется). Пример приближен­ного вычисления у(х_i+1) по такой явно-неявной схеме у нас уже есть: парное использование явного ме­тода Эйлера для предсказания и метода трапеций для уточнения (17).

Остановимся подробнее на методах прогноза и коррекции, базирующихся на парах явных и неявных методов Адамса одинакового порядка. Обозначим через приближенное значение решения y(x_i+1), подсчитываемое по явной экстраполяционной формуле Адамса-Башфорта, и составим несколько пар из рас­смотренных в предыдущем параграфе частных формул Адамса-Башфорта (11), (12), (13), (14) и Адамса-Моултона (17), (18), (19), (20).

Имеем следующие предиктор-корректорные методы Адамса:

первого порядка (он же явно-неявный метод Эйлера)

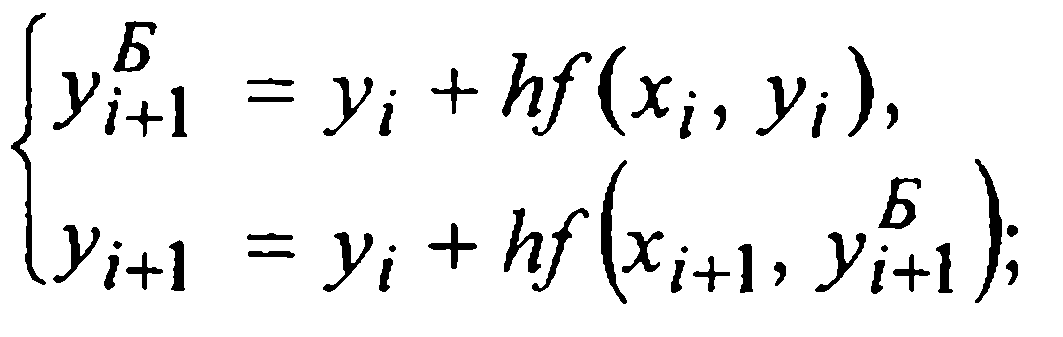
Второго порядка

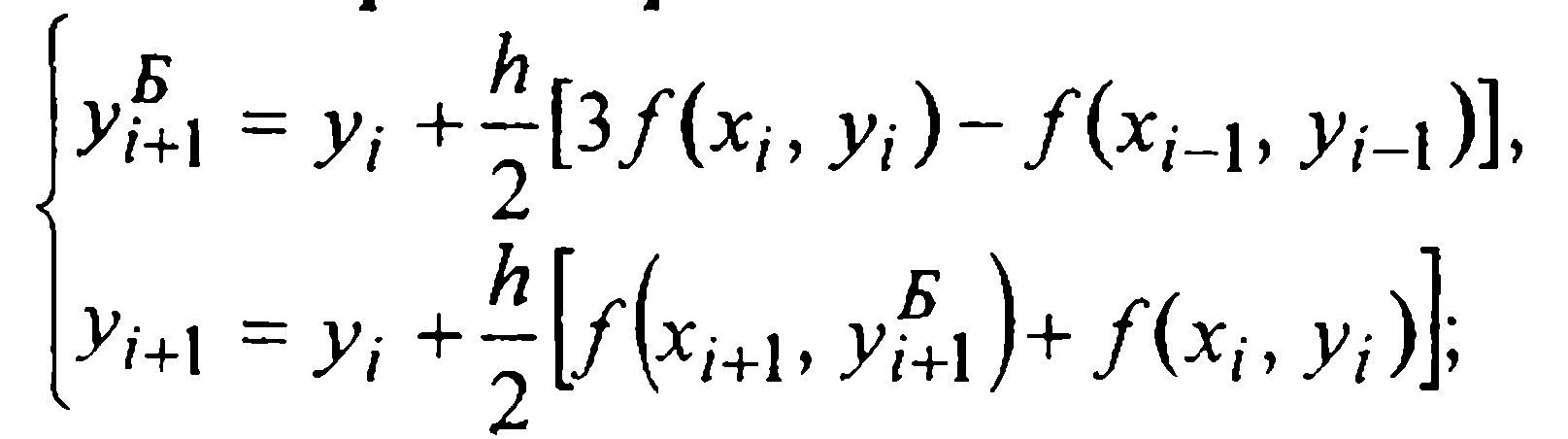
Третьего порядка

Четвертого порядка

(21)

Одним из главных достоинств методов прогноза и коррек­ции является возможность контролировать шаговую погреш­ность сравнением двух полученных по явной и неявной форму­лам приближений к y(x_i+1). Покажем, как реализуется эта воз­можность для наиболее употребительного предиктор-корректор­ного метода Адамса четвертого порядка (21).

Вспомним, что первая из формул (21) была получена из общей формулы Адамса-Башфорта (10), а вторая — из общей формулы Адамса-Моултона (16), в которых последними бра­лись разности третьего порядка (подынтегральная функция в ра­венстве (3) аппроксимировалась интерполяционным много­членом третьей степени). Считая, что расчетный шаг h доста­точно мал и конечные разности с ростом их порядка убывают, главные части шаговых погрешностей формул Башфорта и Моултона четвертого порядка, в соответствии с (10) и (16), характеризуются величинами для явной и для неявной формул. Таким образом, если наряду с введенным обозначением обозначить через прибли­женное значение у(х_i+1), получаемое по формуле Адамса-Моултона четвертого порядка, то можно записать два прибли­женных представления y(x_i+1)^:

(22)

и

(23)

Отсюда видно, что если четвертые разности функции f(x, у(х)) в используемой части табл. 1 конечных разностей практически постоянны (а это можно связать с удачным выбором величины шага h при достаточном запасе знаков в значениях f(x_j,y_j)), то во-первых, значения и дают двусторонние приближения к точному решению y(x_i+1), а во-вторых, через разность между зна­чениями и можно оценить точность каждого из них.

Действительно, приравнивая правые части приближенных равенств (22) и (23) и отождествляя имеем:

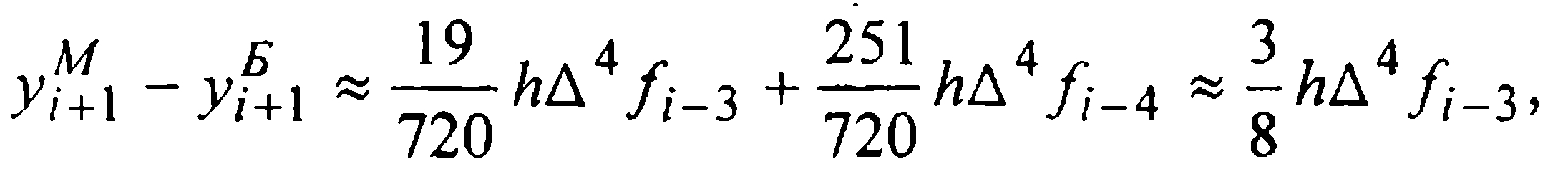
откуда

Подставляя последнее в (23), получаем приближенное равенство

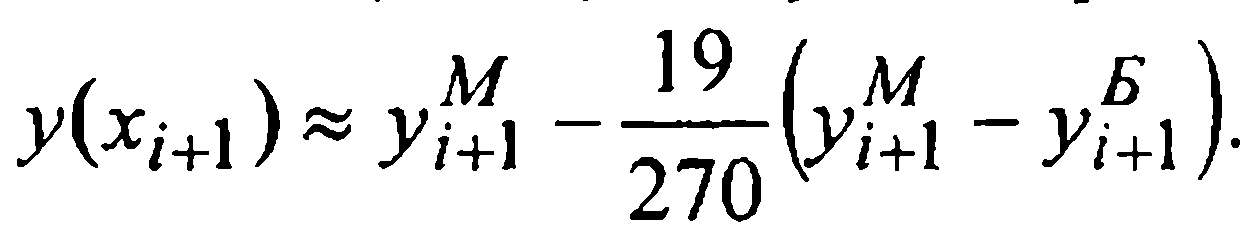(24)

Использование приближенной формулы (24) может быть двояким. Переписав ее в виде

применяем это для пошагового контроля точности:

если то полагаем с точностью ε и переходим к следующему шагу (i:=i+1), иначе уменьшаем шаг h и снова подсчитываем

Другое назначение формулы (24) — это прямое приме­нение ее правой части для получения уточненного значения: полагаем

(25)

Наверное, есть смысл контроль точности делать на каждом шаге, а к уточнению по формуле (25) прибегать при выводе оконча­тельных результатов.

Замечание 1. При выводе формулы (24) под мы понима­ем значение, соответствующее «чистому» методу Адамса-Моултона чет­вертого порядка, т.е. — это точная реализация неявной формулы (20). Вторая же формула предиктор-корректорного метода (21) соот­ветствует лишь одному приближению к по методу простых итераций, где в качестве начального приближения берется . Поэтому примене­ния формулы (24) к методу прогноза и коррекции (21) будут убеди­тельны в том случае, если его вторая формула итерируется хотя бы один-два раза. Однако, чем больше таких итераций, тем ниже вычислительная эффективность этого метода, в целом весьма высокая по сравнению с мно­гоэтапными методами Рунге-Кутты.