Желая, чтобы интерполяционный многочлен Лагранжа Ln( х)в целом хорошо приближал функцию у= f(x) на отрезке [а, b], поставим вопрос: как расположить на нем n+1узлов интерполяции хi, (i= 0, 1, …, n), чтобы при этом минимизировать максимальную на [а,b] погрешность?
Максимальная погрешность интерполирования достаточно гладкой функции на отрезке [-1, 1] многочленом п-й степени будет минимальной, когда в качестве узлов интерполяции 
берутся корни многочлена Чебышева Tn+1(t). Будем называть их чебышевскими узлами интерполяции.
Знание экстремальных значений многочлена Чебышева позволяет уточнить величину максимального отклонения Ln(x) от f(x) при таком выборе узлов, т.е. когда точки ti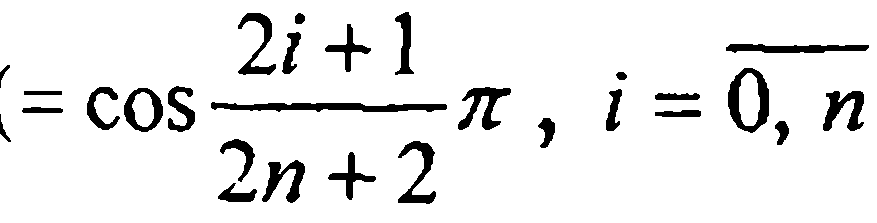 
есть корни 
a 
А именно,
Эта оценка называется наилучшей равномерной оценкой погрешности интерполяции.
Если функция f(x) бесконечно дифференцируема на [а, b] и в качестве узлов интерполяции берутся корни многочленов Чебышева (приведенные к отрезку [а, b], то
Обобщением этого факта для непрерывных (необязательно дифференцируемых) функций и произвольных (не обязательно интерполяционных) многочленов является широко известная в математическом анализе теорема.
Теорема (Вейерштрасса). Для любой непрерывной на [а, b] функции f(x) найдется многочлен Qn(x) такой, что
Доказано, что для любой функции f(x) существует единственный многочлен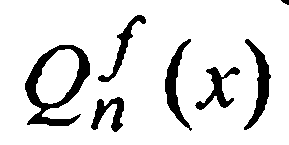 
такой, который из всех многочленов Qn(x) степени n наилучшим образом аппроксимирует на [а, b] функцию f(x), минимизируя максимальное расстояние между f(x) и Qn(x). Этот многочлен, т.е. многочлен 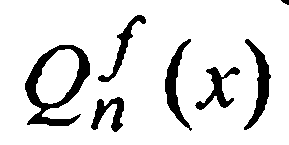такой, что
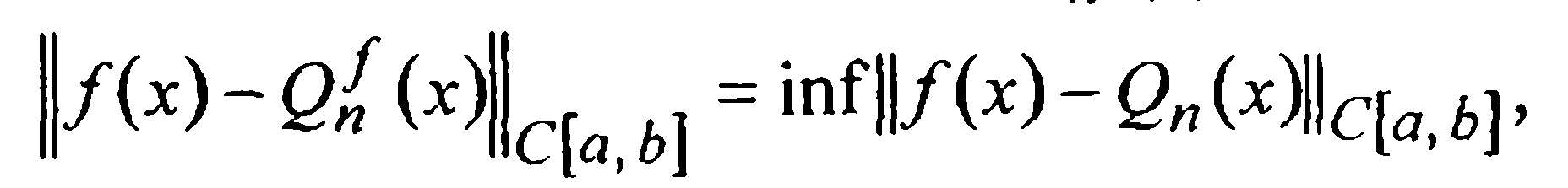
называется многочленом наилучшего равномерного приближения для f(x) на [а, b] или ее чебышевским приближением.
Одним из характеристических свойств многочленов наилучших равномерных приближений является критерий Чебышева. Его отражает следующая теорема.
Теорема (Чебышева). Многочлен 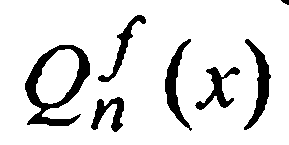является многочленом наилучшего равномерного приближения для функции f(x) тогда и только тогда, когда на [а, b] существует не менее n + 2 точек хi таких, что в них поочередно принимаются наибольшие положительные и отрицательные отклонения, т. е. поочередно разностьf (xi) - 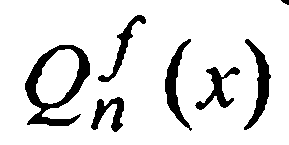равна Е или - Е, где
Эта теорема говорит о том, что максимальная ошибка аппроксимации функции многочленом наилучшего равномерного приближения реализуется в числе точек, большем, по меньшей мере, на 2, чем степень многочлена, причем знаки ошибки чередуются. Точки хi, в которых реализуется максимальное отклонение многочлена 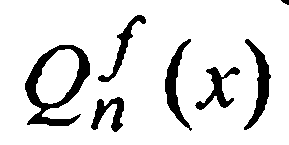от f(x) на [а, b], называются точками чебышевского альтернанса.
К сожалению, неизвестны ни общий вид многочленов наилучших равномерных приближений, ни способы их построения, имеются лишь некоторые методики построения многочленов, близких к наилучшим равномерным, а также способы построения чебышевских приближений невысокого порядка для нескольких весьма узких классов функций. Последние существенно опираются на приведенную теорему о чебышевском альтернансе, что демонстрируется в следующих двух простейших случаях.
Случай А. Пусть функция f(х) непрерывна на [a,b], и пусть для нее требуется построить многочлен наилучшего равномерного приближения нулевой степени. Обозначим этот приближающий многочлен через 
Он определяется всего одним параметром: 
. Чтобы найти значение этого параметра для заданной функции f(х), воспользуемся тем свойством непрерывной на замкнутом промежутке функции, согласно которому на нем всегда найдутся, по крайней мере, две точки, в которых она принимает свои наименьшее и наибольшее значения.
Пусть 
Тогда совершенно очевидно, что полагая 
т.е. подменяя функцию f(x) функцией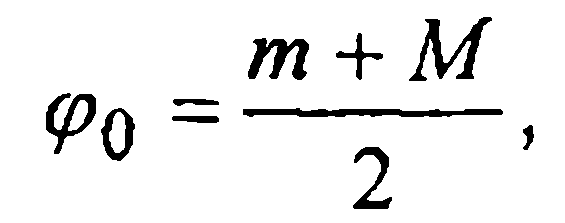 
будем иметь максимальное отклонение
причем точки отрезка [а, b], в которых оно реализуется — это точки, где принимаются значения т и М. В силу непрерывности f(х), локальные минимумы и максимумы должны чередоваться; по меньшей мере, два из них определяют точки чебышевского альтернанса (с чередованием знаков разностей f(x)- 
). Поэтому не существует другой постоянной, которая приближала бы f(x) на [а, и] лучше, чем постоянная .
Случай Б. Пусть аппроксимируемая функция f(x) дифференцируема и выпукла (в широком смысле) на отрезке [а, b], a аппроксимирующая ее функция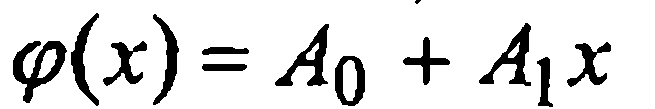 
— многочлен наилучшего равномерного приближения первой степени. Чтобы найти его коэффициенты следует изучить разность между f(x) и φ(х), т. е. функцию 
Так как функция f(x) по предположению выпукла, а сдвиг на линейную функцию A0 + А1х не изменяет выпуклости, то и функция u(х) выпукла на [а, b]. Следовательно, существует единственная точка с∈[а, b ], в которой u(х) имеет минимум; если u(х) выпукла вверх, то в точке с должен быть максимум u(х). В любом случае, точка с∈[а, b ] есть точка экстремума u(х), и за счет возможности варьирования коэффициентов функции φ(х) (точнее, коэффициента А1) можно считать, что точка с является внутренней точкой отрезка [а, b].
Потребуем, чтобы точки а, с и b в указанной последовательности составляли чебышевский альтернанс, т. е. чтобы в них последовательно принимались значения Е, - Е, Е или - Е, E, -E, где 
— максимальная погрешность аппроксимации функции f(x) функцией φ (х). Добавляя к этим требованиям еще необходимое условие экстремума дифференцируемой функции u(х) в точке с и возвращаясь к исходным функциям, приходим к системе четырех уравнений относительно четырех неизвестных A0, А1, Е и с (из которых, в основном, лишь первые три неизвестные представляют интерес):
Получить решение такой системы в общем виде не представляется возможным, поскольку неизвестная величина с входит в нее нелинейным образом (в каждом конкретном случае подобная система без проблем решается численно).
Пример. Построим многочлены наилучшего равномерного приближения нулевой и первой степеней для функции y = sinx на отрезке [0, π/6].
Сразу заметим, что данная функция всюду дифференцируема (а значит, непрерывна) и выпукла вверх на заданном отрезке. При этом
Следовательно, согласно рассмотренному выше случаю А, найдя
при х∈ [0, π/6] можно считать, что sinх ≈ 0.25 с предельной погрешностью 0.25.
Далее, в соответствии со случаем Б, продифференцировав данную функцию, составляем систему:
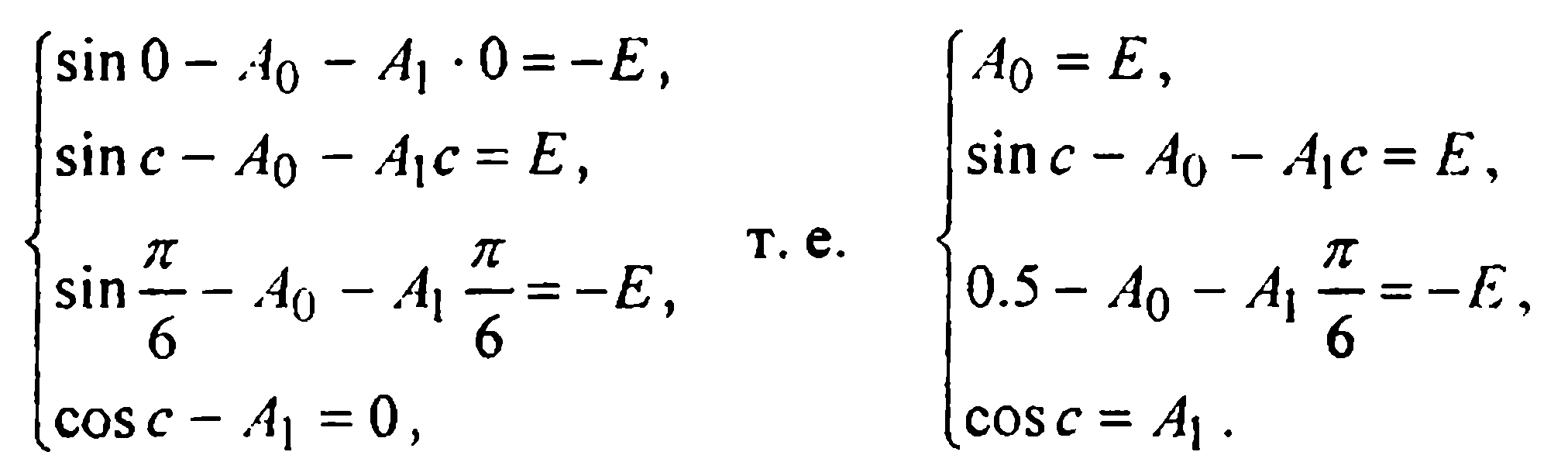
Из нее последовательно находим:
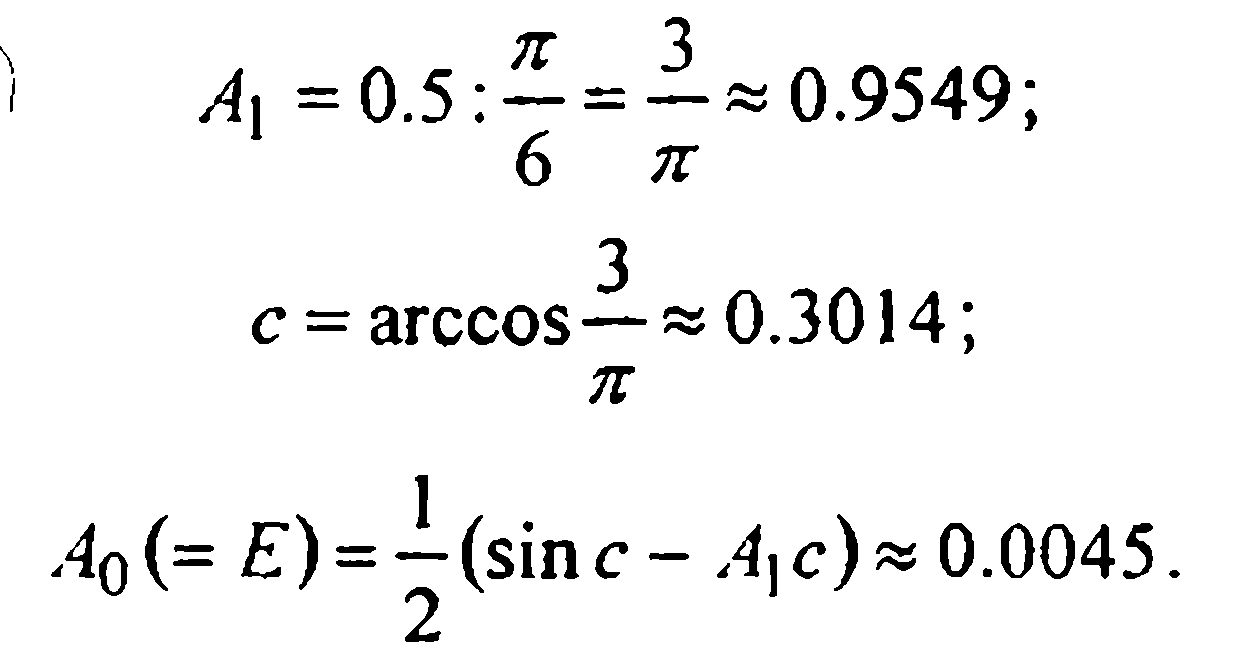
Таким образом, функцию y = sinx на отрезке [0, π/6] можно подменить линейной функцией у = 0.0045 + 0.9549x, и наибольшая ошибка при этом не будет превышать величины ≈0.0045.
Задания: выполнить задание 2 и 3 ИДЗ№2.
