Занятие № 10. Интерполяционный многочлен Ньютона. Многочлены Чебышева

Конечные разности

Зададимся целью придать интерполяционной формуле бо­лее простой вид, подобный виду широко используемой в матема­тическом анализе формулы Тейлора. Если в интерполяционном многочлене Лагранжа (6) все слагаемые однотипны и играют одинаковую роль в образовании результата, хотелось бы иметь такое представление интерполяционного многочлена, в котором, как и в многочлене Тейлора, слагаемые располагались бы в по­рядке убывания их значимости. Такая структура интерполяцион­ного многочлена позволила бы более просто перестраивать его степень, добавляя или отбрасывая удаленные от начала его запи­си члены.

Поставленной цели будем добиваться сначала для несколь­ко суженной постановки задачи интерполяции. А именно, будем считать, что интерполируемая функция у = f(x) задана своими значениями на системе равноотстоящих узлов т.е. таких, что любой узел х_i, этой сетки можно представить в виде

х_i = х₀ + ih,

где i=0, 1, …, п, a h>0 — некоторая постоянная величина, называемая шагом сетки (таблицы).

Прежде чем строить желаемые интерполяционные форму­лы, рассмотрим элементы теории конечных разностей.

Вычитая из каждого последующего члена конечной после­довательности из n+1 чисел предыдущий, образу­ем п конечных разностей первого порядка

или, проще, п первых разностей данной табличной функции. Из них, в свою очередь, таким же образом можно получить n-1 ко­нечных разностей второго порядка, или вторых разностей:

Этот процесс построения разностей может быть продолжен, и весь он, очевидно, описывается одной рекуррентной формулой, выражающей конечную разность к-го порядка через раз­ности (к - 1)-го порядка:

где к = 1, 2, …, п и

В некоторых случаях требуется знать выражения конеч­ных разностей непосредственно через значения функции лежащей в их основе. Для нескольких первых порядков разно­стей их можно получить прямой подстановкой:

Подметив закономерность в коэффициентах рассмотренных представлений конечных разностей, записываем общую формулу

(1)

которая может быть строго обоснована методом математической индукции и которая напоминает биномиальное разложение для (у - 1)^к.

Привлекая определение производной, можно обнаружить прямую связь между конечными разностями и производны­ми. А именно, если учесть, что

то можно сказать, что при малых h имеет место приближенное равенство

т.е. первые разности характеризуют первую производную функ­ции f(x), по значениям которой они составлены. Пользуясь этим, имеем для вторых разностей:

т.е. и, вообще,

(2)

Таким образом, на конечные разности можно смотреть как на некоторый аналог производных. Отсюда справедливость многих их свойств, одинаковых со свойствами производных.

Отметим лишь простейшие свойства конечных разностей:

1) конечные разности постоянной равны нулю;

2) постоянный множитель у функции можно выносить за
знак конечной разности.

3) конечная разность от суммы двух функций равна сумме
их конечных разностей в одной и той же точке.

Свойства 2 и 3 характеризуют операцию взятия конечной разности как линейную операцию.

Учитывая роль, которую играют многочлены в теории интерполирования, посмотрим, что представляют собой конечные разности многочлена.

Поскольку многочлен в своей канонической форме есть ли­нейная комбинация степенных функций, положим сначала у=х^п. Используя биномиальное разложение п-й степени дву­члена, получим:

т.е. первая конечная разность степенной функции у=х^п есть многочлен степени п -1 со старшим членом Если взять теперь конечную разность от функции

(3)

то, в силу линейных свойств Δу, можно записать

Первое слагаемое в этой сумме, как выяснено, есть многочлен (n-1)-й степени, второе, аналогично, — многочлен степе­ни п -2, и т.д. Следовательно, первая конечная разность много­члена (3) в точке х с шагом h есть тоже многочлен со стар­шим членом a₀nhx^n-1, вторая конечная разность — многочлен со старшим членом a₀n(n-1)h²x^n-2,…, к-я разность — многочлен со старшим членом а₀п(п-1)...(n-к + 1)h^kx^n-k.

При к = п получаем постоянную разность п-го порядка

для многочлена (3); конечные разности более высоких поряд­ков, естественно, равны нулю.

Итак, главный вывод из предыдущих рассуждений: п-е ко­нечные разности многочлена п-й степени постоянны, а (п+1)-е и все последующие равны нулю.

Более важным для понимания сути полиномиального интерполирования является утверждение, обратное сделанному выше выводу. А именно, что если конечные разности п -го порядка некоторой функции у=у(х) постоянны в любой точке х при различных фиксированных шагах h, то эта функция у(х) есть многочлен степени п.

Для функции у = f(x)_y заданной таблицей своих значений в узлах где конечные разности разных порядков удобно помещать в одну общую таб­лицу с узлами и значениями функции (последние можно интер­претировать как конечные разности нулевого порядка). Эту общую таблицу называют таблицей конечных разностей.

Пример. Составим таблицу конечных разностей для функции у = xln²x по ее значениям, вычисленным с тремя знаками после запятой в точках x_j=0.4 + 0.2 j, где j=0, 1,..., 10.

Абсолютные величины конечных разностей сначала убывают с увеличением их порядка, а затем начинают увеличи­ваться. Это типичное поведение конечных разностей при ограничен­ной точности задания значений сеточной функции.

Природу наблюдаемого в примере поведения модулей конечных разностей нетрудно понять. Если шаг достаточно мал, а данная табличная функция — достаточно гладкая, то сначала с увеличением k в си­лу упомянутой связи (2). Когда эти величины становятся дос­таточно малыми, большую роль начинают играть продукты взаимодействия исходных ошибок округления (так называемый шум округлений).

Что происходит с одной отдельно взятой ошибкой величи­ны ε у значения y_i, можно проследить по таблице. Как видим, с ростом порядка разностей она «расползается» по таблице и уве­личивается по абсолютной величине.

Погрешности, имеющиеся у каждого из данных значений функции, с ростом порядка разностей все больше взаимодейст­вуют.

Из сделанных наблюдений напрашивается следующий вывод. Если какой-то столбец в таблице конечных разностей (в ее эксплуатируемой части) состоит из чисел, абсолютные величины которых составляют всего несколько единиц десятичного знака, являющегося последним в записи исходных значений функции, скажем, не превосходят величины 10ε, где ε — абсолютная по­грешность исходных данных, то эти конечные разности и разно­сти всех последующих порядков не несут практически никакой информации о функции, и их не следует использовать. Разности же предшествующего столбца называются практически посто­янными, и их порядок определяет степень многочлена, которую можно и должно использовать для идеальной в данных условиях полиномиальной интерполяции.

Вспоминая о том, что многочлен k-й степени имеет k-е разности постоянными, а все последующие — нулевыми, прихо­дим к заключению, что если k-е разности таблицы конечных разностей некоторой функции практически постоянны, то эта функция ведет себя в рассматриваемой области, как многочлен k-й степени; эту степень и следует применять для интерполиро­вания с наибольшей для данных реалий точностью.

Обратимся к таблице нашего примера. Видим, что если исключить из рассмотрения верхнюю диагональную строку, то для всей остальной части таблицы третьи разности удовлетворят условию (где 0.0005 — предельная абсолютная погрешность значений y_i). В такой ситуации разности более высоких порядков не сле­довало вообще вычислять, а разности второго порядка можно считать практически постоянными, т.е. для подсчета любых промежуточных зна­чений данной функции, за исключением, быть может, тех, которые нахо­дятся вблизи узла x₀= 0.4, нужно применять квадратичную интерполя­цию.

Конечноразностные интерполяционные формулы

Пусть функция у=f(x) задана на сетке равноотстоящих узлов х_i=х₀+ ih, где i= 0, 1, …, п, и для нее построена таблица конечных разностей.

Будем строить интерполяционный много­член P_n(х) в форме

(4)

Его п+1 коэффициент а₀, а₁, ….,а_п будем находить последова­тельно из п+1 интерполяционных равенств

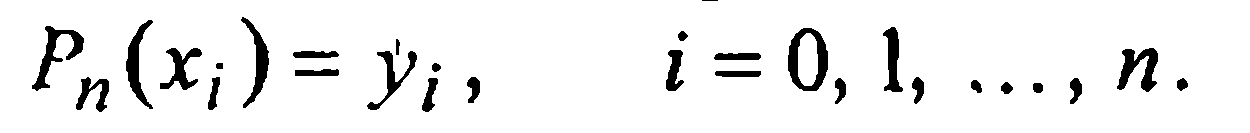
А именно, полагая i=0, т.е. х=х₀ в (4) имеем а по условию интерполяции Р_п(х₀)=у₀, следова­тельно, а_о =у₀.

Далее, при i = 1 аналогично получаем равенство

в которое подставляем уже найденное значение Разре­шая это равенство относительно а₁ и используя обозначение ко­нечной разности, получаем

Следующий шаг, при i = 2, дает:

Полной индукцией можно показать справедливость выражения

(5)

Подставляя найденные коэффициенты (4), получаем многочлен

(6)

который называют первым интерполяционным многочленом Ньютона.

Учитывая, что каждое слагаемое многочлена (6), начи­ная со второго, содержит множитель x-x₀, естественно предпо­ложить, что этот многочлен наиболее приспособлен для интер­полирования в окрестности узла х_0. Будем называть узел x₀ базовым для многочлена (6), и упростим (6) введением новой переменной q равен­ством или (что то же) равенством х=x₀+qh. Так как h при любых i=0, 1,..., n

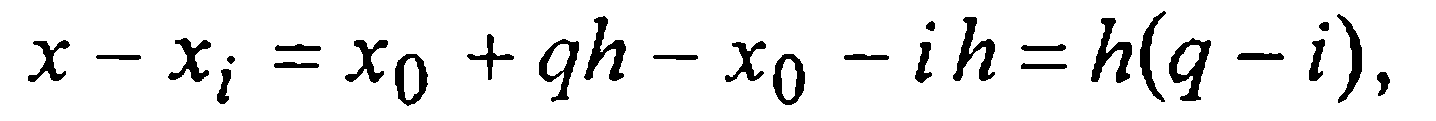
то в результате подстановки этих разностей в (6) приходим к первой интерполяционной формуле Ньютона в виде

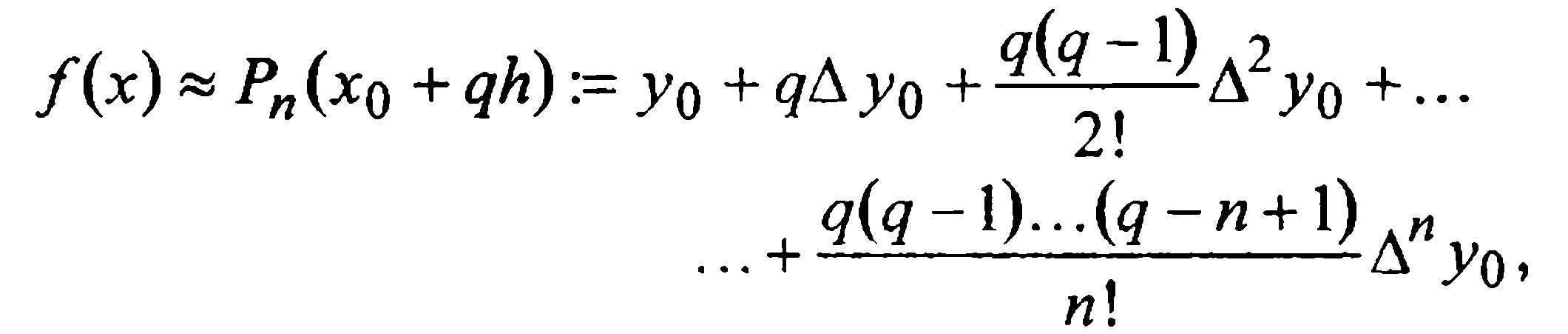(7)

где обозначение указывает не только на п-ю степень многочлена, но и на базовый узел x₀ и связь переменных х и q.

Первая формула Ньютона (7) обычно применяется при значениях |q|<1, а именно, для интерполирования вперед, (при т.е. при ) и экстраполирования назад (при х < х₀, т.е. при q < 0).

Так как, реально степени интерполяционных многочленов бывают не так велики, в то время как таблицы значений функций достаточно обширны, и так как в реальной числовой таблице ни­каких индексов — номеров узлов нет, то за базовый для формулы (7) узел x₀ можно принимать узел, ближайший к заданной фиксированной точке х, если за ним имеется достаточное число узлов для по­строения необходимых для (7) разностей. Поскольку в первой формуле Ньютона используются нисходящие диагонали таблицы конечных разностей, то такое смещение узла, при­нимаемого за базовый, в конце таблицы будет неприемлемо.

Учет этого обстоятельства приводит к потребности в сим­метричной, в определенном смысле, для (7) формулы, которая была бы пригодной для интерполирования в конце таблицы. Для этого, в отличие от (4), форма интерполяционного многочлена Р_п(х) берется такой, которая предусматривает поочередное под­ключение узлов в обратном порядке: сначала последний, потом предпоследний и т.д., т.е.

Коэффициенты этого многочлена находятся анало­гично тому, как они находились для многочлена (4), только здесь подстановка узловых точек вместо х и рассмотрение ин­терполяционных равенств производится тоже в обратном поряд­ке. Полагая имеем:

и т.д. В общем случае

Таким образом, получаем второй интерполяционный мно­гочлен Ньютона

(8)

в котором базовым является узел х_п и коэффициенты которого определяются конечными разностями, расположенными на вос­ходящей от у_п диагонали.

Положим в (8) х=х_п+qh, иначе, введем новую переменную и преобразуем к ней входящие в (8) разности:

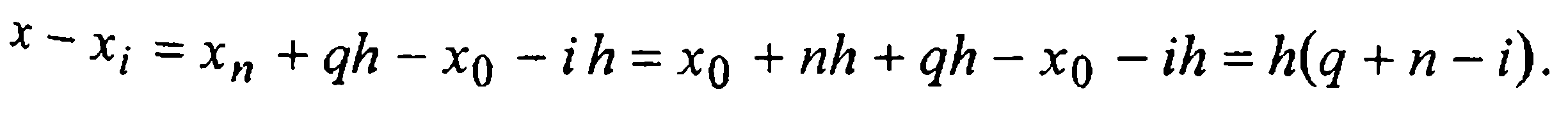
В результате приходим ко второй интерполяционной формуле Ньютона вида

(9)

Ее также целесообразно использовать при значениях |q|<1 т.е. в окрестности узла х_n для интерполирования назад (при q∈(-1, 0)) н экстраполирования вперед (при q> 0).

Наряду с выведенными специально для начала и конца таблицы первой и второй интерполяционными формулами Ньютона, имеется еще несколько формул, рассчитанных на их применение в центральной части таблицы и потому называемых централь­ными интерполяционными формулами. Прежде, чем опреде­лять эти формулы, введем понятие центральных разностей.

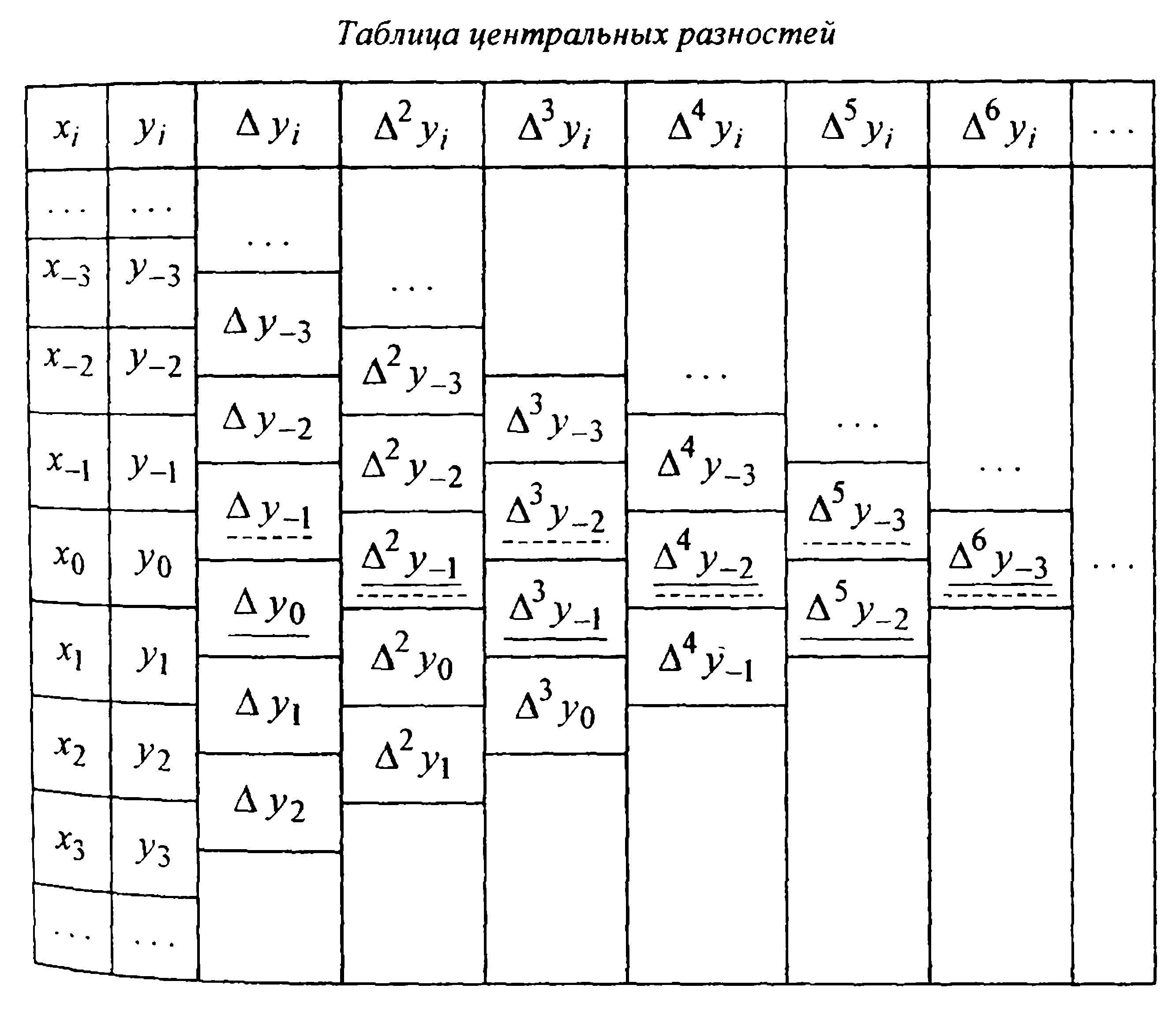
Будем считать, что узел x₀ расположен в середине табли­цы, и нумерация остальных узлов производится, начинаясь с х₀, с использованием как положительных, так и отрицательных ин­дексов, т.е. считаем х_i=х₀+ih, где i= 0, ±1, ±2,.... Тогда цен­тральная часть таблицы конечных разностей будет проиндекси­рована так, как это показано в таблице.

Все подчеркнутые в ней конечные разности (находящиеся с в одной строке и на полстроки выше и ниже) называются центральными разностями.

 

Интерполяционный многочлен ищем в форме

(10)

предполагающей постепенное подключение узлов х_i: сначала при i=0, затем при i=1, потом при i= -1 и т.д., т.е. с двух сто­рон от х₀. При этом здесь и далее не будем фиксировать степени многочленов и не будем стремиться выписывать общие и, тем более, последние члены таких многочленов. Как и в предыдущих случаях, коэффициенты находим один за другим последовательной подстановкой в Р(х) и в интерполяци­онные равенства значений

и т.д. Введя новую переменную и выразив через нее разности для всех i = 0, ± 1, ± 2,..., в результате подстановки этих разностей и выражений коэффициентов в шаб­лон (10), приходим к первой интерполяционной формуле Гаусса

(11)

Записанные слагаемые легко дополнить следующими, если знать, что в этой формуле используются нижние центральные разности все возрастающих порядков, т.е. те, которые подчерк­нуты в табл.1 сплошной чертой.

Таблица 1

Совершенно аналогично, подключая узлы в другом порядке после x₀ сначала предшествующий, затем последующий и т.д., т.е. 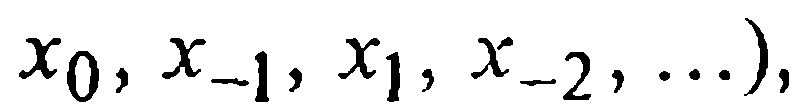можно построить вторую интерполяционную формулу Гаусса

(12)

использующую верхние центральные разности (подчеркнутые в табл.1 пунктирной линией).

Интерполяционные формулы Гаусса служат полуфабрика­тами для получения более симметричных, использующих все центральные разности интерполяционных формул.

Так, полусумма первого и второго интерполяционных мно­гочленов Гаусса после преобразований приводит к формуле

(13)

называемой интерполяционной формулой Стирлинга К.

Если же взять полусумму второго интерполяционного мно­гочлена Гаусса и такого же многочлена, но с нижними индекса­ми, увеличенными на единицу (т.е. с базовой точкой х₁ вместо x₀), то придем к интерполяционной формуле Бесселя

(14)

В последней формуле обращает на себя внимание тот факт, что она сильно упростится, если в нее подставить значение q=1/2, соответствующее значению аргумента

Этот частный случай формулы Бесселя называют формулой ин­терполирования на середину:

(15)

Итак, если точка х, в которой нужно найти приближенное значение таблично заданной функции f(х), находится в начале или в конце таблицы, применяется соответственно первая (7) или вторая (9) формулы Ньютона с таким выбором ба­зовой точки, чтобы значение |q| было как можно меньше. Если точка х находится в середине таблицы, то всегда можно за­фиксировать точку x₀ в таблице центральных разностей так, чтобы 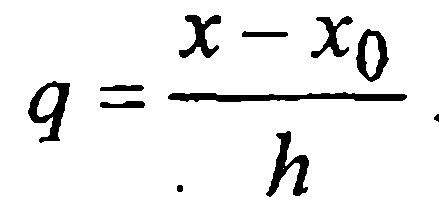либо было по модулю меньше 0.25 и тогда при­менять интерполяционную формулу Стирлинга (13), либо что­бы q ∈[0.25, 0.75] и использовать формулу Бесселя (14).

Пример. Пусть требуется для функции у = f(x), заданной в предыдущем примере таблицей нескольких своих значений с тремя знаками после запятой, найти приближенные значения: а) f(0.5); б) f(1.22); в) f(0-5); г) f(1.94); д) f(2.5), записав предварительно соответст­вующие каждому случаю интерполяционные формулы.

Для решения поставленной задачи учитываем, что значения f(x) заданы на сетке равноотстоящих узлов, поэтому здесь можно применить конечноразностную интерполяцию. При этом бу­дем пользоваться уже составленной таблицей конечных разностей и прове­денным ранее ее анализом на выявление оптимальной степени многочле­на. Для случаев б-д фиксируем вторую степень, для а — третью. В каждом случае, т.е. для конкретного значения аргумента, выбираем базо­вый узел, подсчитываем значение вспомогательной переменной q и, в за­висимости от положения базового узла и значения q, пользуясь представ­ленными в таблице числами, записываем требуемую интерполяционную формулу. Подстановка в нее значения q приводит к искомому значению

а) При x=0.5 (начало таблицы) полагаем х₀=0.4; тогда 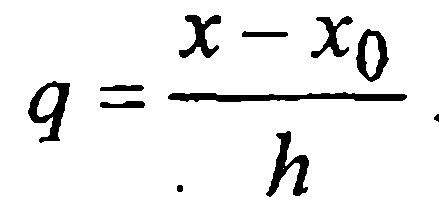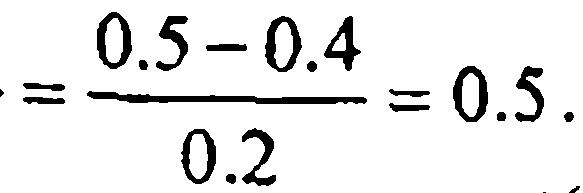Соответствующую интерполяционную формулу для аппроксимации f(x) при х=0.4 + 0.2q с q∈(-1,1) записываем, глядя на первую интерполяционную формулу Ньютона (7) и таблицу значений:

Отсюда получаем искомое значение

б) Точка х=1.22 находится в средней части таблицы. Поэтому здесь
целесообразно применить формулу Стирлинга или Бесселя. Полагая и найдя останавливаемся на формуле Стирлинга (13), которая в данном случае имеет вид

и при q = 0.1 приводит к искомому значению

в) Здесь, очевидно, напрашивается применение формулы (15)
интерполирования на середину. Полагая имеем:

г) Глядя на положение точки х=1.94 в заданной системе узлов, видим, что для вычисления f(1.94) также возможно применение
центральных интерполяционных формул. Положив х₀=1.8 и вычислив 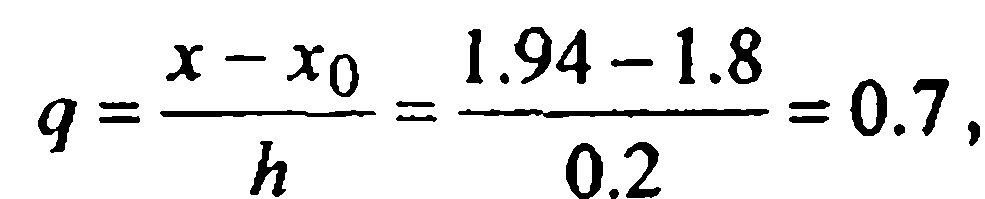на основе (14) записываем интерполяцион­ную формулу Бесселя

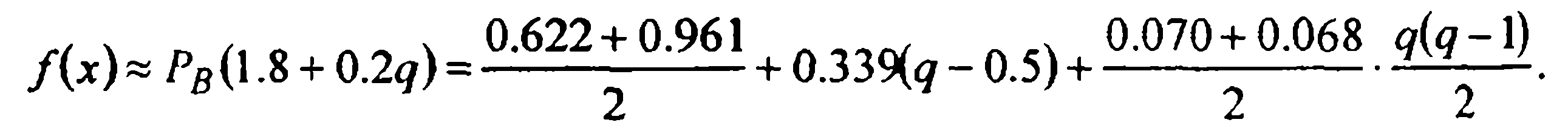
Из нее получаем

д) Точка х = 2.5 расположена за последним узлом, поэтому для экстраполяции f(x) здесь однозначно следует применить вторую интерполяционную формулу Ньютона (9). Считая х_п =2.4 (индекс п здесь ис-
пользуется условно, без придания ему конкретного значения), записываем
формулу экстраполяции

откуда при 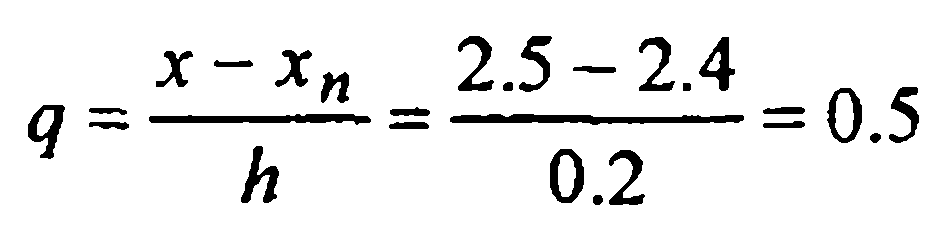находим