Занятие № 9. Равномерное приближение функций многочленами. Интерполяционный многочлен Лагранжа

В основе большинства численных методов математического анализа лежит подмена одной функции f(x) (известной, неиз­вестной или частично известной) другой функцией φ(х) близ­кой к f(x) и обладающей «хорошими» свойствами, позволяю­щими легко производить над нею те или иные аналитические или вычислительные операции. Будем называть такую подмену аппроксимацией или просто приближением функции f (x) функцией φ(х). Для того, чтобы построить какую-то разумную теорию таких приближений и предложить конкретные способы получения аппроксимирующих функций φ (х) по заданным тем или иным образом аппроксимируемым функциям f(x), предва­рительно следует ответить на ряд вопросов.

1) Что известно о функции f(x)? Задана ли она своим ана­литическим выражением или таблицей своих значений, какова степень ее гладкости и доступны ли значения ее производных, как расположены точки в интересующей части области опреде­ления f(x), где известны ее значения, и можно ли их задавать по своему усмотрению, и т.п.

2)Какому классу {семейству) функций должна принадле­жать функция φ(х)? Какие дополнительные требования предъ­являются к φ(х), выделяющие ее из заданного класса?

3) Что понимать под близостью между f(x) и φ(х); ина­че, какой принять критерий согласия между ними? Говоря язы­ком функционального анализа, по метрике какого пространства должно быть малым расстояние между f(x) и φ(х)?

Как видим, задача аппроксимации функции f(x) функци­ей φ(х) состоит в построении для заданной функции f(x) такой функции φ(х), что

(1)

причем левая часть приближенного равенства (1) должна быть обусловлена ответами на вопросы первой группы, правая часть — второй группы, а ответ на вопрос 3) должен уточнить значе­ние связывающего f(x) и φ(х) символа «≈».

Прежде всего, определимся с ответом на второй вопрос. До­говоримся использовать в качестве аппроксимирующих функ­ций φ(х) только многочлены или функции, составленные из многочленов в таком случае будем говорить о полиномиальной аппроксимации или кусочно-полиномиальной аппроксимации соответственно.

По сравнению с другими семействами функций, пригодных для построения теории приближений, например, таких, как три­гонометрические или показательные функции, рациональные функции, для вычислительной математики многочлены привлекательны тем, что они являются линейными функциями своих параметров (коэффициентов), и их вычисление сводится к выполнению конечного числа простейших арифмети­ческих операций — сложения и умножения.

Будем считать, что аппроксимация функции f(x) производится с помощью многочленов степени п∈N₀. Тогда в зависи­мости от выбора критерия согласия и, в частности, от количества точек согласования f(x) с φ(х) (будем называть их узлами), т.е. точек, в которых известна информация об f(x) и, возможно, ее производных, можно рассмотреть разные конкретные способы аппроксимации.

Таблица 1

Интерполяционный многочлен Лагранжа

Пусть в точках таких, что известны значения функции у=f(x), т.е. на отрезке [а, b] задана табличная (сеточная) функция

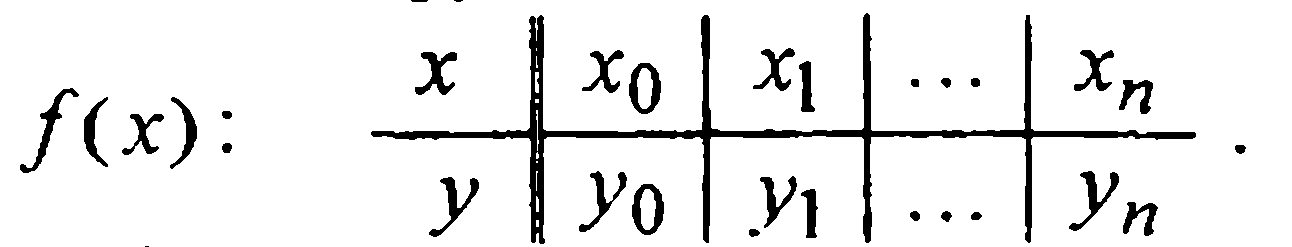(2)

Функция φ(х) называется интерполирующей или интер­поляционной для f(x) на [а, b], если ее значения в заданных точках х₀, х₁, …, х_п, называе­мых узлами интерполяции, совпадают с заданными значениями функции f(x), т.е. с у₀, у₁, …, у_n соответственно. Геометри­чески факт интерполирования означает, что график функции φ(х) проходит так, что, по меньшей мере, в n+1 заданных точ­ках он пересекает или касается графика функции f (х) (рис.1).

Рис.1. Геометрическая интерпретация задачи интерполирования

Легко представить, что таких графиков φ( х), проходящих через заданные точки, можно изобразить сколько угодно, и они могут отличаться от графика f(x) сколь угодно сильно, если не накладывать на φ(х) и f(x) определенных ограничений.

Будем считать, что интерполяционная функция φ(х) есть много­член степени п. Тогда задача интерполяции, точнее, полино­миальной, алгебраической или параболической интерполяции (поскольку график любого многочлена называют параболой) формулируется так:

для функции f(x), заданной таблицей (2), найти много­член Р_п(х) такой, что выполняется совокупность условий интерполяции

(3)

Найти многочлен Р_п(х) — это значит, учитывая его кано­ническую форму

(4)

найти его n+ 1 коэффициент. Для этого имеется как раз n+ 1 условие (3). Таким образом, чтобы многочлен (4) был интерполяционным для функции (2), нужно, чтобы его ко­эффициенты удовлетворяли системе уравнений

Из курса алгебры известно, что определитель этой линейной сис­темы (так называемый определитель Вандермонда) отличен от нуля, т.е. решение этой системы существует и единственно. Од­нако практическое построение интерполяционного многочлена таким путем малоэффективно. Поэтому изберем другой путь.

Будем строить многочлен п-й степени L_n(x) в виде линейной комбинации многочленов п-й же степени l_i(x) (i = 0,1,..., п). Для того, чтобы такой многочлен был интер­поляционным для функции f (x), достаточно зафиксировать в качестве коэффициентов с_i, этой линейной комбинации заданные в табл.2 значения y_i = f(x_i), а от базисных многочленов l_i(x) потребовать выполнения условия

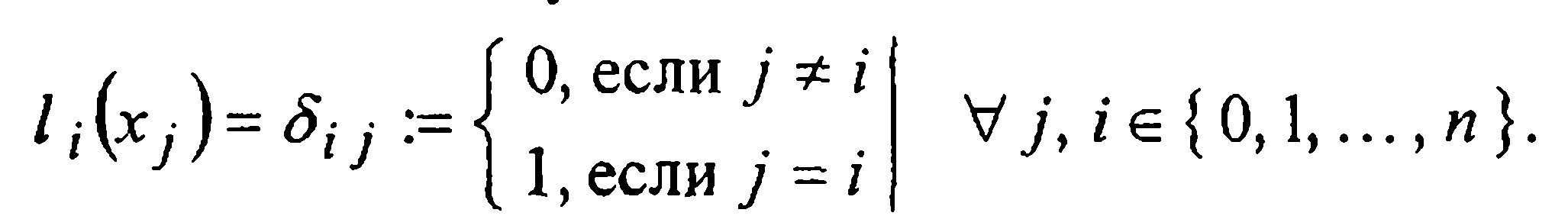(5)

В таком случае для многочлена в каждом узле x_j (j=0, 1, …, п), в силу (5), справедливо.

т.е. выполняются условия интерполяции (3).

Чтобы конкретизировать базисные многочлены l_i(x), уч­тем, что они должны удовлетворять условиям (5). Равенство нулю i -го многочлена во всех узлах, кроме i -го, означает, что l_i(x) можно записать в виде

а коэффициент А_i этого представления легко получается из со­держащегося в (5) требования l_i(x) =1. Подставляя в выраже­ние l_i(x) значение х=х_i и приравнивая результат единице, по­лучаем

Таким образом, базисные многочлены Лагранжа имеют вид

а искомый интерполяционный многочлен Лагранжа есть

(6)

Пример. Рассмотрим квадратичную интерполяцию функции y=sinx на отрезке [0, π/2] по ее трем значениям: sin0 = 0, sinπ/4= 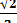, sinπ/2=1.

По формуле (8) строим многочлен Лагранжа второй степени

или после преобразований

Подставим в полученный интерполяционный многочлен кон­трольную точку Получим приближенное значение отличающееся от значения sinπ/6= 0.5 на величину ≈0.017.

Интерполяционная схема Эйткена

Пусть функция f(x) и расположение узлов x₀, x₁,..., x_n на отрезке интерпо­ляции [a, b] таковы, что имеет место сходимость процесса интерполяции. Пусть требуется найти не общее выражение L_n(x), а лишь его значения при конкретных x, т.е. решается частная задача вычисления отдельных приближенных значений функции f(x) с помощью вычисления соот­ветствующих им значений интерполяционного многочлена Лагранжа L_n(x). Для построения эффективного способа решения такой частной задачи интерполя­ции учтем следующее:

1) использование многочлена Лагранжа в виде (6) неудобно из-за его гро­моздкости, что ведет к большим вычислительным затратам;

2) заранее не известно, многочлены какой степени нужно использовать для ин­терполирования данной функции с требуемой точностью. А постепенное улучшение точности за счет вычислений L_n(x) с большим показателем степе­ни n невыгодно, т.к. L_n-1(x) плохо перестраивается в L_n(x);

3)функция f(x) задается таблицей своих приближенных значений. Процесс сходимости L_n(x) к f(x) при больших значениях n будет нарушен влиянием на результат исходных ошибок.

Построим вычислительную схему для получения приближенного значе­ния сеточной функции f(x) в заданной точке , в основу которой будет по­ложена интерполяция Лагранжа на сетке узлов Организация вычис­лений по этой схеме будет иметь итерационный характер. Каждый шаг заклю­чается в вычислении некоторого определителя второго порядка.

Пусть даны две точки на кривой Построим функ­цию

Т.е. совпадает с интерполяционным многочленом Лагранжа первой сте­пени, построенным по двум данным точкам (сравните с 6).

Построим через определитель функцию для точек

Она тоже является многочленом Лагранжа первой степени, построенным по двум точкам

Если на кривой y=f(x) заданы три точки (x_o,y_o), (x₁, y₁), (x₂, y₂), то, исполь­зуя введенные линейные функции образуем новую функцию:

Эта функция есть многочлен второй степени, решающий задачу пара­болической интерполяции по трем точкам (x₀, y₀), (x₁,y₁), (x₂,y₂). Но такой мно­гочлен единственный, следовательно, где 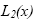- многочлен Лагранжа.

Продолжая процесс рассуждения, получим рекуррентное задание после­довательности интерполяционных многочленов Лагранжа, которое составляет суть интерполяционной схемы Эйткена:

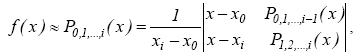(7)

где i=1, 2,…, n и по определению P₀(x)=y₀, P₁(x)=y₁.

Схема Эйткена легко реализуется на ЭВМ. Организация вычислений по формуле (7) должна быть такова, что если заранее неизвестна степень интер­поляционного многочлена, который нужно использовать для вычисления y(x), то должно происходить постепенное повышение степени k интерполирующих ее многочленов за счет подключения новых узлов. Счет ведется до тех пор, по­ка идет уточнение приближенного значения y(x).

Об этом можно судить по уменьшению величины при увеличении k и подходящем фиксировании i.

Пример. Пусть некоторая функция y=y(x) задана таблицей своих значений, округленных до двух знаков после запятой:

Рассмотрим процесс вычисления двух значений этой функции по схеме Эйткена в точках: а) б) Результаты промежуточных вычисле­ний (в которых один знак запасной) сведем в табл. 3, 4. Числа в столбцах, помеченных посредством 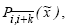представляют собой значения многочленов Лагранжа k-ой степени, построенных по узлам от i-го до (i+k)-го рекуррентно по формуле:

(8)

где k=1, 2, …, в соответствии с интерполяционной схемой Эйткена.

Порядок получения этих значений показан проставленными в каждой клетке номерами.

Таблица 3.

Вычисление по схеме Эйткена значения y(0.1)

Таблица 4.

Вычисление по схеме Эйткена значения y(0.25)

Процесс вычисления значений многочленов Лагранжа ведется до тех пор, пока идет уточнение приближенного значения т.е. уменьшается ве­личина ) при увеличении k и подходящем фиксировании i.

Например, для подсчета приближенного значения данной функции в точ­ке расположенной между узлами x_o=0.0 и x_i=0.2, целесообразно в каче­стве основной последовательности значений многочленов Лагранжа брать строку таблицы 3, соответствующую значению i=0, т.е. числа

Вычислив разности между последующими и предыдущими числами этой строки, а именно:

0.005 0.004 0.010,

видим, что дальнейший счет бессмыслен; разность перестала уменьшаться. Т.е. по данной информации о функции y(x) более точное значение y(0.1), чем y(0.1)=1.001, получаемое с помощью L₃(0.1), найти не удастся.

В случае б) вычисление по схеме Эйткена дает следующий результат: y(0.25)≈1.038, полученный с помощью L₃(0.25).

Задания: выполнить задание 1 ИДЗ№2.