Определение. Векторным полем называют часть пространства, в каждой точке которого задана некоторая векторная величина.
Векторное поле задано, если в каждой т. Р поля указан соответствующий этой точке вектор 
где P(x, y, z), Q(x, y, z), R(x, y, z) – проекции вектора на оси координат.
Векторное поле называют однородным, если P(x, y, z), Q(x, y, z), R(x, y, z) постоянные величины. Примером может служить поле тяжести.
Если вектор 
есть скорость жидкости, протекающей через поверхность σ, то поверхностный интеграл 
представляет собой общее количество жидкости, протекающей через поверхность σ за единицу времени в положительном направлении. Поверхностный интеграл называют потоком векторного поля через поверхность σ.
Поток вектора К – величина скалярная. Если изменить направление нормали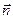 
на противоположное, т.е. переменить сторону поверхности σ, то поток К изменит знак.
Особый интерес представляет случай, когда поверхность σ замкнутая. Если берется внешняя нормаль, то мы будем говорить о потоке изнутри поверхности σ.
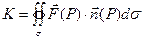
Область, которую ограничивает поверхность σ, будем называть областью V.
Величина потока К дает разность между количеством жидкости, вытекающей из области V и количеством жидкости, втекающей в эту область.
Если К=0, то в область V жидкости втекает столько же, сколько и вытекает. Так, например, будет для любой области, расположенной в потоке воды, текущей реки.
Если же величина К>0, то из области V жидкости вытекает больше, чем втекает. Это означает, что в области V имеются источники, питающие поток жидкости.
Наоборот, если величина К<0, то это указывает на наличие стоков – мест, где жидкость удаляется из потока.
