Пусть в каждой точке некоторой поверхности σ, ограниченной линией L определена функция ƒ(p). Разобьем поверхность σ произвольными кривыми на части ∆σ1, ∆σ2, ..., ∆σn. Площадь каждой из них обозначим так же
∆σ 1, ∆δ2, ..., ∆δn. Выбрав в каждой из них произвольную точку Рi составим сумму
n
∑ ƒ (Рi) ∆δi, которую называют интегральной суммой.
i=1
Предел этой суммы при max ∆σi→0 называют поверхностным интегралом первого рода и обозначают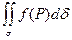 
или 
,
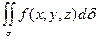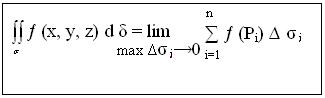при этом переменные x, y, z связаны условием: точка (x, y, z) лежит на поверхности σ.
Его вычисление сводится к вычислению двойного интеграла.
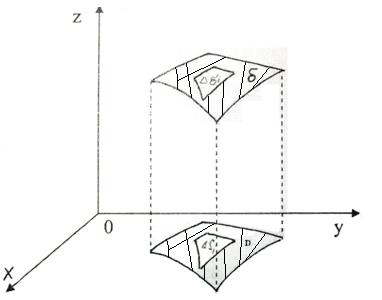
Поверхность σ задана уравнением z = z(x, y) и проектируется на плоскость xoy в области D.
Площадь поверхности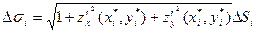 
где (xi*, yi*) – некоторая точка, лежащая в области D (т.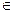 
∆Si)
где ∆Si – площадь площадки ∆Si.
т. P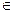i ∆ σ i
Pi = P(xi, yi, zi)
z
 |
0 y
Д
Вычисляя предел левой и правой части при max ∆σi→0 (maxΔSi→0) получим в левой части поверхностный интеграл, а в правой части двойной интеграл по области D.
|
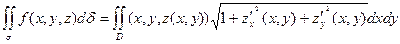
Замечание. Если поверхность σ задана уравнением: x=x(y,z) или y = y(x,z),
то поверхностные интегралы вычисляются аналогично по формулам:
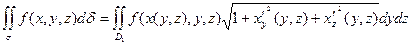
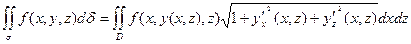
Пример (Б.3876) Вычислить 
ƒ(z + 2x + 4/3 y) dσ,
где σ – часть плоскости x/2 + y/3 + z/4 = 1, лежащая в первом октанте.
z
4 z = 4(1 – x/2 – y/3)
0 3
2 y
x
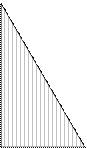
область D, т.е. ее проекция на пл. xoy
y
3
x/2 + y/3 = 1
 | |||
 | |||
0 2 x
2 3(1-x/2)
∫∫ (z + 2x + 4/3y)dδ = ∫ dx ∫ (4(1 – x/2 – y/3) + 2x + 4/3y) =
σ 0 0
2 3(1-x/2) 2 3(1-x/2) 2 2
∫ dx ∫ 4dy = 4∫ y│ dx = 4*3 ∫ (1-x/2) dx = 12(x – x3/4)│ = 12(2 – 4/4) = 12
0 0 0 0 0 0
