Рассмотрим связь между поверхностным интегралом по замкнутой поверхности σ и некоторым тройным интегралом, взятым по объему V, ограниченному этой поверхностью.
Теорема Остроградского. Если функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны вместе со своими частными производными первого порядка в области V, то имеет место формула
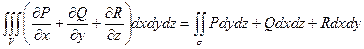
где σ – граница области V и интегрирование по σ производится по ее внешней стороне.
Эта формула называется формулой Остроградского.
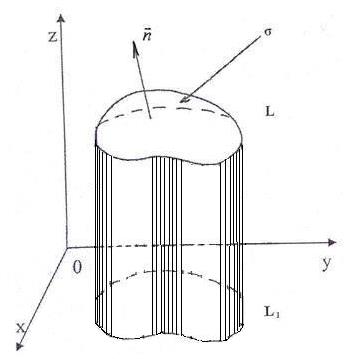
Доказательство. В пространстве oxyz задана область, ограниченная замкнутой поверхностью σ, пересекающейся любой прямой, параллельной координатным осям не более, чем в двух точках.
z Рассмотрим тройной интеграл
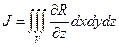
Спроектируем область V на
плоскость xoy.
Область V ограничена снизу
поверхностью z = z1(x, y, z),
0 y а сверху z = z2(x, y, z)
D
Тогда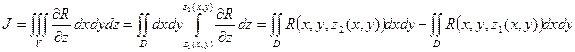 
Область D есть проекция поверхностей z = z1(x, y), z = z2(x, y) на плоскость xoy, то
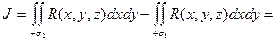(т.е. двойные интегралы численно равны поверхностным интегралам) =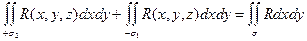 
Итак,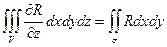 
(1)
интегрирование совершается по внешней стороне всей поверхности σ.
Аналогично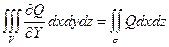 
(2)
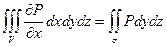(3)
Складывая почленно равенства (1), (2) и (3) получим формулу Остроградского.
Пример. Вычислить
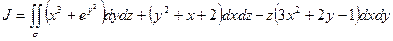
σ – внешняя сторона куба со стороной а, произвольным образом расположенная в пространстве.
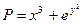
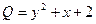
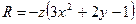
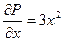
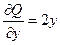
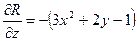
По формуле Остроградского
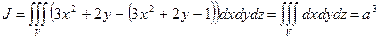
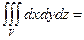формула объема области V
