Рассмотрим векторное поле 
Возьмем в этом поле некоторую кривую L.
- вектор, имеющий направление касательной к
линии L.
Тогда 
(1)
выражает работу при перемещении материальной точки вдоль линии L.
Если 
- произвольное векторное поле, а L – замкнутый контур, то интеграл (1) носит специальное название – циркуляция вектора.
Определение. Циркуляцией вектора вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора на вектор 
касательной к контуру.
Установим физический смысл циркуляции вектора в случае, когда - поле скоростей текучей жидкости.
Пусть контур L – окружность, расположенная в некоторой плоскости. Предположим, окружность является периферией колесика с радикальными лопатками, могущего вращаться вокруг оси, проходящей через его центр перпендикулярно к его плоскости.
Если циркуляция = 0, то колесико будет оставаться неподвижным: силы, действующие на лопатки, уравновешивают друг друга.
Если циркуляция 
0, то колесико будет вращаться, причем тем быстрее, чем больше величина циркуляции.
В случае произвольного векторного поля отношение циркуляции по плоскому контуру L к площади S, ограниченной этим контуром будет величиной переменной.
Вычислим 
По формуле Стокса
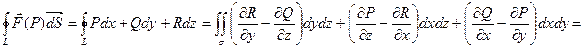
где cos α, cos β, cos γ – направляющие косинусы нормали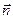 
, а σ – область, ограниченная контуром L. Последний интеграл по теореме о среднем равен произведению подинтегральной функции в некоторой т. Р1 обл. σ на величину S площади этой области.
Тогда 
,
где значения всех частных производных берутся в т. Р.
Правая часть представляет скалярное произведение 2х векторов:
единичного вектора 
- нормали к плоскости, в которой лежит контур L, и вектора, проекции которого равны
, 
, 
.
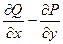Последний вектор называют ротором или вихрем векторного поля и обозначают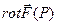 
|
Тогда формула Стокса принимает вид
Поток ротора поля через поверхность σ равен циркуляции вектора по границе этой поверхности.
Свойства ротора:
1) 
,
где С1, С2 – постоянные
2) 
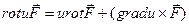
где u = u(P) – скалярная функция
- векторная функция
Доказать самостоятельно.
Пример. Найти ротор поля 
P = x2yz3 Q = -2x2yz3 R = 3x2yz3
