Градиент

Рассмотрим формулу производной скалярной функции u по направлению λ

Вторые множители являются проекциями единичного вектора , направленного по лучу λ.

Возьмем вектор, проекциями которого на оси координат будут значения частных производных в выбранной т. Р(x, y, z).

Этот вектор называют градиентом функции u (x, y, z) и обозначают graduили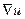

Определение. Градиентом функции u(x, y, z) называют вектор, проекциями которого служат значения частных производных этой функции, т.е.

 

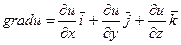
Проекции градиента зависят от выбора т. Р(x, y, z) и изменяются с изменением координат этой точки.

Каждой точке скалярного поля u (x, y, z) соответствует определенный вектор – градиент этой функции.

Итак, производная по направлению может иметь вид:

 

Производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления.

Раскрывая скалярное произведение, получим

,

 

 

где φ – угол между вектором gradu и лучом λ.

 

 

достигает наибольшего значения

при φ = 0

 

 

Итак, есть наибольшее значение производной в данной т.Р, а направление grad u совпадает с направлением луча, выходящего из т.Р, вдоль которого функция меняется быстрее всего.

Установим связь между направлением градиента функции и поверхностями уровня скалярного поля.

Теорема. Градиент функции u (x,y,z) в каждой точке совпадает с нормалью к поверхности уровня скалярного поля, проходящей через эту точку.

Доказательство. Выберем произвольную т. Р₀ (x_0, y₀, z₀).

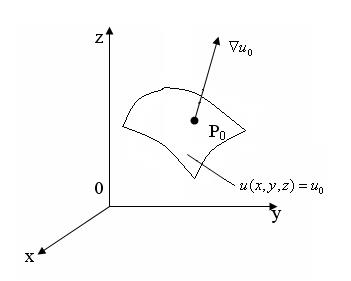Уравнение поверхности

уровня, проходящей через

т. будет u(x,y,z)= ,

u₀ = u (x₀, y₀, z₀)

 

Уравнение нормали к этой поверхности в т. , будет

Отсюда и следует, что направляющий вектор нормали, имеющий проекции , является градиентом функции u (x, y, z) в т. Р₀, ч.т.д.

Таким образом, градиент в каждой точке перпендикулярен касательной плоскости к поверхности уровня, проходящей через данную точку, т.е. его проекция на эту плоскость равна нулю.

Следовательно: Производная по любому направлению, касательному к поверхности уровня, проходящей через данную точку, равна нулю.

Основные свойства градиента функции:

1) grad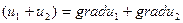

2) grad , где С – Const

3) grad

4) grad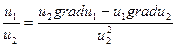

5) grad

Все свойства доказываются, используя определение градиента функции.

 

Пример. В т. М(1, 1, 1) найти направление наибольшего изменения скалярного поля и величину этого изменения.

Направление наибольшего изменения функции в точке совпадает с направлением градиента в этой точке.

 

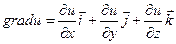
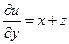
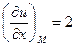
Величина этого изменения равна модулю градиента