Рассмотрим некоторую т. Р векторного поля 
и окружим ее замкнутой поверхностью σ, целиком содержащемся в поле.
Вычислим поток вектора через поверхность σ и возьмем отношение этого потока к объему V области V, ограниченной поверхностью σ:
При К>0 это отношение определяет среднюю объемную мощность источника, если поток изнутри поверхности σ меньше нуля, то говорят о мощности стока.
Найдем предел отношения при условии, что область V стягивается в т. Р, т.е. 
Если этот предел положителен, то т. Р называется источником,
а если отрицателен, то стоком.
Сама величина предела характеризует мощность источника или стока. Предел этот называют дивергенцией или расходимостью векторного поля в
т. Р.
Определение. Дивергенцией, или расходимостью векторного поля в т. Р называется предел отношения потока вектора через поверхность, окружающую т. Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в т. Р.
Обозначают 
|
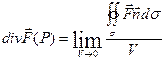
Теорема. Дивергенция векторного поля
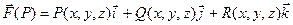
выражается формулой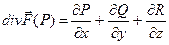 
,
где значения частных производных берутся в т. Р.
Доказательство. По формуле Остроградского
Тройной интеграл по теореме о среднем будет равен
,
где Р1 – некоторая точка области V, V – объем этой области
|
|
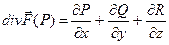
Теорему Остроградского можно записать так:
Теорему можно сформулировать так:
Поток вектора изнутри замкнутой поверхности равен тройному интегралу по объему, ограниченному этой поверхностью от дивергенции поля.
Свойства дивергенции:
1) div 
,
Где С1, С2 – Const
2) Пусть - векторное поле, u(P) – скалярное поле
div 
Доказать самостоятельно.
Пример. Найти дивергенцию поля
в т. М(1, 2, 3)
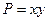
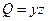
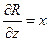
div 
