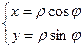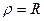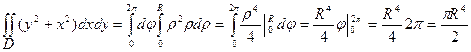Формула Грина

Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области.

Пусть в плоскости xoy задана правильная в направлении оси oy

область D.

D: x = a, x = b, причем a < b

y=y₁(x), y=y₂(x) y₁(x) ≤ y₂(x)

 

В области D заданы непрерывные функции P(x, y), Q(x, y), имеющие непрерывные частные производные.

Рассмотрим интеграл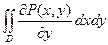

Представим его в виде двукратного

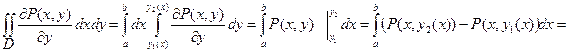
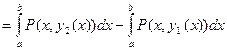(1)

(2)

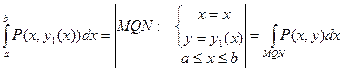(3)

 

Подставляя равенства (2) и (3) в равенство (1) получим:

 

т.е. (4)

 

Аналогично 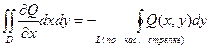(5)

 

Вычитая из (4) равенство (5) получим

 

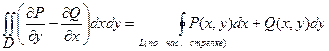
Меняя направление интегрирования, получим

 

Это и есть формула Грина (английский физик и математик)

Пример (Б.3822) Вычислить ,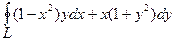

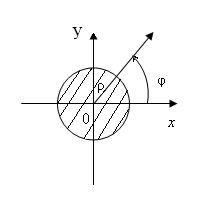где L: .

Воспользуемся формулой Грина

P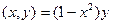

 

 

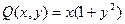
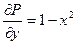
Вычислим полученный двойной нтеграл в полярных координатах

L: