49. Вычислить циркуляцию вектора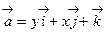 
вдоль окружности x2+y2= 1, z= 0 в положительном направлении.
Решение. В этом случае P=y; Q=x; R= 1. Следовательно,
по формуле Стокса
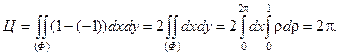
Применяя формулу Стокса, вычислить интегралы:
50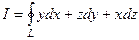 
, где L - окружность x2+y2+z2 a2, x+y+z= 0, пробегаемая против хода часовой стрелки, если смотреть с положительной оси Ox.
Решение. Применив формулу Стокса и взяв в ней в качестве поверхности Ф круг радиуса а, лежащий в плоскости x+y+z= 0, получаем:
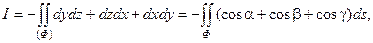
где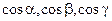 
- направляющие косинусы нормали к поверхности Ф – плоскости x+y+z= 0, так как нормаль этой плоскости образует с положительным направлением оси Oz острый угол, то в каждой из формул для вычисления 
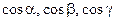перед знаком радикала возьмем знак "+".
Очевидно,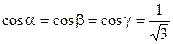 
, в силу чего имеем:
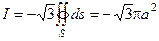
Ответ: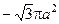 
51. 
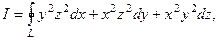L - замкнутая кривая x=a cos t, y=a cos2 t, z=a cos3 t, пробегается в направлении возрастания параметра t.
Решение. При изменении t от 0 до p подвижная точка М(x,y,z) пробегает кривую L от точки M0(a,a,a) до точки M1(-a,a,-a), а при изменении t от p до 2p точка М пробегает ту же самую часть кривой L в противоположном направлении – от точки М, до точки М0. Таким образом, точки замкнутой кривой L взаимно накладываются и кривая L не ограничивает никакой поверхности, вследствие чего I =0.
Ответ: 0.
